1 引言
共轭梯度法是求解大规模无约束优化问题
当采用精确线性搜索并且目标函数为二次凸函数时, 以上四种共轭梯度法是等价的.然而不采用精确线搜索或者目标函数为一般函数时, 这四种方法的理论结果和数值效果各不相同, 其中分子为
得出
为了保证PRP公式非负, Wei、Yao和Liu在文献[8]提出了PRP方法的一个变型, 称为WYL方法或者VPRP方法, 其中调整参数
Zhang[15]提出了一个基于PRP的三项共轭梯度法, 称为MPRP方法, 其公式如下
其中, 步长
文献[21]提出了一类新的WYL型三项共轭梯度法, 称为MWYL方法, 其公式如下
参数
受此启发, 下面给出一个新的WYL型三项共轭梯度算法并利用Zhang[15]的线搜索方式(1.1), 算法公式为
其中步长
本文组织如下:第一部分引言介绍了本文提出算法的思路; 接下来第二部分将介绍算法的流程以及证明算法是充分下降的; 第三部分证明算法在修改的Armijo线搜索条件下是全局收敛的; 第四部分对算法进行数值实验, 并与四个相关的经典算法进行比较.
2 算法
本文所提的新方法描述如下:
步骤0 选定初始步
步骤1 计算
步骤2 按照(1.1)式计算步长
步骤3 计算
为表示方便, 记为算法1.此外, 关于方向
引理2.1 若
证 当
由算法1的定义知, 当
否则
引理2.1得证, 表明算法1在不依赖于任何搜索方式下满足充分下降条件.
3 算法的收敛性分析
本节分析算法的收敛性, 首先给出相关的引理.
引理3.1 如果
证 由引理2.1看出算法1的搜索方向是充分下降的.此外, 从(1.1)式可以看出函数值序列
因此有
引理3.1证毕.
为证明算法1的全局收敛性, 首先做出如下必要假设
(
(
由于
引理3.2 若存在
从而存在一个常数
证 根据
因为
因此, 对于任意的
令
故(3.5)式成立.证毕.
现在我们给出算法1的全局收敛性.
定理3.1 若假设
证 反证法.假设结论不成立, 因此存在一个常数
如果
根据算法1中的步骤2, 当
再利用中值定理, 以及引理3.2, (2.1)、(2.2)以及(3.2)式, 存在
将上面的不等式代入(3.8)式, 故当
因为
4 数值实验
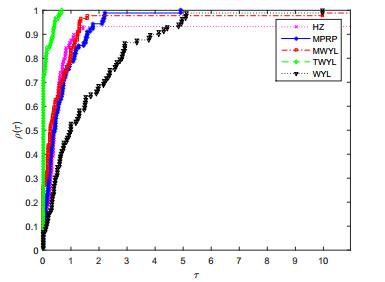
本节展示算法的数值结果.在文献[22]中选取了29个函数, 分别比较了该文所参考的MPRP方法、WYL方法、MWYL方法、同类经典的HZ方法[23]和提出的TWYL方法的数值性能.其中MPRP、TWYL方法采用修改的Armijo线搜索(1.3), WYL、MWYL采用强Wolfe线搜索, HZ采用修改的Wolfe线搜索求步长.测试环境为Win10操作系统, Intel(R) Core(TM) i7-9750H CPU 2.60GHZ 16.0GB内存.强Wolfe线搜索相关参数:
(1)
(2)
表 1给出了29个测试函数的编号及名称.
表 1 测试函数编号及名称
| Number | Function Name | Number | Function Name | Number | Function Name |
| 1 | Extended Quadratic Penaltyb QP1 | 2 | Extended Penaltyb | 3 | Extended Wood |
| 4 | Diagonal 1 | 5 | Perturbed Quadratic | 6 | Diagonal 3 |
| 7 | Generalized Tridiagonal 1 | 8 | Diagonal 4 | 9 | Diagonal 5 |
| 10 | Extended Himmelblau | 11 | Extended PSC1 | 12 | Extended BD1 (Block Diagonal) |
| 13 | Quadratic QF1 | 14 | Quadratic QF2 | 15 | Extended quadratic exponential EP1 |
| 16 | Extended Tridiagonal 2 | 17 | QUARTC (CUTE) | 18 | Partial Perturbed Quadratic |
| 19 | Almost Perturbed Quadratic | 20 | Staircase 1 | 21 | Diagonal 7 |
| 22 | Diagonal 8 | 23 | Diagonal 9 | 24 | Generalized Quartic |
| 25 | Full Hessian FH3 | 26 | SINCOS | 27 | COSINE (CUTE) |
| 28 | Raydan 1 | 29 | Hager |
图 1
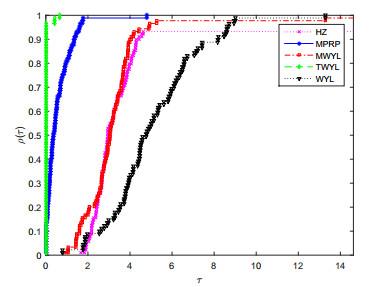
图 2
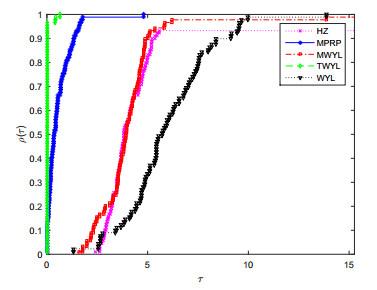
图 3
图 4
表 2表示的是MPRP方法、WYL方法、MWYL方法、TWYL方法、HZ方法对算法迭代次数
表 2 数值结果
| N | D | MPRP | WYL | MWYL | HZ | TWYL |
| 1 | 10 | 23/24/24/0.0040 | 99/1059/3218/0.0191 | 13/106/198/0.0053 | 20/110/197/0.0099 | 16/17/17/0.0019 |
| 600 | 21/22/22/0.0120 | 73/1151/2228/0.0342 | 18/100/181/0.0073 | 15/98/178/0.0172 | 11/12/12/0.0071 | |
| 1000 | 15/16/16/0.0047 | 61/933/1804/0.0348 | 18/100/181/0.0049 | 13/86/156/0.0154 | 12/13/13/0.0042 | |
| 2 | 5 | 28/29/29/0.0016 | 29/267/504/0.0029 | 34/140/245/0.0018 | 25/129/230/0.0092 | 19/20/20/0.0012 |
| 20 | 30/31/31/0.0024 | 91/1606/3120/0.0158 | 24/185/345/0.0023 | 24/149/271/0.0102 | 20/21/21/0.0016 | |
| 100 | 46/47/47/0.0061 | 26/254/481/0.0059 | 25/210/394/0.0052 | 21/166/308/0.0095 | 21/22/22/0.0037 | |
| 3 | 100 | 264/265/265/0.0051 | 5768/83377/16098/0.1955 | 270/2520/4769/0.0075 | 322/3115/5905/0.0416 | 169/170/170/0.0040 |
| 500 | 220/221/221/0.0140 | 2154/28471/54787/0.2580 | 426/3895/7363/0.0377 | 525/5062/9596/0.0865 | 213/214/214/0.0141 | |
| 1000 | 264/265/265/0.0298 | 7223/96621/186018/1.5034 | 381/3500/6618/0.0566 | 440/4268/8093/0.0871 | 251/252/252/0.0288 | |
| 4 | 10 | 30/31/31/8.4960e-4 | 37/320/602/0.0013 | 26/144/261/8.5290e-4 | 32/145/255/0.0074 | 22/23/23/6.8260e-4 |
| 100 | 47/48/48/0.0033 | 210/2749/5287/0.0257 | 46/342/637/0.0045 | 50/341/629/0.0145 | 40/41/41/0.0031 | |
| 1000 | 65/66/66/0.0505 | 84/968/1851/0.0765 | 70/601/1251/0.0521 | 93/898/1700/0.0721 | 64/65/65/0.0412 | |
| 5 | 10 | 39/40/40/0.0012 | 87/1845/3602/0.0035 | 37/174/310/7.8290e-4 | 44/233/419/0.0093 | 31/32/32/7.1240e-4 |
| 100 | 128/129/129/0.0026 | 134/1393/2651/0.0046 | 115/851/1586/0.0031 | 131/999/1864/0.0224 | 102/103/103/0.0020 | |
| 1000 | 368/369/369/0.0483 | 480/7022/13563/0.1182 | 402/4059/7715/0.0697 | 545/5637/10726/0.1131 | 337/338/338/0.0465 | |
| 6 | 10 | 33/34/34/0.0014 | 28/205/381/0.0017 | 39/159/278/0.0016 | 28/130/229/0.0063 | 20/21/21/0.0012 |
| 100 | 65/66/66/0.0058 | 69/603/1136/0.0095 | 41/272/502/0.0051 | 68/470/869/0.0206 | 45/46/46/0.0044 | |
| 1000 | 80/81/81/0.0667 | 86/1026/1965/0.1169 | 66/615/1136/0.0704 | 78/756/1431/0.0744 | 71/72/72/0.0616 | |
| 7 | 10 | 53/54/54/0.0032 | 32/303/573/0.0039 | 34/195/355/0.0033 | 31/190/346/0.0073 | 30/31/31/0.0020 |
| 100 | 40/41/41/0.0062 | 400/7132/13863/0.4381 | 31/184/336/0.0069 | 27/164/298/0.0078 | 23/24/24/0.0034 | |
| 1000 | 27/28/28/0.0104 | 30/329/627/0.0292 | 42/241/439/0.0250 | 23/140/254/0.0188 | 19/20/20/0.0078 | |
| 10000 | 23/24/24/0.0718 | 275/5356/10436/4.7556 | 26/150/273/0.1357 | 18/111/201/0.0889 | 14/15/15/0.0452 | |
| 20000 | 23/24/24/0.1684 | 28/310/591/0.5345 | 26/148/269/0.2359 | 16/97/175/0.1371 | 12/13/13/0.0840 | |
| 8 | 10 | 38/39/39/8.1400e-4 | 1171/15199/29226/0.0249 | 74/470/865/0.0013 | 50/359/665/0.0082 | 51/52/52/7.4680e-4 |
| 500 | 42/43/43/0.0021 | 1315/16667/32018/0.0818 | 63/398/732/0.0024 | 54/389/721/0.0062 | 57/58/58/0.0018 | |
| 1000 | 39/40/40/0.0033 | 1341/16869/32396/0.2188 | 70/442/813/0.0064 | 82/584/1083/0.0117 | 62/63/63/0.0048 | |
| 9 | 10 | 3/4/4/0.0011 | 3/7/10/0.0011 | 5/11/16/9.2270e-4 | 7/22/34/0.0016 | 3/4/4/8.9320e-4 |
| 100 | 3/4/4/0.0013 | 3/7/10/0.0010 | 5/11/16/0.0013 | 6/19/29/0.0021 | 3/4/4/0.0010 | |
| 10 | 10 | 48/49/49/0.0017 | 42/665/1287/0.0029 | 54/363/671/0.0020 | 22/165/305/0.0077 | 23/24/24/0.0012 |
| 100 | 52/53/53/0.0020 | 46/728/1409/0.0037 | 57/383/708/0.0026 | 31/230/426/0.0045 | 23/24/24/0.0013 | |
| 1000 | 56/57/57/0.0054 | 48/758/1467/0.0134 | 58/390/721/0.0074 | 27/199/368/0.0054 | 25/26/26/0.0030 | |
| 10000 | 56/57/57/0.0579 | 52/815/1577/0.1831 | 58/390/721/0.1078 | 31/232/430/0.0928 | 29/30/30/0.0517 | |
| 11 | 10 | 16/17/17/0.0014 | 15/58/100/0.0013 | 30/139/247/0.0018 | 18/79/137/0.0034 | 16/17/17/0.0011 |
| 100 | 15/16/16/0.0016 | 15/58/100/0.0014 | 29/134/238/0.0022 | 16/72/125/0.0039 | 15/16/16/0.0014 | |
| 1000 | 15/16/16/0.0039 | 13/51/88/0.0041 | 28/130/231/0.0085 | 16/72/125/0.0052 | 14/15/15/0.0035 | |
| 12 | 10 | 37/38/38/9.3410e-4 | 61/1124/2186/0.0035 | 27/119/210/0.0018 | 28/145/259/0.0046 | 27/28/28/8.0080e-4 |
| 100 | 39/40/40/0.0013 | 65/1175/2284/0.0051 | 27/119/210/0.0012 | 30/156/279/0.0052 | 28/29/29/9.8960e-4 | |
| 1000 | 39/40/40/0.0038 | 69/1223/2376/0.0261 | 28/124/219/0.0034 | 32/166/297/0.0093 | 30/31/31/0.0033 | |
| 13 | 1000 | 376/377/377/0.0308 | 468/5435/10401/0.0547 | 454/4196/7937/0.0429 | 462/4369/8273/0.1338 | 307/308/308/0.0249 |
| 10000 | 1316/1317/1317/3.1568 | 1620/24780/47939/5.6254 | 2791/33598/64404/8.2298 | 1663/20450/39234/7.6030 | 1135/1136/1136/1.6381 | |
| 20000 | 2089/2090/2090/5.7360 | 3224/56220/109215/16.2122 | 4791/61853/118914/18.7639 | 2321/30644/58964/22.2503 | 1613/1614/1614/4.8625 | |
| 14 | 10 | 54/55/55/0.0011 | 121/1623/3124/0.0038 | 38/219/399/0.0013 | 42/257/469/0.0075 | 32/33/33/8.5090e-4 |
| 600 | 321/322/322/0.0206 | 5682/137079/268475/1.1904 | 327/3383/6438/0.0317 | 392/4137/7879/0.0521 | 265/266/266/0.0185 | |
| 1000 | 396/397/397/0.0399 | 501/7736/14970/0.0992 | 469/5196/9922/0.0701 | 518/5796/11071/0.0852 | 348/349/349/0.0378 | |
| 15 | 10 | 60/61/61/0.0019 | 81/1739/3396/0.0056 | 13/115/216/9.7820e-4 | 23/231/436/0.0053 | 17/18/18/8.4180e-4 |
| 100 | 55/56/56/0.0030 | 73/1587/3100/0.0104 | 12/106/199/0.0019 | 21/211/398/0.0052 | 16/17/17/0.0017 | |
| 1000 | 49/50/50/0.0122 | 65/1426/2786/0.0520 | 11/97/182/0.0040 | 17/171/322/0.0070 | 16/17/17/0.0043 | |
| 16 | 1000 | 42/43/43/0.0042 | 33/167/300/0.0062 | 26/86/145/0.0037 | 36/142/245/0.0076 | 26/27/27/0.0034 |
| 10000 | 36/37/37/0.0337 | 15/127/238/0.0404 | 12/43/73/0.0176 | 14/61/105/0.0233 | 15/16/16/0.0210 | |
| 20000 | 32/33/33/0.0580 | 12/76/139/0.0512 | 11/40/68/0.0270 | 10/47/81/0.0316 | 10/11/11/0.0240 | |
| 100000 | 24/25/25/0.1614 | 9/58/106/0.1309 | 9/33/56/0.0811 | 7/36/62/0.0756 | 9/10/10/0.0670 | |
| 17 | 1000 | 1/2/2/0.0149 | 1000/20044/30088/9.3673 | 1000/20001/30002/9.2210 | -/-/-/- | 1/2/2/0.0068 |
| 18 | 10 | 35/36/36/0.0033 | 93/2021/3948/0.0291 | 27/136/244/0.0029 | 26/139/249/0.0066 | 24/25/25/0.0027 |
| 100 | 75/76/76/0.0359 | 80/802/1523/0.0908 | 72/540/1007/0.0594 | 86/673/1257/0.1408 | 72/73/73/0.0319 | |
| 1000 | 334/335/335/51.9645 | 348/5448/10547/98.1685 | 389/4631/8872/78.6427 | 491/5943/11392/90.9052 | 305/306/306/32.5759 | |
| 19 | 10 | 36/37/37/8.8550e-4 | 89/1945/3800/0.0081 | 33/157/280/9.2980e-4 | 43/226/406/0.0050 | 31/32/32/7.7060e-4 |
| 100 | 118/119/119/0.0059 | 142/1620/3097/0.0110 | 116/855/1593/0.0068 | 128/965/1799/0.0209 | 104/105/105/0.0051 | |
| 1000 | 365/366/366/0.0464 | 512/7484/14455/0.1206 | 400/4038/7675/0.0666 | 469/4841/9210/0.0901 | 325/326/326/0.0434 | |
| 10000 | 1140/1141/1141/2.2828 | 2024/36184/70343/7.2277 | 2630/33971/65311/6.6585 | 1606/21180/40751/7.7436 | 1115/1116/1116/2.3376 | |
| 20 | 10 | 111/112/112/0.0038 | 645/6679/12712/0.0377 | 88/550/1011/0.0041 | 120/795/1467/0.0197 | 104/105/105/0.0036 |
| 50 | 581/582/582/0.0448 | 7249/75221/143192/0.8142 | 720/7177/13633/0.0812 | 649/6657/12662/0.1175 | 526/527/527/0.0433 | |
| 100 | 1389/1390/1390/1.1858 | 1461/23309/45156/1.9609 | 1580/18355/35129/1.7259 | 1436/17161/32883/0.4488 | 1096/1097/1097/0.6747 | |
| 21 | 1000 | 23/24/24/0.0713 | 26/317/607/0.0249 | 8/24/39/0.0027 | 10/41/69/0.0167 | 12/13/13/0.0040 |
| 10000 | 30/31/31/0.0016 | 20/227/433/1.5810 | 7/21/34/0.1396 | 9/37/62/0.0854 | 9/10/10/0.1825 | |
| 20000 | 24/25/25/0.5173 | 20/226/431/3.2724 | 7/21/34/0.2893 | 9/37/62/0.1277 | 9/10/10/0.3605 | |
| 22 | 100 | 30/31/31/0.0016 | 18/183/347/0.0025 | 11/32/54/0.0011 | 12/49/83/0.0042 | 11/12/12/0.0011 |
| 10000 | 24/25/25/0.0418 | 12/106/199/0.0825 | 9/27/44/0.0197 | 10/41/69/0.0476 | 8/9/9/0.0189 | |
| 20000 | 23/24/24/0.0713 | 10/83/155/0.1243 | 9/27/44/0.0377 | 10/41/69/0.0590 | 8/9/9/0.0342 | |
| 23 | 10000 | 103/104/104/0.8917 | 101/1647/3192/1.1939 | 92/1200/2307/0.9328 | 94/1242/2387/0.8362 | 91/92/92/0.7481 |
| 20000 | 59/60/60/0.8852 | 73/1302/2530/1.8032 | 68/895/1721/1.2813 | -/-/-/- | 58/59/59/0.8296 | |
| 100000 | 64/65/65/5.0643 | 108/2333/4557/15.1715 | 71/1174/2276/7.5531 | -/-/-/- | 54/55/55/4.3003 | |
| 24 | 10000 | 20/21/21/0.0138 | 137/3270/6402/0.5786 | 20/63/105/0.0138 | 30/122/211/0.0609 | 18/19/19/0.0110 |
| 15000 | 23/24/24/0.0203 | 137/3261/6384/1.0262 | 19/60/100/0.0261 | 31/124/214/0.0910 | 21/22/22/0.0210 | |
| 20000 | 22/23/23/0.0324 | 137/3253/6368/1.2361 | 19/58/96/0.0228 | 31/124/214/0.1063 | 18/19/19/0.0199 | |
| 25 | 50 | 36/37/37/0.0019 | 243/5487/10730/0.0282 | 17/113/208/0.0081 | 46/370/691/0.0127 | 18/19/19/0.0014 |
| 100 | 37/38/38/0.0200 | 103/2346/4588/0.0313 | 23/176/328/0.0025 | 30/270/507/0.0125 | 25/26/26/0.0095 | |
| 1000 | 449/450/450/0.2043 | 72/1683/3293/0.0947 | -/-/-/- | 29/345/658/0.0351 | 15/16/16/0.0153 | |
| 26 | 10000 | 14/15/15/0.0301 | 12/47/81/0.0342 | 28/130/231/0.1007 | 15/67/116/0.0788 | 12/13/13/0.0321 |
| 20000 | 14/15/15/0.0546 | 12/47/81/0.0696 | 28/129/229/0.1529 | 15/67/116/0.1037 | 11/12/12/0.0477 | |
| 100000 | 13/14/14/0.2266 | 11/44/76/0.2716 | 27/126/224/0.6975 | 11/50/86/0.2511 | 11/12/12/0.2078 | |
| 27 | 100 | 46/47/47/0.0035 | 55/656/1256/0.0103 | 25/253/480/0.0049 | -/-/-/- | 19/20/20/0.0020 |
| 1000 | 23/24/24/0.0197 | 73/1332/2590/0.1416 | 16/162/307/0.0195 | -/-/-/- | 14/15/15/0.0071 | |
| 10000 | 16/17/17/0.0686 | 106/1118/2129/1.2885 | 15/114/212/0.1380 | -/-/-/- | 15/16/16/0.0618 | |
| 28 | 10000 | 64/65/65/0.2786 | 73/808/1542/0.4350 | 48/452/855/0.2320 | 73/712/1348/0.4219 | 58/59/59/0.2042 |
| 50000 | 55/56/56/1.1709 | 159/2313/4466/4.1139 | 46/527/1007/1.3277 | 86/1025/1961/3.5063 | 40/41/41/0.8828 | |
| 100000 | 45/46/46/2.0890 | 45/735/1460/3.7004 | 49/605/1160/2.8631 | 39/488/934/3.8924 | 33/34/34/1.6141 | |
| 29 | 1000 | 30/31/31/0.0209 | 25/175/324/0.0167 | 28/147/265/0.0141 | 26/142/255/0.0237 | 22/23/23/0.0099 |
| 10000 | 21/22/22/0.1070 | 52/774/1495/0.7530 | 22/152/281/0.1586 | 21/150/276/0.1327 | 21/22/22/0.1054 | |
| 20000 | 20/21/21/0.2274 | 22/308/593/0.5727 | 19/182/344/0.3380 | 21/153/282/0.2527 | 19/20/20/0.2101 |
参考文献
Methods of conjugate gradients for solving linear systems
DOI:10.6028/jres.049.044 [本文引用: 1]
Function minimization by conjugate gradients
DOI:10.1093/comjnl/7.2.149 [本文引用: 1]
Note sur la convergence de méthodes de directions conjuguées
The conjugate gradient method in extremal problems
DOI:10.1016/0041-5553(69)90035-4 [本文引用: 1]
A nonlinear conjugate gradient method with a strong global convergence property
DOI:10.1137/S1052623497318992 [本文引用: 1]
Convergence properties of algorithms for nonlinear optimization
Global convergence properties of conjugate gradient method for optimization
The convergence properties of some new conjugate gradient methods
The proof of the sufficient descent condition of the Wei-Yao-Liu conjugate gradient method under the strong Wolfe-Powell line search
Two modified nonlinear conjugate gradient methods with disturbance factors for unconstrained optimization
Further studies on the Wei-Yao-Liu nonlinear conjugate gradient method
Some global convergence properties of the Wei-Yao-Liu conjugate gradient method with inexact line search
A note about WYLs conjugate gradient method and its application
A hybrid PRP-WYL conjugate gradient method with the strong wolfe line search
A descent modified Polak-Ribiére-Polyak conjugate gradient method and its global convergence
DOI:10.1093/imanum/drl016 [本文引用: 2]
一个三项LS共轭梯度方法
A three-term LS conjugate gradient method
Some three-term conjugate gradient methods with the new direction structure
DOI:10.1016/j.apnum.2019.10.011
A modified Hestenes-Stiefel conjugate gradient method with an optimal property
DOI:10.1080/10556788.2018.1457150
A modified three-term PRP conjugate gradient algorithm for optimization models
Two modified three-term conjugate gradient methods with sufficient descent property
DOI:10.1007/s11590-014-0736-8 [本文引用: 1]
一类新的WYL型共轭梯度法及其全局收敛性
Global convergence of a new Wei-Yao-Liu type conjugate gradient method
An unconstrained optimization test functions collection
A new conjugate gradient method with guaranteed descent and an efficient line search
DOI:10.1137/030601880 [本文引用: 1]