1 引言
设
对任意的
横截性定理[7]:令
本文的研究动机之一是要在横截性条件不成立的时候, 即
(i) 对任意的
(ii) 对任意的
以下是本文的主要定理.
定理1.1 令
2 预备知识
在这一节中, 将介绍广义逆, 广义正则值和广义横截性等基本工具.
2.1 广义逆, 局部精细点和广义正则值
研究广义横截性的重要工具之一是Banach空间中线性算子的广义逆. 记
其中
令
映射
是切映射
的表示, 其中
局部精细点[11]. 设
引理2.1[11]
引理2.2[10]
如果
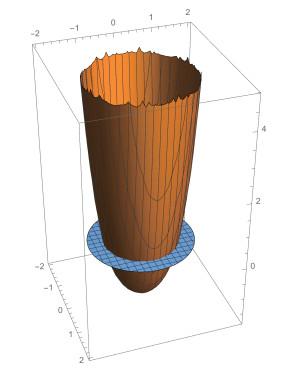
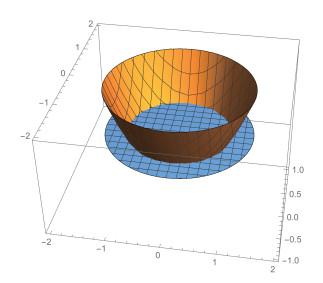
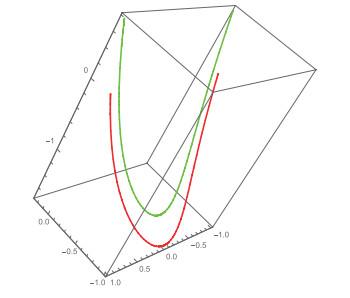
2.2 广义横截性举例
令
那么
证 由于
那么Rank
事实上,
证毕.
图 1
图 2
图 3
3 主要结果的证明
对于强临界值, Sard-Smale引理也成立.
引理3.1 设
证 强临界值集合是临界值集合的子集. 由Sard-Smale引理, 引理3.1成立.
定义3.1 映射
映射
这里
由下面的交换图(图 4)易得, Fredholm算子不依赖于容许图卡
图 4
令
显然
对任意的
其中
其中
由于
(i)
(ii)
(iii)
因此, Banach流形间的Fredholm算子的概念是合理的.
以下是本文主要定理(定理1.1)的证明.
证 令
定义嵌入映射:
事实上, 由于
对任意的
因为
其中
使得
由
所以,
由引理
若
对任意的
其中
且
根据式(3.1)与(3.2) 有
另一方面, 有
现在考虑
若
若
零空间
张成, 这意味着
即
由式(3.3)和(3.4) 有
这意味着
参考文献
Singularities of horospherical hypersurfaces of curves in hyperbolic 4-space
DOI:10.1017/S144678871100139X [本文引用: 1]
Singularities of hyperbolic Gauss maps
Bifurcations of completely integrable 2-variable first-order partial differential equations
DOI:10.1016/j.jmaa.2011.03.020 [本文引用: 1]
Bifurcation from simple eigenvalues
DOI:10.1016/0022-1236(71)90015-2 [本文引用: 1]
Bifurcation from a degenerate simple eigenvalue
DOI:10.1016/j.jfa.2013.02.010 [本文引用: 1]
A theory for imperfect bifurcation via singularity theory
论广义横截性
DOI:10.3321/j.issn:1003-3998.2007.02.020 [本文引用: 1]
On generalized transversality
DOI:10.3321/j.issn:1003-3998.2007.02.020 [本文引用: 1]
A generalized transversality in global analysis
DOI:10.2140/pjm.2008.236.357 [本文引用: 2]
A generalized preimage theorem in global analysis
DOI:10.1007/BF02878710 [本文引用: 2]