1 引言
生态环境的不断破坏和国际交流的日趋频繁是影响传染病的暴发和流行的重要因素. 近年来, 新冠肺炎和非典型肺炎等新型传染病不断暴发以及肝炎、肺结核等原有疾病的反复发作给人类的健康和社会经济的发展带来了严重威胁. 运用数学模型研究传染病的传播规律和流行趋势对疾病的预防和控制具有重要的理论和实践意义.
然而, 疾病传播过程中往往受到复杂环境中不确定因素的影响. 具有不同形式噪声干扰的传染病模型近年来受到普遍关注, 如文献[9-12]等. 赵亚男等人[9]在文献[3]的基础上对感染系数进行随机扰动并提出了一类SIVS模型, 研究发现当噪声较大时, 不论基本再生数是否小于1, 感染人群的数量都将指数衰减为0. 刘群和蒋达清[10]采取了同样的扰动方法建立了一类接种后不完全免疫的SIVS模型, 给出了疾病灭绝的条件, 且发现较大的噪声能够有效地抑制疾病的流行. 在文献[11-12]中, 赵亚男和蒋达清假设随机扰动项与易感者类(
以上论文中随机干扰项均为系统状态的线性函数, 在文献[13]中张伟伟等人使用白噪声模拟环境波动, 提出了一类具有非线性扰动的随机非自治SIRI模型, 给出了解的随机有界性、随机持久性和疾病持续存在的解析结果, 且对于具有马尔科夫转换的系统得到了遍历平稳分布和正常返存在的充分条件.
事实上, 影响疾病传播的环境噪声不仅有上述的白噪声(一种功率谱密度为常数的随机过程, 通常用布朗运动广义均方导数表示), 还有一种强度大但数量少的有色噪声, 又称为电报信号噪声[14-15]. 在现实生活中, 很多疾病的传播受季节、气候、政治人文因素的改变影响较大, 如Covid-19, SARS, 流感等. 这一类因素的功率谱密度函数不为常数, 不能单纯地用布朗运动来描述其随机性, 因此一些学者在传染病建模过程中运用Markov切换描述其随机性, 如文献[16-17]等. 本文拟运用Markov切换描述有色噪声, 建立具有非线性随机扰动及预防接种策略的传染病模型, 并通过李雅普诺夫函数、Chebyshev's不等式、Has'minskii理论、强大数定理等方法研究模型的持久性、灭绝性和遍历性等性质.
2 模型的建立
胡俊娜[18]等人提出了转换机制(环境状态之间的转换通常是无记忆的, 下一次切换停留时间服从指数分布)下具有非线性发病率的随机SIVS传染病模型
其中
其中
不难验证, 当
建立如下SIVS模型
其中
为了讨论方便, 假设
除了各种环境噪声外, 在现实中, 环境的周期变化也是影响传染病传播的一个重要因素, 基于系统(2.2), 忽略有色噪声, 我们建立如下具有周期系数的非自治传染病模型
其中所有系数均为正
为了讨论模型(2.2)-(2.3)的性质, 我们引入如下结论. 首先考虑随机微分方程
引理2.1[19] 假设系统(2.4)的系数在
ⅰ)
ⅱ)
则系统(2.4)存在
其中
为了给出状态转换下微分方程的结果, 定义如下方程
其中
引理2.2[20] 若满足以下条件
ⅰ) 对任意的
ⅱ)对于任意的
ⅲ) 存在闭包非空的开集
3 系统(2.3)的随机有界性、持久性以及非平凡正周期解的存在性
定义1[13] 若对于任意的
则称
定义2[21] 若对于任意的
则称
定义参数
定理3.1 若
证 定义
其中
意味着
因此
选取足够大的常数
意味着
可得
对于
类似地
所以
注意到
定理3.1证毕.
下面研究系统(2.3)周期解的存在性. 定义参数
定理3.2 当
证 根据定理3.1的证明可知, 对于任意的
其中
均为正常数, 且
其中
从而有
设
类似地
其中
其中
选取足够大的正常数
定义有界区域
选择足够小的正常数
为了讨论方便, 将
显然,
1) 当
2) 当
3) 当
4) 当
5) 当
6) 当
综上, 对任意的
4 平均意义下的持久性
定理4.1 当
证 根据定理3.1可知, 对于任意的
将上式两端从
其中
由
运用It
将上式从
其中
从而得
则系统(2.2)的染病者在平均意义下具有持久性.
5 遍历平稳分布
本节讨论系统(2.2)的遍历平稳分布的存在性. 为此, 定义参数
定理5.1 当
证 对
为了使引理2.2中的条件ⅲ)成立, 考虑有界开集
其中
显然引理2.2中的条件ⅱ)成立. 在
其中
其中
选取足够小的
为了给出
综上可得
运用类似定理3.2的方法可得
6 系统的灭绝性
在本节中, 给出随机系统(2.2)的染病者灭绝的条件. 定义参数
定理6.1 当
证 根据It
两边从
其中
通过指数鞅不等式, 对于任何正常数
其中
因此对于几乎所有的
对于所有的
不难看出, 对于
根据强大数定理得
从而有
7 数值模拟
本节进行数值模拟, 为此我们使用如下离散方程
选取以下参数值
经计算可得
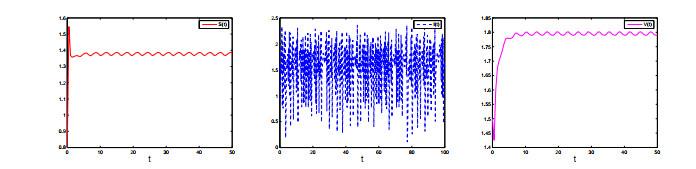
图 1
在系统(2.2)中, 我们考虑右连续的马尔科夫链
(1) 当
(2) 当
经计算可得
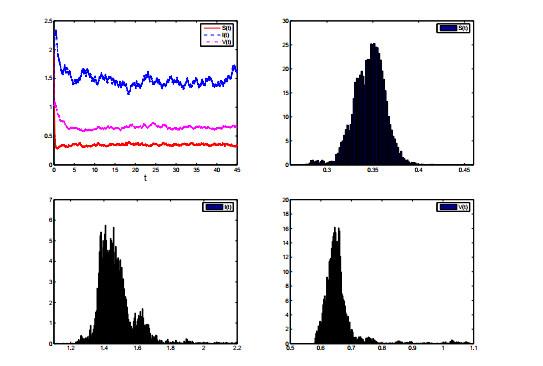
图 2
选取以下参数值.
(1) 当
(2) 当
经计算可得
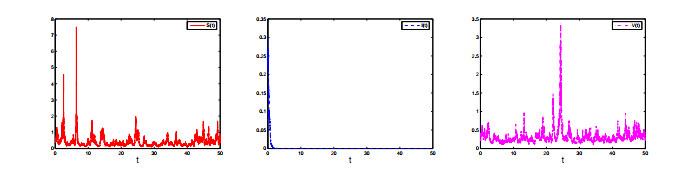
图 3
8 结论
本文考虑环境之间的随机切换建立了一类具有非线性随机扰动非自治SIVS模型. 首先忽略有色噪声的影响, 定义了模型的阈值, 证明了随机正周期解的存在性, 并进行数值模拟验证了理论结果. 表明易感人群, 感染人群及接种疫苗后获得免疫的人群的数量由于季节的变化、天气的转变等因素的影响呈周期性变化.
在有色噪声的影响下, 我们证明了模型的平均持久性、遍历性和绝灭性等. 这些数学结论的生物意义如下.
由定理4.1知当
由定理5.1知当
由定理6.1知当
参考文献
Qualitative analyses of SIS epidemic model with vaccination and varying total population size
Disease extinction and persistence in a discrete-time SIS epidemic model with vaccination and varying population size
Global analysis of SIS epidemic models with variable total population size
A simple vaccination model with multiple endemic states
DOI:10.1016/S0025-5564(00)00003-1
A qualitative study of a vaccination model with nonlinear incidence
Stability and bifurcation of an SIVS epidemic model with treatment and age of vaccination
Rich bifurcation structure in a two-patch vaccination model
Dynamic behavior analysis of SIVS epidemic models with state-dependent pulse vaccination
DOI:10.1016/j.nahs.2017.08.004 [本文引用: 1]
The extinction and persistence of the stochastic SIS epidemic model with vaccination
DOI:10.1016/j.physa.2013.06.009 [本文引用: 2]
The threshold of a stochastic SIS epidemic model with imperfect vaccination
DOI:10.1016/j.matcom.2017.06.004 [本文引用: 1]
Dynamics of stochastically perturbed SIS epidemic model with vaccination
The threshold of a stochastic SIS epidemic model with vaccination
DOI:10.1016/j.amc.2014.05.124 [本文引用: 2]
Periodic solution and ergodic stationary distribution of stochastic SIRI epidemic systems with nonlinear perturbations
DOI:10.1007/s11424-018-7348-9 [本文引用: 2]
Evolution of predator-prey systems described by a Lotka-Volterra equation under random environment
Conditions for persistence and ergodicity of a stochastic Lotka-Volterra predator-prey model with regime switching
Stochastic SIR model with jumps
DOI:10.1016/j.aml.2013.03.013 [本文引用: 1]
Asymptotic properties of hybrid diffusion systems
DOI:10.1137/060649343 [本文引用: 1]
Global stability and stochastic permanence of a non-autonomous logistic equation with random perturbation
DOI:10.1016/j.jmaa.2007.08.014 [本文引用: 1]