1 引言
其中
(H1) 当病原体密度特别高时, 特异性免疫细胞的复制率要高于其衰减率, 即
(H2) 在高密度病原体的免疫反应过程中, 特异性免疫强于非特异性免疫, 即
由上面两条假设可知, 对应模型(1.1)的简化模型(1.2)的参数就满足
近年来, 许多研究表明, 侵入到宿主血液或体液的细菌、病毒和寄生虫, 会随着血液或体液的流动而移动(或扩散)到其他部位, 导致病原体感染宿主体内的一些组织器官, 如HCV通过血液流动而进入肝脏导致丙肝或肝癌[9], 某些病毒可能还会扩散到全身(如HIV[10]), 有些细菌进入血液, 还能引起的菌血症[11]; 寄生虫(盾纤毛虫)进入鱼类体内, 会引起白点病和白斑病[12-13], HBV可引起的乙型肝炎[14]、蚊子的叮咬可以传播的疟疾[15] 和登革热[16], 埃博拉病毒可引起出血热[17]等等. 这些疾病的爆发均与病原体侵入生物体, 并在血液、体液或体内扩散有密切联系. 因此, 研究扩散因素对血液或体液中病原体与免疫细胞相互作用的影响是非常有必要的.
这里
下面研究当病原体与免疫细胞相互作用时, 扩散效应和免疫滞后对模型(1.4)稳态解的稳定性以及该模型周期解存在性的影响, 即模型经历Turing分支和Hopf分支的情况.
2 扩散因素与时滞因素对稳态解稳定性的影响
众所周知, 扩散项与时滞项的引入不影响平衡解的存在性. 由文献[8]可推知, 模型(1.4)总是存在一个无病原体稳态解
下面来讨论模型(1.4)稳态解
2.1 扩散因素与时滞因素对无病原体稳态解稳定性的影响
经理论分析, 可得到扩散项与时滞项对无病原体稳态解
定理2.1 当
证 模型(1.4)在无病原体稳态解
代入方程(2.1)可得到一列特征方程
其中每个特征方程都有两个特征根
由
2.2 扩散因素与时滞因素对正稳态解稳定性的影响
参考文献[8]的理论结果可得, 当
引理2.1[8] 当
由文献[8]中的理论结果可知
与分析稳态解
代入模型(1.4)正稳态解
其中
下面从特征方程(2.4)根的分布出发, 来讨论扩散和时滞对正稳态解
令
由引理2.1可知, 当
引理2.2 如果方程(1.4)在
这里,
证 本部分证明参考了文献[24]的证明思路. 当
经计算可得, 如果
引理2.2给出了模型(1.4)经历Turing分支的可行域, 下面进一步来确定当
其中
引理2.3 假设
而且当
那么, 对
由引理2.2和引理2.3可得如下引理.
引理2.4 对于给定的正整数
证 当
其中,
下面证明不等式(2.16), 将特征方程(2.4)的两边对
由隐函数求导定理可得
引理结论成立. 证毕.
由引理2.4, 可得到扩散因素对模型(1.4)正稳态解
定理2.2 假设
上面得到了扩散因素对正稳态解稳定性的影响, 下面讨论免疫时滞对正平衡解稳定性的影响. 在
分离实部和虚部可得
由(2.17)式, 可得
将(2.18) 式两边平方相加可得
为了讨论方便, 令
由求根公式, 可得(2.21)式的解为
由
引理2.5 如果
证 首先, 判断(2.22) 式中
此时由(2.22)式可知, 只有当
由(2.24)式可知, 当
当
综上, 因对于任意
由引理2.5, (2.21)式与(2.22)式可得, 当
再将
此时
当
因此有
引理2.6 如果
证 由(2.4)式可知
利用隐函数求导定理, 则有
进一步得出
横截条件成立. 证毕.
由定理2.2和引理2.6可得如下定理.
定理2.3 如果
3 数值模拟
本部分中, 参考文献[8] 中模型的参数, 首先, 选取如下参数进行数值模拟.
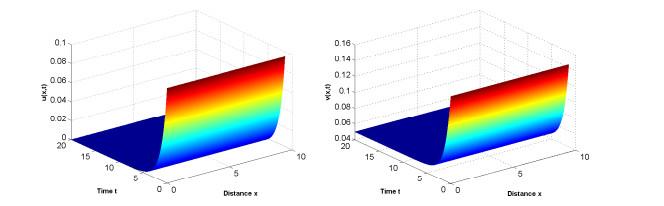
此时, 由
图 1
图 1
参数为(3.1),
此时, 由
图 2
图 3
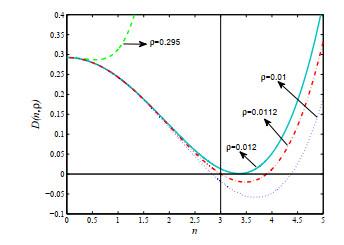
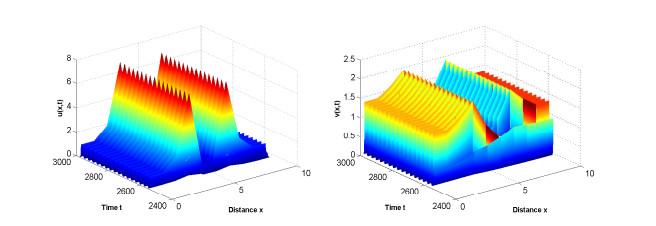
由图 2可见, 当
图 4
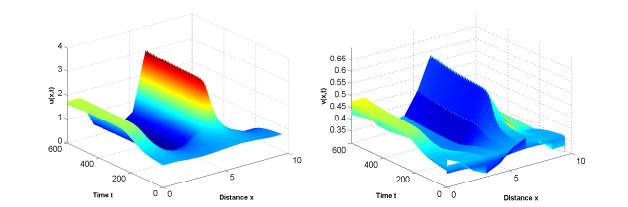
若选取
图 5
图 6
图 6
参数为(3.2),
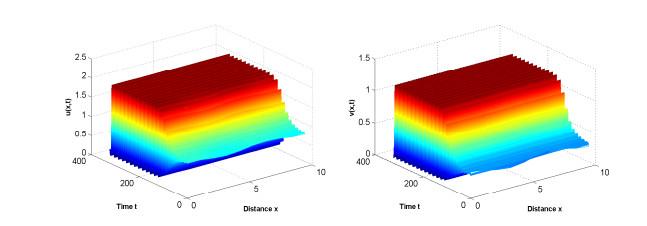
此外, 选取
图 7
图 7
参数为(3.2),
4 结论
本文研究了具时滞扩散效应的病原体-免疫模型稳态解的稳定性以及在稳态解处经历Turing分支和Hopf分支的条件. 从理论分析中得到, 如果病原体繁殖率
另外, 从正稳态解的稳定性理论分析和数值模拟中, 可以得到当病原体扩散速度远小于免疫细胞扩散速度, 即扩散比率
参考文献
Numerical study of SARS epidemic model with the inclusion of diffusion in the system
A review of mathematical models of influenza a infections within a host or cell culture: lessons learned and challenges ahead
DOI:10.1186/1471-2458-11-S1-S7
流行性病毒传播生态动力学系统
DOI:10.3969/j.issn.1003-3998.2019.01.019
Bionomics dynamic system for epidemic virus transmission
DOI:10.3969/j.issn.1003-3998.2019.01.019
新型冠状病毒肺炎疫情数据挖掘与离散随机传播动力学模型分析
Analysis of COVID-19 epidemic traced data and stochastic discrete transmission dynamic model
封闭空间中新型冠状病毒肺炎传播模型: 以日本"钻石公主号"邮轮为例
DOI:10.3969/j.issn.1003-3998.2020.02.024
COVID-19 transmission model in an enclosed space: a case study of Japan Diamond Princess Cruises
DOI:10.3969/j.issn.1003-3998.2020.02.024
Modeling host-parasite coevolution: a nested approach based on mechanistic models
DOI:10.1006/jtbi.2002.3076 [本文引用: 2]
Transient dynamics and early diagnostics in infectious disease
DOI:10.1007/s002850100103 [本文引用: 1]
A simple model of pathogen-immune dynamics including specific and non-specific immunity
Hepatitis C virus infection is blocked by HMGB1: a new nonlocal and time-delayed reaction-diffusion model
Turing patterns from dynamics of early HIV infection
DOI:10.1007/s11538-013-9834-5 [本文引用: 2]
Healthcare-associated bacteraemia caused by Leuconostoc species at a university hospital in Taiwan between 1995 and 2008
DOI:10.1016/j.jhin.2010.11.014 [本文引用: 1]
主要海水养殖鱼类白点病和盾纤毛虫病防治技术
DOI:10.3969/j.issn.1003-1278.2007.06.037 [本文引用: 1]
Control of white - spot disease and scuticociliatida disease of some main cultured sea fishes
DOI:10.3969/j.issn.1003-1278.2007.06.037 [本文引用: 1]
A dynamic model of hepatitis B virus with delayed immune response
A reaction-diffusion malaria model with seasonality and incubation period
DOI:10.1007/s00285-017-1193-7 [本文引用: 1]
Spatial-temporal basic reproduction number and dynamics for a dengue disease diffusion model for a dengue disease diffusion model
DOI:10.1002/mma.5085 [本文引用: 1]
Threshold dynamics of reaction-diffusion partial differential equations model of Ebola virus disease
DOI:10.1142/S1793524518501085 [本文引用: 1]
Influence of temperature and host species on the development of cryptocaryon irritans
Complex dynamic behavior in a viral model with delayed immune response
DOI:10.1016/j.physd.2006.12.001
Analysis of a viral infection model with delayed immune response
DOI:10.1016/j.apm.2009.11.005 [本文引用: 1]
Hopf bifurcation induced by delay effect in a diffusive tumor-immune system
DOI:10.1142/S0218127418501365 [本文引用: 2]
Periodic solutions and chaos in a nonlinear model for the delayed cellular immune response
Turing instability and Turing-Hopf bifurcation in diffusive Schnakenberg systems with gene expression time delay
DOI:10.1007/s10884-018-9702-y [本文引用: 4]
Spatiotemporal complexity of a ratio-dependent predator-prey system
DOI:10.1103/PhysRevE.75.051913
Instabilities in spatially extended predator-prey systems: spatio-temporal patterns in the neighborhood of Turing-Hopf bifurcations
DOI:10.1016/j.jtbi.2006.09.036
Spatiotemporal dynamics of the diffusive Mussel-Algae model near Turing-Hopf bifurcation
Finite-difference schemes for reaction-diffusion equations modeling predator-prey interactions in MATLAB
DOI:10.1007/s11538-006-9062-3 [本文引用: 1]