1 引言
众所周知, 不同的休假规则和控制策略可以对系统的队长和顾客的等待时间产生重大影响. 如果服务员假期中到达的顾客数过多, 会形成拥挤现象, 这可能会降低服务质量和顾客的满意度. 此外, 在没有休假控制策略的排队系统中, 系统如果长时间频繁转换其状态, 则将会产生大量的转换成本. 因此, 为了有效地控制假期中的队长并克服系统频繁转换所带来的费用问题, 研究带有联合控制策略的排队系统是很有实际意义的. 到目前为止, 具有休假策略和多阀值控制策略的排队系统已得到了广泛的研究. 有关休假排队的研究可见参考文献[1-6]. 在早期的研究中, 大部分的工作都集中于讨论具有单重休假和多重休假的排队系统. 后来, 田乃硕在文献[4] 中首次引入了更一般的多级适应性休假策略. 田乃硕[4]研究了具有多级适应性休假的连续时间
在
在实际生活中, 服务员休假时间的长短不仅取决于在假期中所要从事的辅助工作量, 也会受到顾客到达过程的制约, 因此服务员的连续休假次数是不确定的. 鉴于此, 该文考虑具有多级适应性休假策略和Min(
2 模型描述
考虑一个具有多级适应性休假和Min(
(1) 顾客相继到达的间隔时间序列
(2) 第
(3) 系统中只有一个服务台且服务规则是先到先服务. 第
(4) 服务员采取多级适应性休假机制和系统采取Min(
其概率母函数为
(a) 在服务员休假期间开始一段新的服务员忙期(假期中有顾客到达, 且系统中的顾客数达到了
(b) 在服务员的某一次假期结束后, 开始一段新的服务员忙期(假期中有顾客到达, 但顾客数没有达到
(c) 在服务员闲期开始一段新的服务员忙期(服务员连续
(5) 随机变量
注2.1 (1) 服务员对每个顾客的工作量是指顾客需要完成的服务项目中所包含的事件数量. 工作量的计量单位可以是计数单位、重量单位等等. 例如, 某顾客需要某工厂加工100件产品, 则这个工厂的工作量就是这100件产品. 又如, 如果一辆卡车到达一个仓库装载2000千克的材料, 则这个装载人员的工作量就是这2000千克的材料.
(2) 在实际应用中, 改进以后的
(3) 当
3 系统稳态队长的随机分解
为方便后面的讨论, 我们先引入一些记号和定义.
定义3.1 服务员忙期: 从服务员开始为顾客服务的时刻起, 直到系统再次变空为止的这一段时间. 令
这里的
定义3.2 服务员非忙期: 从系统刚变空的时刻起, 直到服务员休假结束回到系统而且开始为顾客服务的时刻为止的这段时间.
定义3.3 系统周期: 从系统刚变空的时刻起, 直到其后第一个顾客到达的时刻为止的这一段时间. 显然地, 系统闲期是顾客的剩余到达间隔时间. 令
定义3.4 系统忙期: 从服务员忙期结束后第一个顾客到达空闲系统的时刻起, 直到系统再次变空为止的这段时间.
定理3.1 令
而且平均稳态队长
其中
证 当
(a) 在服务员休假期间开始一段新的服务员忙期(假期中有顾客到达, 且系统中的顾客数达到了
(b) 在服务员的某一次假期结束后, 开始一段新的服务员忙期(假期中有顾客到达, 但顾客数没有达到
(c) 在服务员闲期开始一段新的服务员忙期(服务员连续
同时, 根据工作量的含义可知, 服务员对等待顾客的累积工作量完全取决于顾客需要完成的服务项目中所包含的事件数量, 而不是取决于顾客的累积服务时间, 故服务员忙期的开始时刻是一个再生时刻点. 又由于随机变量
在文献[30] 中, 经典
在文献[3] 中, 附加队长分布的概率母函数为
其中,
基于多级适应性休假机制和Min(
因此, 服务员忙期开始时系统内的平均顾客数
当
其中,
将式(3.4), (3.5), (3.6) 和(3.7) 代入到式(3.3) 即可得式(3.1). 再由
可得式(3.2).
4 平均服务员忙期与服务员忙循环
本节分析几个重要的性能指标, 如平均服务员忙期、平均服务员非忙期以及忙循环.
(1) 平均服务员忙期
令
(2) 平均服务员非忙期
令
(3) 平均服务员忙循环
令
5 特殊情形
下面我们通过本文所获得的结果, 直接导出一些特殊排队模型的平均队长和平均忙循环.
推论5.1 当连续休假次数
平均忙循环为
其中
推论5.2 当
平均忙循环为
其中
推论5.3 当休假时间是定长
平均忙循环为
推论5.4 当休假时间是定长
平均忙循环为
推论5.5 当
平均忙循环为
这与文献[18] 的相应结果完全一致.
推论5.6 当
平均忙循环为
其中
推论5.7 当
平均忙循环为
其中
6 成本优化下的最优控制策略
为了证实前面所得的排队指标的实用性, 本节从经济利益的角度出发, 讨论系统的最优控制问题. 我们先建立了一个单位时间期望成本费用函数, 其中
使用上面定义的费用项目和前面所得到的相应的性能指标, 并结合更新报酬的知识, 可得到费用目标函数为
其中
例6.1 假设连续休假次数
表 1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 30.0000 | 25.8207 | 25.4800 | 25.4615 | 25.4614 | 25.4615 | 25.4615 |
| 5 | 30.0000 | 21.8145 | 20.5209 | 20.4796 | 20.6078 | 20.6890 | 20.7213 |
| 9 | 30.0000 | 21.2398 | 19.6983 | 19.7409 | 20.1381 | 20.5002 | 20.7321 |
| 12 | 30.0000 | 21.1440 | 19.5367 | 19.6127 | 20.1577 | 20.7372 | 21.1888 |
| 18 | 30.0000 | 21.1069 | 19.4623 | 19.5593 | 20.2405 | 21.0868 | 21.8986 |
| 23 | 30.0000 | 21.1037 | 19.4542 | 19.5541 | 20.2671 | 21.1978 | 22.1613 |
| 31 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2762 | 21.2409 | 22.2819 |
| 32 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2764 | 21.2424 | 22.2864 |
| 33 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2766 | 21.2434 | 22.2900 |
| 33.4013 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2767 | 21.2438 | 22.2912 |
| 33.4017 | 30.0000 | 21.1032 | 19.4527 | 19.5533 | 20.2767 | 21.2438 | 22.2912 |
| 33.4018 | 30.0000 | 21.1032 | 19.5533 | 20.2767 | 21.2438 | 22.2912 | |
| 33.41 | 30.0000 | 21.1032 | 19.4526 | 19.5533 | 20.2767 | 21.2438 | 22.2912 |
| 33.7 | 30.0000 | 21.1032 | 19.4526 | 19.5533 | 20.2767 | 21.2440 | 22.2920 |
| 38 | 30.0000 | 21.1032 | 19.4526 | 19.5533 | 20.2770 | 21.2459 | 22.2987 |
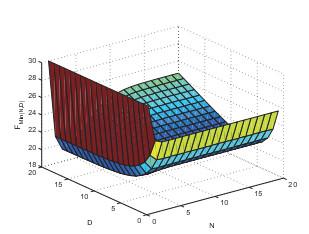
图 1
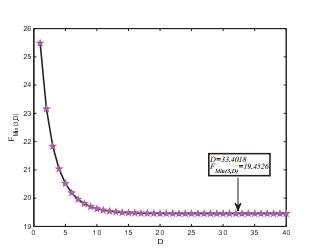
图 2
如果服务员最多连续休假为
其中
由式(6.3)可以看出,
例6.2 假设顾客的到达间隔时间
由于
当
表 2
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 26.2741 | 25.7841 | 25.7052 | 25.6922 | 25.6900 | 25.6896 | 25.6896 | 25.6896 |
| 5 | 22.4964 | 21.7610 | 21.6467 | 21.6279 | 21.6248 | 21.6243 | 21.6242 | 21.6242 |
| 9 | 21.9370 | 21.1854 | 21.0692 | 21.0501 | 21.0469 | 21.0464 | 21.0463 | 21.0463 |
| 13 | 21.8300 | 21.0759 | 20.9595 | 20.9403 | 20.9372 | 20.9366 | 20.9365 | 20.9365 |
| 18 | 21.8069 | 21.0523 | 20.9358 | 20.9166 | 20.9134 | 20.9129 | 20.9128 | 20.9128 |
| 23 | 21.8038 | 21.0491 | 20.9326 | 20.9134 | 20.9102 | 20.9097 | 20.9096 | 20.9096 |
| 28 | 21.8033 | 21.0487 | 20.9322 | 20.9130 | 20.9098 | 20.9093 | 20.9092 | 20.9092 |
| 29 | 21.8033 | 21.0486 | 20.9321 | 20.9130 | 20.9098 | 20.9092 | 20.9092 | 20.9091 |
| 29.2348 | 21.8033 | 21.0486 | 20.9321 | 20.9130 | 20.9098 | 20.9092 | 20.9092 | 20.9091 |
| 29.2349 | 21.8033 | 21.0486 | 20.9321 | 20.9130 | 20.9098 | 20.9092 | 20.9091 | |
| 29.235 | 21.8033 | 21.0486 | 20.9321 | 20.9130 | 20.9098 | 20.9092 | 20.9091 | 20.9091 |
| 31 | 21.8033 | 21.0486 | 20.9321 | 20.9129 | 20.9097 | 20.9092 | 20.9091 | 20.9091 |
| 32 | 21.8033 | 21.0486 | 20.9321 | 20.9129 | 20.9097 | 20.9092 | 20.9091 | 20.9091 |
表 3
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 25.9566 | 25.4416 | 25.3591 | 25.3455 | 25.3432 | 25.3428 | 25.3428 | 25.3427 |
| 5 | 21.1710 | 20.4708 | 20.3642 | 20.3467 | 20.3437 | 20.3433 | 20.3432 | 20.3432 |
| 9 | 20.3280 | 19.6502 | 19.5480 | 19.5312 | 19.5284 | 19.5280 | 19.5279 | 19.5279 |
| 13 | 20.1331 | 19.4640 | 19.3633 | 19.3468 | 19.3441 | 19.3436 | 19.3435 | 19.3435 |
| 18 | 20.0815 | 19.4151 | 19.3149 | 19.2985 | 19.2958 | 19.2953 | 19.2952 | 19.2952 |
| 23 | 20.0729 | 19.4070 | 19.3069 | 19.2905 | 19.2878 | 19.2873 | 19.2873 | 19.2872 |
| 28 | 20.0715 | 19.4057 | 19.3056 | 19.2892 | 19.2865 | 19.2860 | 19.2860 | 19.2860 |
| 33 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2858 | 19.2858 |
| 34 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2858 | 19.2857 |
| 34.53 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2858 | 19.2857 |
| 34.5301 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2857 | |
| 34.5302 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2857 | 19.2857 |
| 34.9 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2857 | 19.2857 |
| 35 | 20.0713 | 19.4055 | 19.3054 | 19.2890 | 19.2863 | 19.2858 | 19.2857 | 19.2857 |
表 4
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 25.9386 | 25.4231 | 25.3406 | 25.3269 | 25.3247 | 25.3243 | 25.3242 | 25.3242 |
| 5 | 21.0841 | 20.4333 | 20.3349 | 20.3187 | 20.3160 | 20.3156 | 20.3155 | 20.3155 |
| 9 | 20.2842 | 19.6997 | 19.6125 | 19.5983 | 19.5959 | 19.5955 | 19.5954 | 19.5954 |
| 13 | 20.1117 | 19.5548 | 19.4721 | 19.4585 | 19.4563 | 19.4559 | 19.4558 | 19.4558 |
| 18 | 20.0675 | 19.5210 | 19.4399 | 19.4266 | 19.4244 | 19.4241 | 19.4240 | 19.4240 |
| 23 | 20.0602 | 19.5160 | 19.4353 | 19.4221 | 19.4199 | 19.4196 | 19.4195 | 19.4195 |
| 27 | 20.0591 | 19.5154 | 19.4347 | 19.4215 | 19.4194 | 19.4190 | 19.4189 | 19.4189 |
| 28 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4189 | 19.4189 |
| 28.9233 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4189 | 19.4188 |
| 28.9234 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4189 | 19.4188 |
| 28.9235 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4188 | |
| 28.9236 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4188 | 19.4188 |
| 29 | 20.0590 | 19.5153 | 19.4347 | 19.4215 | 19.4193 | 19.4189 | 19.4188 | 19.4188 |
| 30 | 20.0589 | 19.5153 | 19.4346 | 19.4214 | 19.4193 | 19.4189 | 19.4188 | 19.4188 |
表 5
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 1 | 25.9384 | 25.4230 | 25.3405 | 25.3268 | 25.3246 | 25.3242 | 25.3241 | 25.3241 |
| 5 | 21.1883 | 20.5634 | 20.4691 | 20.4537 | 20.4511 | 20.4507 | 20.4506 | 20.4506 |
| 6 | 20.9145 | 20.3206 | 20.2315 | 20.2169 | 20.2144 | 20.2140 | 20.2140 | 20.2140 |
| 7 | 20.7558 | 20.1900 | 20.1055 | 20.0916 | 20.0893 | 20.0889 | 20.0889 | 20.0889 |
| 8 | 20.6677 | 20.1262 | 20.0456 | 20.0324 | 20.0302 | 20.0298 | 20.0298 | 20.0297 |
| 9 | 20.6229 | 20.1016 | 20.0242 | 20.0115 | 20.0094 | 20.0091 | 20.0090 | 20.0090 |
| 9.3939 | 20.6130 | 20.0987 | 20.0224 | 20.0099 | 20.0079 | 20.0075 | 20.0075 | 20.0074 |
| 9.3940 | 20.6130 | 20.0987 | 20.0224 | 20.0099 | 20.0079 | 20.0075 | 20.0074 | |
| 9.3941 | 20.6130 | 20.0987 | 20.0224 | 20.0099 | 20.0079 | 20.0075 | 20.0074 | 20.0074 |
| 9.3942 | 20.6130 | 20.0987 | 20.0224 | 20.0099 | 20.0079 | 20.0075 | 20.0074 | 20.0074 |
| 9.9 | 20.6050 | 20.0988 | 20.0238 | 20.0116 | 20.0095 | 20.0092 | 20.0091 | 20.0091 |
| 10 | 20.6039 | 20.0993 | 20.0245 | 20.0123 | 20.0102 | 20.0099 | 20.0098 | 20.0098 |
| 11 | 20.6001 | 20.1089 | 20.0362 | 20.0244 | 20.0224 | 20.0221 | 20.0220 | 20.0220 |
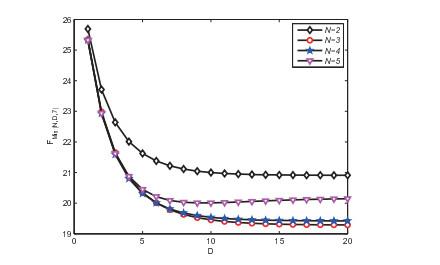
图 3
参考文献
Stochastic decompositions in the M/G/1 queue with generalized vacations
DOI:10.1287/opre.33.5.1117 [本文引用: 3]
Queueing systems with vacations: a survey
多级适应性休假的M/G/1 排队
M/G/1 queue with adaptive multistage vacations
Discrete time Geo/G/1 queue with multiple adaptive vacations
DOI:10.1023/A:1010947911863 [本文引用: 1]
多级适应性休假MX/G/1 排队系统的队长分布
DOI:10.3969/j.issn.1000-0577.2007.06.011 [本文引用: 1]
The queue length distribution of MX/G/1 queueing system with adaptive multistage vacations
DOI:10.3969/j.issn.1000-0577.2007.06.011 [本文引用: 1]
带有Bernoulli反馈的多级适应性休假的Geo/G/1 排队系统分析
Analysis of Geo/G/1 queueing system with multiple adaptive vacations and Bernoulli feedback
On the discrete-time Geo/G/1 queue with randomized vacations and at most J vacations
DOI:10.1016/j.apm.2010.11.021 [本文引用: 1]
On a discrete-time GIX/Geo/1/N−G queue with randomized working vacations and at most J vacations
A discrete-time Geo/G/1 retrial queue with J-vacation policy and general retrial times
The impact of the NT-policy on the behaviour of a discrete-time queue with general service times
基于单重休假的Min(N,V) -策略M/G/1 排队系统分析
Analysis of M/G/1 queueing system with Min(N,V)-policy based on single server vacation
基于多重休假的Min(N,V) -策略M/G/1 排队系统的队长分布
The queue length distribution of M/G/1 queueing system with Min(N,V) -policy based on multiple server vacations
Analysis of an M/G/1 queue with multiple vacations, N-policy, unreliable service station and repair facility failures
Design strategy for optimizing power consumption of sensor node with Min(N,T) policy M/G/1 queuing model
DOI:10.1002/dac.1288 [本文引用: 1]
The structure of departure process and optimal control policy N∗ for Geo/G/1 discrete-time queue with multiple server vacations and Min(N,V)-policy
具有多级适应性休假和Min(N,V) -策略控制的M/G/1 排队系统
M/G/1 queueing system with multiple adaptive vacations and Min(N,V)-policy
Control policy for a single server system
DOI:10.1287/mnsc.19.9.1013 [本文引用: 1]
On the D-policy for M/G/1 queue
On the M/G/1 queue with D-policy
DOI:10.1016/S0307-904X(01)00031-2 [本文引用: 1]
A note on the optimality of the N- and D-policies for the M/G/1 queue
DOI:10.1016/S0167-6377(02)00148-7
Queue length analysis of MAP/G/1 queue under D-policy
Analysis of MX/G/1 queue under D-policy
A mean value formula for the M/G/1 queues controlled by workload
DOI:10.1016/j.orl.2006.08.001 [本文引用: 1]
The performance of the M/G/1 queue under the dyadic Min(N,D)-policy and its cost optimization
DOI:10.1016/j.peva.2008.04.006 [本文引用: 1]
Analysis of the MAP/G/1 queue under the Min(N,D)-policy
DOI:10.1080/15326340903517121 [本文引用: 1]
基于Min(N,D,V) -策略和单重休假的M/G/1 排队系统的最优控制策略
Analysis and optimal policy for M/G/1 queueing system under Min(N,D,V)-policy control
Queueing Processes in bulk systems under D-policy