1 引言
称两个度量空间
我们称
我们称
我们称
我们称吸引子
Lipschitz等价问题的研究主要有两种类型. 第一类由Falconer和Marsh[2]提出: 假设两个自相似集满足SSC, 那么它们的压缩比满足什么条件时, 它们是Lipschitz等价的, 这类问题主要的研究方法是构造Lipschitz不变量(参见文献[6-9]); 第二类由David和Semmes[4]提出: 假设两个自相似集有相同的压缩比, 那么它们分支的几何结构是如何影响Lipschitz等价性的, 这类问题主要的研究方法是直接构造它们之间的双Lipschitz映射. 由于这类问题的研究非常困难, 目前只有较少的结果, 参见文献[10-18], 而这类问题的第一个实质性进展是饶辉, 阮火军和奚李峰[10]取得的, 即{1, 3, 5}-{1, 4, 5} 问题.
定理 1.1 设
图 1
本文的结构如下: 第2节, 我们介绍了符号空间, 分离数, 急速分离条件和邻居自动机等概念, 它们在证明映射是Lipschitz等价的过程中起到了重要的作用; 第3节, 我们引入了词分解等概念, 利用词分解来构造符号空间上的双射
2 邻居自动机
在本节中, 我们将引入分离数和邻居自动机等概念.
2.1 符号空间和投影映射
设
设
定义映射
称
2.2 分离数
下面进一步假设
其中
定义 2.1 设
如果
通过分离数, 我们可以在
定义 2.2 设
其中dist
引理 2.1 设自相似集
是双Lipschitz映射. 即, 存在一个常数
2.3 邻居自动机
为了计算分离数, 我们引入邻居自动机. 设
现在, 我们构造
其中
其次, 设
即: 如果
设
其中,
由上述定义, 下面的引理显然成立.
引理 2.2 设
2.4 邻居自动机
E -自动机和F -自动机
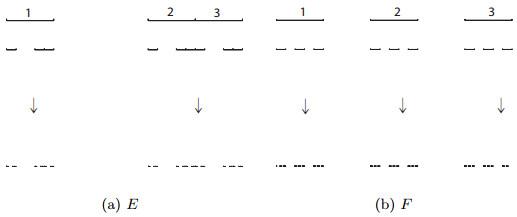
定理1.1中的自相似集
对于集合
那么,
邻居映射集和
其中
图 2
F -自动机如图 2(b)所示.
3 构造双Lipschitz映射
在本节中, 我们将通过翻译机构造一个符号空间之间的双射.
3.1 有效词分解
现在, 我们介绍
定义 3.1 (
由定义3.1容易证明, 一个词的任何字母是不可能同时属于两个不同的特殊词, 这点是词的分解唯一性的保证.
定义 3.2 设
其中
例 3.1 词
定义 3.3 (
3.2 符号空间之间的映射g
接下来, 我们定义映射
那么
定义映射
其中
例3.1中的词在映射
引理 3.1 如果
证 令
首先, 证明
其次, 证明
定理 3.1
证 首先, 由引理3.1可知,
3.3 翻译机
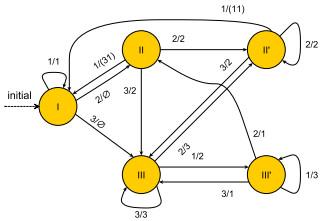
映射
图 3
其中状态
引理 3.2 设
证 根据图 3, 观察到, 除了离开状态
3.4 构造双Lipschitz映射
定义映射
由引理2.1, 映射
定理 3.2 映射
4 定理3.2的证明
在这一节中, 我们将证明定理4.1, 并且根据它我们可以直接得到定理3.2.
定理 4.1 设
在这一节中, 不失一般性, 我们总记
我们将经常用到下述简单事实: 对于任意的
由分离数的定义可知,
下面引理给出了
引理 4.1 设
证 由引理的条件可知,
若
若
假设
(i) 当
这是因为, 当
(ii) 当
这是因为, 当
证毕.
显然, 为了证明定理4.1, 我们仅须证明该定理在
引理 4.2 如果
证
引理得证.
引理 4.3 如果
证
Case 1.
此时,
故(4.1)式成立.
Case 2.
此时,
若
因此, 由引理4.1可知, (4.1)式成立.
Case 3.
此时,
因此, 由引理4.1可知, (4.1)式成立. 下面我们考虑
若
如果
因此, 由引理4.1可知, (4.1)式成立.
如果
所以
另一方面, 由
从而
因此由引理4.1可知, (4.1)式成立. 引理得证.
引理 4.4 如果
证 由对称性, 不妨设
所以
如果
所以
显然, 当
下面, 我们需要证明
(i) 若
(ii) 若
此时, 由
这与假设
综上, 我们有
因此, (4.1)式成立.
定理3.2的证明 由定理4.1可知, 映射
参考文献
On the shape of Cantor sets
On the Lipschitz equivalence of Cantor sets
DOI:10.1112/S0025579300014959 [本文引用: 2]
Classification of quasi-circles by Huasdorff dimension
Lipschitz equivalence of Cantor sets and algebraic properties of contraction ratios
DOI:10.1090/S0002-9947-2011-05327-4 [本文引用: 1]
Higher dimensional Frobenius problem: Maximal saturated cone, growth function and rigidity
DOI:10.1016/j.matpur.2015.03.007
Higher dimensional Frobenius problem and Lipschitz equivalence of Cantor sets
DOI:10.1016/j.matpur.2015.05.006 [本文引用: 1]
Lipschitz equivalence of self-similar sets
DOI:10.1016/j.crma.2005.12.016 [本文引用: 5]
Self-similar sets with initial cubic patterns
DOI:10.1016/j.crma.2009.12.006
Lipschitz equivalence of fractals generated by nested cubes
Lipschitz equivalence of self-similar sets with touching structures
DOI:10.1088/0951-7715/27/6/1299
Topological invariants and Lipschitz equivalence of fractal squares
DOI:10.1016/j.jmaa.2017.02.012
一对分形方块的利普希茨等价
Lipschitz equivalence of a pair fractal squares
Lipschitz equivalence of self-similar sets with two-state automation
DOI:10.1016/j.jmaa.2017.09.007 [本文引用: 2]