1 引言
近年来, 越来越多的研究关注自催化模型的动力学行为, 通过对反应扩散系统的定性分析和数值模拟, 更清楚地展示反应物的振荡现象, 对化学过程的认知产生重要意义.文献[1]研究了一类自催化三分子生化反应扩散模型, 建立了正平衡点的稳定性和非常数稳态解的存在性.本文考虑具有可逆效应的自催化三分子生化反应扩散模型, 其化学反应机制为
其中
其中
在系统(1.1)不考虑可逆反应的情况下, 文献[3]研究了施加电场对反应动力学的影响, 并利用线性稳定性分析和数值模拟说明了电场对空间结构的影响.文献[4]讨论了唯一正平衡点的稳定性, 并利用Lyapunov-Schmidt技术和奇异理论, 研究了空间非均匀平稳结构, 特别是双特征值分支结构.生化反应过程是一个复杂的过程, 受到许多复杂机制的影响, 常常伴随着多重平衡态、时间震荡行为和稳定性发生改变的分支现象. Hopf分支理论作为研究非线性方程的经典工具, 被广泛应用.文献[5]研究了任意阶自催化模型Hopf分支的存在性和稳定性.文献[6]研究了具有自催化和饱和规律的双分子反应扩散模型, 考虑了由惟一正平衡点产生的Hopf分支和稳态分支.更多关于Hopf分支的研究有兴趣的读者可参见文献[7-10]及其中的参考文献.
本文主要研究系统(1.1)Hopf分支的存在性、稳定性及由扩散引起的Turing不稳定性.
2 常微分系统的Hopf分支及稳定性
易知, 系统(1.1)所对应的常微分系统
存在惟一的正平衡点
设其特征方程为
设
定理2.1 设
(ⅰ) 若
(ⅱ) 若
(ⅲ) 若
证 (ⅰ) 当
(ⅱ) 当
(ⅲ) 当
经计算
令
将上述系统泰勒展开为
其中
定义
其中
作变换
代入系统(2.2)得
其中
由文献[5]知, 分支的方向以及分支周期解的稳定性由
由
进一步计算得
将上述等式代入
由Poincare-Andronov-Hopf分支定理[11]可知, 系统(2.1)在正平衡点
3 扩散系统的Turing不稳定性和Hopf分支
本节在一维空间
的Hopf分支.
定义实Sobolev空间
并且定义
系统(3.1)在
在齐次Neumann边界条件下, 算子
且
令
为
其中
其中
显然, 当
下面考虑系统(3.1)当
当
注意到二次函数
的判别式为
因此
如果
定理3.1 设
(ⅰ) 当
(ⅱ) 当
下面讨论
存在两个正实根
其中
当
令
则
由于
定义
要使不等式
固定
从而对所有的
如果
定理3.2 设
则对于固定的
固定
因此, 存在
定理3.3 设
定理3.4 令
如果
证 如果
由前面的计算可知, 当
由文献[12]知, 分支的方向和分支周期解的稳定性由
由文献[12]的定理2.1可知, 如果
那么分支是超临界的(或次临界的).另外, 若
设
其中
令
满足
定义
其中
当
其中
按照内积定义计算可得
令
其中
计算得
进一步计算得
由文献[13]中的Hopf分支定理知, 系统(3.1)在
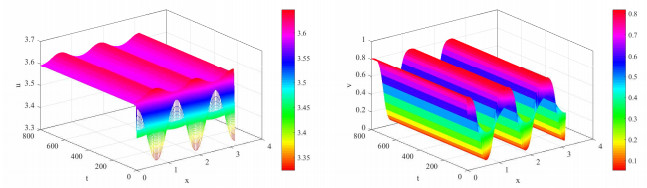
4 数值模拟
本节利用Matlab软件给出具体的数值实例, 以验证补充前面给出的结果.
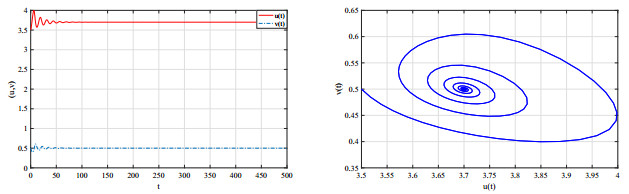
图 1
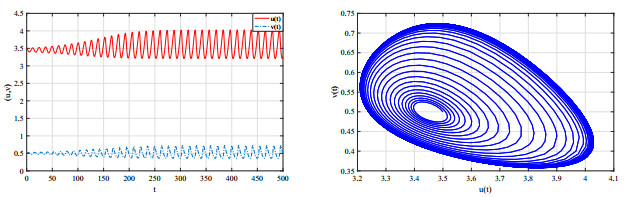
图 2
扩散系统(3.1)包含五个参数:
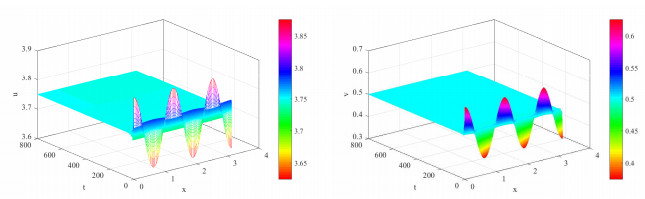
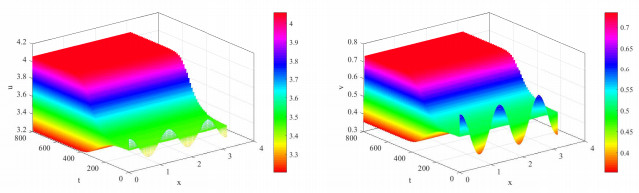
图 3
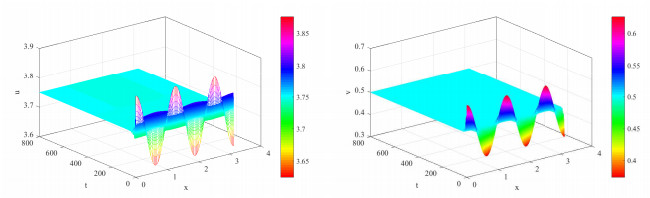
图 4
图 5
图 6
图 6
参数
左:
5 小结
本文在Neumann边界条件下研究一类自催化可逆三分子生化反应模型, 以可逆反应率为参数, 分别给出常微分系统和扩散系统的Hopf分支及其稳定性.特别对扩散系统, 给出扩散系数对系统稳定性的影响.结果表明, 当可逆反应率较小时, 正平衡点不稳定; 当可逆反应率较大时, 正平衡点稳定; 当可逆反应率介于某一范围内时, 扩散系数会对系统的稳定性产生较大影响.此时, 当催化剂的扩散系数较小时, 会产生Turing不稳定性.
参考文献
Qualitative analysis on positive steady-states for an autocatalytic reaction model in thermodynamics
DOI:10.3934/dcds.2017206 [本文引用: 1]
Depressing the bistable behavior of the iodate-arsenous acid reaction in a continuous flow stirred tank reactor by the effect of chloride or bromide ions: A method for determination of rate constants
DOI:10.1021/j100281a048 [本文引用: 1]
Creation of spatial structure by an electric field applied to an ionic cubic autocatalator system
DOI:10.1023/A:1004799200173 [本文引用: 1]
Steady-state solutions and stability for a cubic autocatalysis model
DOI:10.3934/cpaa.2015.14.1147 [本文引用: 1]
Hopf bifurcation in spatially homogeneous and inhomogeneous autocatalysis models
DOI:10.1016/j.camwa.2013.08.014 [本文引用: 2]
Spatiotemporal pattern formation of a diffusive bimolecular model with autocatalysis and saturation law
DOI:10.1016/j.camwa.2013.08.022 [本文引用: 1]
Hopf bifurcation in a reaction-diffusion equation with distributed delay and Dirichlet boundary condition
DOI:10.1016/j.jde.2017.07.024 [本文引用: 1]
密度制约且具有时滞捕食-被捕食模型的Hopf分支
DOI:10.3969/j.issn.1003-3998.2019.02.015
Hopf bifurcation of delayed density-dependent predator-prey model
DOI:10.3969/j.issn.1003-3998.2019.02.015
Spatiotemporal pattern formation and multiple bifurcations in a diffusive bimolecular model
DOI:10.1016/j.nonrwa.2010.02.007
一类具有自动催化作用和饱和定律的双分子模型的图灵不稳定性和霍普夫分歧
DOI:10.3969/j.issn.1003-3998.2017.02.015 [本文引用: 1]
Turing instability and Hopf bifurcation of a bimolecular model with autocatalysis and saturation law
DOI:10.3969/j.issn.1003-3998.2017.02.015 [本文引用: 1]
Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator-prey system