在非线性数学物理领域,特别是可积系统中,如何寻找具有Lax对的新的非线性演化方程,并研究这些可积方程的显式解,一直以来都是一项重要的研究课题.寻找显式解和守恒律为考察孤子方程的很多性质都提供了重要的途径.众所周知,有许多求解可积方程的显式解的有效方法,比如:反散射变换^[1-2]、Hirota方法^[3]、Backlund变换和Darboux变换^[4-8]、代数几何方法^[9-11],等等^[12-16].在这些方法中, Darboux变换方法是非常有效的^[17-21].

用来描述水波沿两个方向运动的Boussinesq方程出现在很多物理系统里,也有很多的变形方程^[22-23].该文的目的就是提出一个与$ 3\times3 $矩阵谱问题相联系的形变Boussinesq型非线性演化微分方程族,方程族中前两个非平凡的方程为

(1.1) $ \begin{equation} \begin{array}{lcl} u_{t} = 3u_{xx}-u_{x}-6v_{x}, \\ v_{t} = 2u_{xxx}-2uu_{x}-3v_{xx}-2u_{xx}+3v_{x}, \end{array} \end{equation} $

(1.2) $ \begin{equation} \begin{array}{lcl} u_{t} = (18v_{xx}-9u_{xxx}+6u_{xx}+18uu_{x}+3u_{x}-36uv-6v-12u^2-4u)_x, \\ v_{t} = (9v_{xxx}-6u_{xxxx}+6u_{xxx}-6v_{xx}+18uu_{xx}+9u_{x}^2+2u_{xx}-18uv_{x}-3v_{x}\\ \quad\quad-12uu_{x}-2u_{x}-18v^2-4u^3-u^2)_x. \end{array} \end{equation} $

然后我们得到了这两个非平凡方程的无穷多守恒律.最后,通过考虑相应的$ 3\times 3 $矩阵谱问题之间的规范变换,得到了方程(1.1)的Darboux变换和一些显式解.

为了得到形变Boussinesq型方程族,我们首先引入一个如下的$ 3\times 3 $矩阵谱问题

(2.1) $ \begin{equation} \psi_x = U\psi, \quad \psi = \left(\begin{array}{ccc}\psi_1\\ \psi_2\\ \psi_3\end{array}\right), \quad U = \left(\begin{array}{ccc}0&{\quad} u{\quad}&\lambda+v\\ 1&1&0\\ 0&1&0\end{array}\right), \end{equation} $

其中$ u, v $是两个位势, $ \lambda $是一个常值谱参数.我们先求解驻定的零曲率方程

(2.2) $ \begin{equation} V_x-[U, V] = 0, \quad V = \left(\begin{array}{ccc}V_{11}&V_{12}&V_{13}\\ V_{21}&{\quad} V_{22}{\quad}&V_{23}\\ V_{31}&V_{32}&V_{33}\end{array}\right). \end{equation} $

该方程等价于

(2.3) $ \begin{equation} \begin{array}{lll} &V_{11, x}+V_{12}-uV_{21}-(\lambda+v)V_{31} = 0, \\ &V_{12, x}+V_{12}+V_{13}+u(V_{11}- V_{22})-(\lambda+v)V_{32} = 0, \\ &V_{13, x}-uV_{23}+(\lambda+v)(V_{11}- V_{33}) = 0, \\ &V_{21, x}-V_{21}+V_{22}-V_{11} = 0, \\ &V_{22, x}+V_{23}-V_{12}+uV_{21} = 0, \\ &V_{23, x}-V_{13}-V_{23}+(\lambda+v)V_{21} = 0, \\ &V_{31, x}+V_{32}-V_{21} = 0, \\ &V_{32, x}+V_{33}-V_{22}+uV_{31}+V_{32} = 0, \\ &V_{33, x}-V_{23}+(\lambda+v)V_{31} = 0. \end{array} \end{equation} $

如果令$ (A, B) = \sum\limits_{j = 0}^{\infty}(A_j, B_j)\lambda^{-j} $,有

(2.4) $ \begin{equation} \begin{array}{rl} V_{11} = &{ } \frac{1}{3}(3\partial-1)A-\frac{1}{3}(\partial^2+\partial-u)B, \\ V_{12} = &{ } \frac{1}{3}(\partial-3\partial^2+3u)A+\frac{1}{3}(\partial^3+\partial^2-\partial u+3v)B+\lambda B, \\ V_{13} = &{ } \frac{1}{3}(2\partial^2-3\partial^3+\partial+3v)A+\frac{1}{3}(2\partial^4-2\partial^2u-2\partial^2+2\partial u+3\partial v-3v)B\\ &+\lambda[A+(\partial-1)B], \\ V_{21} = &A, \quad V_{22} = { } \frac{2}{3}A-\frac{1}{3}(\partial^2+\partial-u)B, \\ V_{23} = &{ } \frac{1}{3}(2\partial^3+2\partial^2-2\partial u+3v)B-\frac{1}{3}(3\partial^2+\partial)A+\lambda B, \\ V_{31} = &{ } B, \quad V_{32} = A-\partial B, \quad V_{33} = \frac{1}{3}(2\partial^2+2\partial-2u)B-\frac{1}{3}(3\partial+1)A, \end{array} \end{equation} $

然后把(2.4)式代入(2.3)式可得

(2.5) $ \begin{equation} K S_j = J S_{j+1}, \quad j\geq 0, \quad JS_0 = 0, \end{equation} $

其中$ S_j = (A_j, B_j)^T $,两个斜称算子分别为$ (\partial\partial^{-1} = \partial^{-1}\partial = 1) $

(2.6) $ \begin{equation} K = \left(\begin{array}{ccc} { } -2\partial^3+\partial u+u\partial+\frac{2}{3}\partial & \begin{array}{c}{ } \partial^4 +\frac{2}{3}\partial^3-\partial^2 u -\frac{1}{3}\partial^2\\ { }+2\partial v+v\partial+\frac{1}{3}\partial u\end{array} \\ { } -\partial^4+\frac{2}{3}\partial^3+u\partial^2+\frac{1}{3}\partial^2+\partial v+2v\partial+\frac{1}{3}u\partial&K_{22} \end{array}\right), \end{equation} $

(2.7) $ \begin{equation} J = \left(\begin{array}{ccc} 0&{\quad} -3\partial\\ -3\partial&{\quad} 2\partial\\ \end{array}\right), \end{equation} $

其中

$ \begin{eqnarray*} K_{22} = \frac{2}{3}\partial^5-\frac{2}{3}\partial^3u-\frac{2}{3}u\partial^3+\frac{2}{3}u\partial u+\partial^2 v-v\partial^2+\frac{2}{3}\partial^2 u-\frac{2}{3}u\partial^2-\frac{2}{3}\partial^3-\partial v-v\partial. \end{eqnarray*} $

为了方便地求解$ S_j $,我们定义两组Lenard递归方程

(2.8) $ \begin{equation} \begin{array}{lcr} K s_j = J s_{j+1}, \quad j\geq 0, \quad s_j\mid_{(u, v) = 0} = 0, \quad j\geq 1, \\ K \hat{s}_j = J \hat{s}_{j+1}, \quad j\geq 0, \quad \hat{s}_j\mid_{(u, v) = 0} = 0, \quad j\geq1, \end{array} \end{equation} $

此处的初值为$ s_0 = (1, 0)^T $, $ \hat{s}_0 = (0, 1)^T $.从而,我们可以唯一的得到$ s_j $和$ \hat{s}_j $,例如

(2.9) $ \begin{equation} s_1 = \left(\begin{array}{ccc} { } -\frac{1}{9}(2u+3v)\\ { } -\frac{1}{3}u \end{array}\right), \quad \hat{s}_1 = \left(\begin{array}{ccc}{ } \frac{1}{27}(6u_{xx}-3u^2-2u-9v_{x}-3v)\\ { } \frac{1}{9}(3u_{x}-u-6v)\end{array}\right), \end{equation} $

(2.10) $ \begin{equation} s_2 = \left(\begin{array}{ccc}s_2^{(1)}\\ s_2^{(2)} \end{array}\right), \quad\quad \hat{s}_2 = \left(\begin{array}{ccc}\hat{s}_2^{(1)}\\ \hat{s}_2^{(2)}\end{array}\right), \end{equation} $

其中

$ \begin{eqnarray*} s_2^{(1)}& = &\frac{1}{243}(27v_{xxx}-18u_{xxxx}+18v_{xx}+54uu_{xx}+18u_{xx}-54uv_{x}-9v_{x}+27u_{x}^2\\ &&-54v^2-72uv -12v-12u^3-27u^2-8u), \\ s_2^{(2)}& = &\frac{1}{81}(9u_{xxx}-18v_{xx}-6u_{xx}-18uu_{x}-3u_{x}+36uv+12u^2+4u+6v), \\ \hat{s}_2^{(1)}& = &\frac{1}{729}(27v_{xx}-27v_{xxxx}-27v_{xxx}+135uv_{xx}+270u_{xx}v+126u_{xx}u-405vv_{x}\\ &&+270u_{x}v_{x} +24u_{xx}-81uv_{x}-9v_{x}+63u_{x}^2-81v^2-135u^2v-108uv\\ &&-12v-48u^3-39u^2-8u), \\ \hat{s}_2^{(2)}& = &\frac{1}{243}(9u_{xxxx}-9u_{xxx}+18v_{xx}-45uu_{xx}-9u_{xx}-135u_{x}v-27uu_{x}\\ &&-3u_{x}+135v^2+54uv+6v+15u^3+18u^2+4u). \end{eqnarray*} $

易见方程$ JS_0 = 0 $具有通解

(2.11) $ \begin{equation} S_0 = \alpha_0s_0+\hat{\alpha}_0\hat{s}_0, \end{equation} $

从而函数$ S_j $可以表示为

(2.12) $ \begin{equation} S_j = \alpha_0s_j+\hat{\alpha}_0\hat{s}_j, \end{equation} $

该函数满足递归方程(2.5),且$ \alpha_0 $和$ \hat{\alpha}_0 $为任意常数.

假设$ \psi $满足谱问题(2.1)和辅谱问题

(2.13) $ \begin{equation} \psi_{t_n} = {V}^{(n)}\psi, \quad {V}^{(n)} = \left(\begin{array}{ccc} V^{(n)}_{11}&{\quad} V^{(n)}_{12}{\quad} & V^{(n)}_{13}\\ V^{(n)}_{21}& V^{(n)}_{22}& V^{(n)}_{23}\\ V^{(n)}_{31}& V^{(n)}_{32}& V^{(n)}_{33}\end{array}\right), \end{equation} $

其中$ {V}_{ij}^{(n)} = V_{ij} (A^{(n)}, B^{(n)}), (A^{(n)}, B^{(n)}) = \sum\limits_{l = 0}^{n}(A_l, B_l)\lambda^{n-l} $.方程(2.1)和(2.13)的相容性条件为零曲率方程$ U_{t_n}-{V}_x^{(n)}+[U, {V}^{(n)}] = 0 $,该方程等价于如下的非线性演化方程族

(2.14) $ \begin{equation} (u_{t_n}, v_{t_n})^T = K S_n = J S_{n+1}, \qquad n\geq0. \end{equation} $

方程族(2.14)中前两个非平凡的方程为

(2.15) $ \begin{eqnarray} u_{t_0}& = &\alpha_0u_{x}-\frac{1}{3}\hat{\alpha}_0(3u_{xx}-u_{x}-6v_{x}), {}\\ v_{t_0}& = &\alpha_0v_{x}-\frac{1}{3}\hat{\alpha}_0(2u_{xxx}-2uu_{x}-3v_{xx}-2u_{xx}+3v_{x}), {}\\ u_{t_1}& = &\frac{1}{27}\alpha_0(18v_{xxx}-9u_{xxxx}+6u_{xxx}+18uu_{xx}+3u_{xx} -36uv_{x}-6v_{x}+18u_{x}^2{}\\ &&-36u_{x}v-24uu_{x}-4u_{x})+\frac{1}{81}\hat{\alpha}_0(9u_{xxxx}-9u_{xxxxx}-18v_{xxx}+45uu_{xxx} {}\\ &&+9u_{xxx}+45u_{x}u_{xx}+135u_{xx}v+27uu_{xx}+3u_{xx} +135u_{x}v_{x}-270vv_{x}{}\\ &&-54uv_{x}-6v_{x}+27u_{x}^2-54u_{x}v-45u^2u_{x}-36uu_{x}-4u_{x}), \end{eqnarray} $

(2.16) $ \begin{eqnarray} v_{t_1}& = &\frac{1}{27}\alpha_0(9v_{xxxx}-6u_{xxxxx}+6u_{xxxx}-6v_{xxx} +18uu_{xxx}+2u_{xxx}-18uv_{xx}{}\\ &&-12uu_{xx}-3v_{xx}-2u_{xx}+36u_{x}u_{xx}-18u_{x}v_{x}-36vv_{x}-12u_{x}^2-12u^2u_{x}-2uu_{x}) {}\\ && +\frac{1}{81}\hat{\alpha}_0(6u_{xxxxx}-9v_{xxxxx}+45uv_{xxx} -9v_{xxxx}-6u_{xxxx}+90u_{xxx}v+12uu_{xxx}{}\\ &&+2u_{xxx}+21v_{xxx}+135u_{x}v_{xx}-135vv_{xx}-27uv_{xx} -3v_{xx}+180u_{xx}v_{x}{}\\ &&+54u_{x}u_{xx}-90u_{xx}v-18uu_{xx} -2u_{xx}-135v_{x}^2-45u^2v_{x}-18u_{x}^2-2uu_{x} {}\\ &&-117u_{x}v_{x}+126vv_{x}-90uu_{x}v-18u^2u_{x}). \end{eqnarray} $

如果选取$ \alpha_0 = 0, \hat{\alpha}_0 = -3, t_0 = t $,则方程(2.15)就约化为方程(1.1),如果令$ \alpha_0 = 27, $$ \hat{\alpha}_0 = 0, $$ t_1 = t $,则方程(2.16)可以约化为方程(1.2).

接下来,我们将考虑方程(2.15)和(2.16)的无穷多守恒律.令$ \phi = \frac{\psi_{3, x}}{\psi_3} $,从谱问题(2.1)可得如下的Riccati方程

(2.17) $ \begin{equation} \phi_{xx}+3\phi\phi_x+\phi^3-\phi^2-\phi_x-u\phi = \lambda+v. \end{equation} $

另一方面,从辅谱问题(2.13)可知

(2.18) $ \begin{equation} \frac{\psi_{3, t}}{\psi_3} = V_{31}^{(n)}(\phi^2+\phi_x-\phi)+V_{32}^{(n)}\phi+V_{33}^{(n)}. \end{equation} $

令

$ \theta = V_{31}^{(n)}(\phi^2+\phi_x-\phi)+V_{32}^{(n)}\phi+V_{33}^{(n)}, $

由于

$ \frac{\partial}{\partial_t}\frac{\psi_{3, x}}{\psi_3} = \frac{\partial}{\partial_x}\frac{\psi_{3, t}}{\psi_3}, $

从而

(2.19) $ \begin{equation} \phi_t = \theta_x. \end{equation} $

假设$ \lambda = \eta^3 $.把下面的假设

(2.20) $ \begin{equation} \phi = \sum\limits_{j = -1}^{\infty}\phi_j\eta^{-j} \end{equation} $

代入(2.17)式,并比较$ \lambda $的同次幂系数,可以得到$ \phi_j $的如下表达式

(2.21) $ \begin{eqnarray} &&\phi_{-1} = 1, \quad\phi_0 = \frac{1}{3}, \quad \phi_1 = \frac{1}{3}u+\frac{1}{9}, {}\\ &&\phi_2 = -\frac{1}{3}u_x+\frac{1}{9}u+\frac{1}{3}v+\frac{2}{81}, \quad \phi_3 = \frac{2}{9}u_{xx}-\frac{1}{9}u_{x}-\frac{1}{3}v_x, {}\\ &&\phi_j = \frac{1}{3}\bigg( {\sum\limits_{l = -1}^{j-1}\phi_l\phi_{j-2-l}}- {\sum\limits_{{l+m+n = j-2\atop -1\leq l, m, n<j}}\phi_l\phi_m\phi_n}-3 {\sum\limits_{l = -1}^{j-1}\phi_l\phi_{j-2-l, x}}\\ &&{\qquad}{\quad} +\phi_{j-2, x}-\phi_{j-2, xx}+u\phi_{j-2}\bigg), \quad j\geq3.{} \end{eqnarray} $

对于方程(2.15),我们选取$ n = 0 $,从而

(2.22) $ \begin{equation} V_{31}^{(0)} = \hat{\alpha}_0, \quad V_{32}^{(0)} = \alpha_0, \quad V_{33}^{(0)} = -\frac{1}{3}\alpha_0-\frac{2}{3}u\hat{\alpha}_0, \end{equation} $

同时把$ \theta $展开成如下关于$ \lambda $的级数

(2.23) $ \begin{equation} \theta = \hat{\alpha}_0\eta^2+\frac{1}{3}(3\alpha_0-\hat{\alpha}_0)\eta+ \sum\limits_{j = 1}^{\infty}\theta_j\eta^{-j}. \end{equation} $

接着,从(2.19)式即可得到$ \theta_j $的表示式

(2.24) $ \begin{eqnarray} &&\theta_1 = \alpha_0(\frac{1}{3}u+\frac{1}{9})+\hat{\alpha}_0(\frac{1}{9}u-\frac{1}{3}u_{x}+\frac{2}{3}v+\frac{1}{81}), {}\\ &&\theta_j = \hat{\alpha}_0\bigg(\sum\limits_{l = -1}^{j+1}\phi_l\phi_{j-l}+\phi_{j, x}-\phi_j\bigg)+\alpha_0\phi_j, \quad j\geq1. \end{eqnarray} $

$ \phi $和$ \theta $的展开式中的系数$ \phi_j $和$ \theta_j $分别被称为守恒密度和守恒流.方程(2.15)的第一个守恒律为

(2.25) $ \begin{equation} (\frac{1}{3}u+\frac{1}{9})_{t_0} = \alpha_0(\frac{1}{3}u+\frac{1}{9})_x+\hat{\alpha}_0(\frac{1}{9}u-\frac{1}{3}u_{x}+\frac{2}{3}v+\frac{1}{81})_x. \end{equation} $

对于方程(2.16),我们选取$ n = 1 $,从而

(2.26) $ \begin{eqnarray} V_{31}^{(1)}& = &{ } \frac{1}{9}\hat{\alpha}_0(3u_{x}-u-6v)-\frac{1}{3}\alpha_0u+\hat{\alpha}_0\lambda, {}\\ V_{32}^{(1)}& = &{ } \frac{1}{9}\alpha_0(3u_{x}-2u-3v)+\alpha_0\lambda+\frac{1}{27}\hat{\alpha}_0(3u_{x}-3u_{xx}-3u^2-2u+9v_{x}-3v), {}\\ V_{33}^{(1)}& = &{ } \frac{1}{81}\hat{\alpha}_0(6u_{xx}-9v_{xx}-18v_{x}+9u^2+2u+3v+36uv)-\frac{1}{3}(\alpha_0+2u\hat{\alpha}_0)\lambda{}\\ &&{ } -\frac{1}{27}\alpha_0(6u_{xx}-6u^2-9v_{x}-2u-3v). \end{eqnarray} $

借助于$ \theta $关于$ \lambda $的如下级数

(2.27) $ \begin{equation} \theta = \hat{\alpha}_0\eta^5+\frac{1}{3}(3\alpha_0-\hat{\alpha}_0)\eta^4+\frac{1}{81}(9\alpha_0+\hat{\alpha}_0)\eta^2 +\frac{1}{243}(6\alpha_0+\hat{\alpha}_0)\eta+ \sum\limits_{j = 1}^{\infty}\theta_j\eta^{-j}, \end{equation} $

我们可以从(2.19)式立即得到$ \theta_j $的表达式

(2.28) $ \begin{eqnarray} \theta_1& = &\frac{1}{81}\alpha_0(6u_{xx}-9u_{xxx}+18v_{xx}+18uu_{x}+3u_{x}-12u^2-36uv-4u-6v-\frac{2}{9}){}\\ &&+\frac{1}{243}\hat{\alpha}_0(9u_{xxx}-9u_{xxxx}+27uu_{x} +135u_{x}v+3u_{x}+9u_{xx}-18v_{xx}{}\\ &&-54uv+45uu_{xx}-4u-15u^3-18u^2-6v-135v^2-\frac{4}{27}), {}\\ \theta_j& = &(\alpha_0-\hat{\alpha}_0)\phi_{j+3}+\bigg[\frac{1}{9}\alpha_0(u-3v+3u_{x}){}\\ &&-\frac{1}{27}\hat{\alpha}_0(3u_{xx}+3u^2-u+6u_{x}-9v_{x}-15v)\bigg]\phi_{j} +\hat{\alpha}_0 \bigg( \sum\limits_{l = -1}^{j+4}\phi_l\phi_{j+3-l}+\phi_{j+3, x}\bigg){}\\ &&+\frac{1}{9}[\hat{\alpha}_0(3u_{x}-u-6v)-3\alpha_0u] \bigg( \sum\limits_{l = -1}^{j+1}\phi_l\phi_{j-l}+\phi_{j, x}\bigg), \quad j\geq1. \end{eqnarray} $

方程(2.16)的第一个守恒律为

(2.29) $ \begin{eqnarray} (\frac{1}{3}u+\frac{1}{9})_{t_1}& = &\frac{1}{81}\alpha_0(6u_{xx}-9u_{xxx}+18v_{xx}+18uu_{x} +3u_{x}-12u^2-36uv-4u-6v-\frac{2}{9})_x{}\\ && +\frac{1}{243}\hat{\alpha}_0(9u_{xxx}-9u_{xxxx}+27uu_{x} +135u_{x}v+3u_{x}+9u_{xx}-18v_{xx}{}\\ &&+45uu_{xx}-54uv-4u-15u^3-18u^2-6v-135v^2-\frac{4}{27})_x. \end{eqnarray} $

本节,我们将通过Darboux变换给出方程(1.1)的一些显式解.该方程所满足的Lax对为如下的矩阵谱问题和辅谱问题

(3.1) $ \begin{eqnarray} \psi_x = U\psi = \left(\begin{array}{cccc} 0&{\quad} u{\quad} &\lambda+v\\ 1&1&0\\ 0&1&0\\ \end{array}\right)\psi, \end{eqnarray} $

(3.2) $ \begin{eqnarray} \psi_t = V^{(0)}\psi = \left(\begin{array}{cccc} -u&{\quad} u_x-3v-3\lambda{\quad} &2u_{xx}-2u_x-3v_x+3v+3\lambda\\ 0&-u&2u_x-3v-3\lambda\\ -3&0&2u\\ \end{array}\right)\psi. \end{eqnarray} $

为了构造方程(1.1)的Darboux变换,我们假设$ \psi^{(l)} = (\psi^{(l)}_1, \psi^{(l)}_2, \psi^{(l)}_3)^T\; (l = 1, 2, 3) $是方程(3.1)和(3.2)的3个解,由此可以定义一个基解矩阵$ \Psi = (\psi^{(1)}, \psi^{(2)}, \psi^{(3)}). $接下来我们引入方程(3.1)和(3.2)的如下的规范变换, $ \Psi \rightarrow \hat\Psi $

(3.3) $ \begin{equation} \hat\Psi = T\Psi = \left(\begin{array}{cccc} T_{11}&T_{12}&T_{13}\\ b_x+c&{\quad} \lambda+c_x+bu+c+d{\quad} &\lambda b+d_x+bv\\ b&c&\lambda+d \end{array}\right)\Psi, \end{equation} $

其中

$ \begin{eqnarray*} && T_{11} = \lambda+b_{xx}+2c_x+bu+d-b_x, \\ &&T_{12} = \lambda b+c_{xx}+2b_xu+bu_x+c_x+2d_x+bv+cu, \\ &&T_{13} = \lambda(2b_x+c-b)+d_{xx}+2b_xv+bv_x+cv-d_x-bv. \end{eqnarray*} $

这里的$ b, c $和$ d $为待定函数.通过复杂的计算可得

(3.4) $ \begin{equation} \det T = \lambda^3+f_1\lambda+f_2, \end{equation} $

其中

$ \begin{eqnarray*} f_1& = &c_xd+bdu+d^2+cd-d_xc-b(d_{xx}+2b_xv+bv_x+2cv-d_x-bv+b_xd+cd-bd_x\\ &&-b^2v) +(b_{xx}+2c_x+bu+d-b_x)(c_x+bu+c+2d-bc)-(b_x+c+b^2)(c_{xx}+c_x\\ & &+2b_xu+bu_x +2d_x+bv+cu)+(2b_x+c-b)(b_xc+c^2-bc_x-b^2u-bc-bd), \\ f_2& = &(d_{xx}+2b_xv+bv_x+cv-d_x-bv)(b_xc-bc_x-b^2u-bc+c^2-bd)\\ &&+(b_{xx}+2c_x+bu+d-b_x)(c_xd+bdu+cd+d^2-d_xc-bcv)\\ &&-(c_{xx}+2b_xu+bu_x+c_x+2d_x+bv+cu)(b_xd+cd-bd_x-b^2v). \end{eqnarray*} $

令$ \lambda_1, \lambda_2, \lambda_3 $是3个给定的任意常数,并且是三次多项式$ \det T $的根,即

(3.5) $ \begin{equation} \det T = (\lambda-\lambda_1)(\lambda-\lambda_2)(\lambda-\lambda_3). \end{equation} $

易知当$ \lambda = \lambda_i\; (i = 1, 2, 3 $)时, $ \hat\Psi $的列向量线性相关.由此,我们得到了下面的线性代数方程组

(3.6) $ \begin{eqnarray} &&\lambda_i+b_{xx}+2c_x+bu+d-b_x+(\lambda_i b+c_{xx}+2b_xu+bu_x+c_x+2d_x+bv+cu)\sigma_1^{(i)}{}\\ &&+[\lambda_i(2b_x+c-b)+d_{xx}+2b_xv+bv_x+cv-d_x-bv]\sigma_2^{(i)} = 0, \end{eqnarray} $

(3.7) $ \begin{equation} b_x+c+(\lambda_i+c_x+bu+c+d)\sigma_1^{(i)}+(\lambda_i b+d_x+bv)\sigma_2^{(i)} = 0, \end{equation} $

(3.8) $ \begin{equation} b+c\sigma_1^{(i)}+(\lambda_i+d)\sigma_2^{(i)} = 0, \end{equation} $

其中

(3.9) $ \begin{equation} \sigma_1^{(i)} = \frac{r_1^{(i)}\psi_2^{(1)}(\lambda_i)+r_2^{(i)}\psi_2^{(2)}(\lambda_i)+r_3^{(i)}\psi_2^{(3)}(\lambda_i)} {r_1^{(i)}\psi_1^{(1)}(\lambda_i)+r_2^{(i)}\psi_1^{(2)}(\lambda_i)+r_3^{(i)}\psi_1^{(3)}(\lambda_i)}, \end{equation} $

(3.10) $ \begin{equation} \sigma_2^{(i)} = \frac{r_1^{(i)}\psi_3^{(1)}(\lambda_i)+r_2^{(i)}\psi_3^{(2)}(\lambda_i)+r_3^{(i)}\psi_3^{(3)}(\lambda_i)} {r_1^{(i)}\psi_1^{(1)}(\lambda_i)+r_2^{(i)}\psi_1^{(2)}(\lambda_i)+r_3^{(i)}\psi_1^{(3)}(\lambda_i)}, \end{equation} $

而$ r_k^{(i)}(k = 1, 2, 3) $是相关系数.直接计算可知,由(3.8)式可以推出(3.7)式,由(3.7)式可以推出(3.6)式.如果合理选择参数$ \lambda_i $和$ r_k^{(i)} $,使得(3.8)式所确定的系数行列式非零,那么$ b, c $和$ d $可以由线性代数系统(3.8)唯一确定.

我们考虑线性变换

(3.11) $ \begin{equation} \hat\psi = T\psi. \end{equation} $

在$ \lambda\not = \lambda_i $的情况下,问题(3.1)和(3.2)可以变换成关于$ \hat\psi $的两个如下的$ 3\times 3 $矩阵谱问题

(3.12) $ \begin{equation} \hat\psi_x = \hat U\hat\psi, \end{equation} $

(3.13) $ \begin{equation} \hat\psi_t = \hat V^{(0)}\hat\psi, \end{equation} $

此处

(3.14) $ \begin{equation} \hat U = (T_x+TU)T^{-1}, \quad \hat V^{(0)} = (T_t+TV^{(0)})T^{-1}. \end{equation} $

可以证明$ \lambda = \lambda_i $是$ \hat U $和$ \hat V^{(0)} $的可去孤立奇点.因此,我们可以借助于解析延拓的办法来定义$ \lambda\not = 0 $时的$ \hat U $和$ \hat V^{(0)} $.

命题3.1  由(3.14)式确定的矩阵$ \hat U $和$ \hat V^{(0)} $与$ U $和$ V^{(0)} $具有相同的形式.特别地,从原始位势$ u, v $到新位势$ \hat u, \hat v $的变换由下式给出

(3.15) $ \begin{equation} \begin{array}{l} \hat u = u+3b_x, \\ \hat v = v+3b_{xx}+3c_x-2b_x-3bb_x. \end{array} \end{equation} $

证  令$ T^{-1} = T^*/\det T $并且

(3.16) $ \begin{equation} (T_x+TU)T^* = F = (f_{sl}(\lambda))_{3\times 3}. \end{equation} $

通过计算,我们可以得到

(3.17) $ \begin{equation} T_x+TU = \left(\begin{array}{cccc} h_{11}&{\quad} h_{12}{\quad} &h_{13}\\ h_{21}&h_{22}&h_{23}\\ h_{31}&h_{32}&h_{33}\\ \end{array}\right), \end{equation} $

其中

$ \begin{eqnarray*} \begin{array}{rl} h_{11} = &\lambda b+b_{xxx}+3c_{xx}+3b_xu+2bu_x+3d_x-b_{xx}+c_x+cu+bv, \\ h_{12} = &\lambda(3b_x+u+c)+(c_{xx}+2b_xu+bu_x+c_x+2d_x+bv+cu)_x\\ &+(b_{xx}+2c_x+bu+d+b_x)u+c_{xx}+bu_x+c_x+d_x+cu+d_{xx}+2b_xv+bv_x+cv, \\ h_{13} = &\lambda^2+\lambda(3b_{xx}+3c_x-2b_x+d+v+bu)+(d_{xx}+2b_xv+bv_x+cv-d_x-bv)_x\\ &+(b_{xx}+2c_x+bu+d-b_x)v, \\ h_{21} = &\lambda+b_{xx}+2c_x+bu+c+d, \\ h_{22} = &\lambda(b+1)+c_{xx}+2b_xu+bu_x+2c_x+2d_x+cu+bu+c+d+bv, \\ h_{23} = &\lambda(2b_x+c)+d_{xx}+2b_xv+bv_x+cv, \\ h_{31} = &b_x+c, \ \ \ \ \ h_{32} = \lambda+c_x+bu+c+d, \ \ \ \ h_{33} = \lambda b+d_x+bv. \end{array} \end{eqnarray*} $

利用(3.9)式, (3.10)式和当$ \lambda = \lambda_i\ (i = 1, 2, 3) $时的谱问题(3.1),我们可以得到两个Riccati方程

(3.18) $ \begin{equation} \begin{array}{l} \sigma_{1, x}^{(i)} = 1+\sigma_1^{(i)}-u(\sigma_1^{(i)})^2-(\lambda_i+v)\sigma_1^{(i)}\sigma_2^{(i)}, \\ \sigma_{2, x}^{(j)} = \sigma_1^{(i)}-u\sigma_1^{(i)}\sigma_2^{(i)}-(\lambda_i+v)(\sigma_2^{(i)})^2. \end{array} \end{equation} $

将(3.8)式关于$ x $求导,我们可以得到(3.7)式;将(3.7)式关于$ x $求导,我们可以得到(3.6)式.

由(3.16)和(3.17)式,我们可以得到

(3.19) $ \begin{equation} (T_x+TU)T^* = (\det T)P(\lambda), \end{equation} $

其中$ P(\lambda) $形式如下

(3.20) $ \begin{equation} P(\lambda) = \left(\begin{array}{cccc} 0&{\quad} p_{12}^{(0)}{\quad} &p_{13}^{(1)}\lambda+p_{13}^{(0)}\\ 1&1&0\\ 0&1&0\\ \end{array}\right). \end{equation} $

这里$ p^{(i)}_{sl}(1\leq s, l\leq3, i = 0, 1) $是与$ \lambda $无关的$ (x, t) $的函数.通过比较(3.19)式中$ \lambda $的同次幂系数,我们可以得到

$ \begin{eqnarray*} p_{12}^{(0)} = 3b_x+u = \hat u, \ \ \ \ \ p_{13}^{(1)} = 1, \ \ \ \ \ p_{13}^{(0)} = v+3b_{xx}+3c_x-2b_x-3bb_x = \hat v, \ \ \ \end{eqnarray*} $

即有$ P(\lambda) = \hat U $.

同理,我们令

(3.21) $ \begin{equation} (T_t+TV^{(0)})T^* = G = (g_{sl}(\lambda))_{3\times 3} \end{equation} $

和$ T_t+TV^{(0)} = M = (m_{sl}(\lambda))_{3\times 3}. $直接计算可得

$ \begin{eqnarray*} m_{11}& = &\lambda(3b-6b_x-u-3c)+(b_{xx}+2c_x+bu+d-b_x)_t-(b_{xx}+2c_x+bu+d-b_x)u\\ &&-3(d_{xx}+2b_xv+bv_x+cv-d_x-bv), \\ m_{12}& = &-3\lambda^2+\lambda(b_t+u_x-3v-3b_{xx}-6c_x-4bu-3d+3b_x)\\ &&+(c_{xx}+2b_xu+bu_x+c_x+2d_x+bv+cu)_t+(b_{xx}+2c_x+d-b_x)(u_x-3v)\\ &&-(c_{xx}+2b_xu+c_x+2d_x+cu+4bv)u, \\ m_{13}& = &3\lambda^2(1-b)+\lambda(2b_{xt}+c_t-b_t+3b_{xx}+3c_x+bu+3d-3b_x+2u_{xx}-3c_{xx}-2u_x\\ &&-3v_x+3v-6bv-2b_xu-bu_x-6d_x-cu)+(d_{xx}+2b_xv+bv_x+cv-d_x-bv)_t\\ &&+(b_{xx}+2c_x+bu+d-b_x)(2u_{xx}-2u_x-3v_x+3v)+(c_{xx}+c_x+bv+cu+bu_x\\ &&+2b_xu+2d_x)(2u_x-3v)+2u(d_{xx}+2b_xv+bv_x+cv-d_x-bv), \\ m_{21}& = &-3\lambda b+b_{xt}+c_t-b_xu-cu-3d_x-3bv, \\ m_{22}& = &-\lambda(3b_x+3c+u)+(c_x+bu+c+d)_t+(b_x+c)(u_x-3v)-u(c_x+bu+c+d), \\ m_{23}& = &-3\lambda^2+\lambda(b_t+3b_x-3c_x-bu-3d+2u_x-3v)+d_{xt}+b_tv+bv_t+2d_xu+2buv\\ &&+(b_x+c)(2u_{xx}-3v_x)+(c_x+bu+d-b_x)(2u_x-3v), \\ m_{31}& = &-3\lambda+b_t-bu-3d, \ \ \ \ \ \ \ m_{32} = -3\lambda b+c_t+bu_x-3bv-cu, \\ m_{33}& = &\lambda(3b-3c+2u)+d_t+2bu_{xx}-2bu_x-3bv_x+3bv+2cu_x-3cv+2du. \end{eqnarray*} $

通过比较(3.21)式中$ \lambda $的同次幂系数,我们可以得到

(3.22) $ \begin{equation} (T_t+TV^{(0)})T^* = (\det T)Q(\lambda), \end{equation} $

其中

(3.23) $ \begin{equation} Q(\lambda) = \left(\begin{array}{cccc} q^{(0)}_{11}&{\quad} q^{(1)}_{12}\lambda+q^{(0)}_{12}{\quad} &q^{(1)}_{13}\lambda+q_{13}^{(0)}\\ 0&q^{(0)}_{22}&q^{(1)}_{23}\lambda+q^{(0)}_{23}\\ -3&0&q^{(0)}_{33} \end{array}\right), \end{equation} $

这里$ q^{(i)}_{sl}(1\leq s, l\leq3) $是与$ \lambda $无关的$ (x, t) $的函数.借助于(3.22)式,直接计算可知

$ \begin{eqnarray*} && q^{(0)}_{11} = -u-3b_x = -\hat u, \ \ \ \ \ \ q^{(0)}_{12} = u_x-3v-6b_{xx}-9c_x+6b_x+9bb_x = \hat u_x-3\hat v, \\ &&q_{13}^{(0)} = 9b_x^2-9bb_x+9bb_{xx}-3b_{xxx}-9c_{xx}+9b_{xx}+9c_x-6b_x+2u_{xx}-2u_x-3v_x+3v\\ &&\ \ \ \ \ \, = 2\hat u_{xx}-2\hat u_x-3\hat v_x+3\hat v, \\ &&q^{(0)}_{22} = -u-3b_x = -\hat u, \ \ \ \ q^{(0)}_{23} = 9bb_x-3b_{xx}-9c_x+6b_x+2u_x-3v = 2\hat u_x-3\hat v , \\ &&q^{(0)}_{33} = 2u+6b_x = 2\hat u, \ \ \ \ \ \ q^{(1)}_{12} = -q_{13}^{(1)} = q^{(1)}_{23} = -3, \end{eqnarray*} $

即证$ Q(\lambda) = \hat V^{(0)} $,证毕.

根据命题3.1,通过变换(3.11)和(3.15),我们把Lax对(3.1)和(3.2)变成了另一个具有相同形式的Lax对

(3.24) $ \begin{equation} \hat\psi_x = \hat U\hat\psi, \end{equation} $

(3.25) $ \begin{equation} \hat\psi_t = \hat V^{(0)}\hat\psi. \end{equation} $

因此,两个Lax对都可以推出方程(1.1).变换(3.15), $ (u, v)\longrightarrow(\hat u, \hat v) $,叫做方程(1.1)的Darboux变换.

定理3.1  Darboux变换(3.15)把方程(1.1)的任一解$ (u, v) $变成一个新解$ (\hat u, \hat v) $,其中$ b, c, d $由方程(3.8)唯一确定.

为了构造方程(1.1)的精确解,我们将方程(3.8)改写为

(3.26) $ \begin{eqnarray} &&b+c\sigma_{1}^{(1)}+d\sigma_{2}^{(1)} = -\lambda_{1}\sigma_{2}^{(1)}, {}\\ &&b+c\sigma_{1}^{(2)}+d\sigma_{2}^{(2)} = -\lambda_{2}\sigma_{2}^{(2)}, \\ &&b+c\sigma_{1}^{(3)}+d\sigma_{2}^{(3)} = -\lambda_{3}\sigma_{2}^{(3)}.{} \end{eqnarray} $

由克莱姆法则得

(3.27) $ \begin{equation} b = \frac{\Delta_1}{\Delta}, \quad c = \frac{\Delta_2}{\Delta}, \quad d = \frac{\Delta_3}{\Delta}, \end{equation} $

其中

$ \Delta = \left|\begin{array}{cccc} 1&{\quad} \sigma_{1}^{(1)}{\quad} &\sigma_{2}^{(1)}\\ 1&\sigma_{1}^{(2)}&\sigma_{2}^{(2)}\\ 1&\sigma_{1}^{(3)}&\sigma_{2}^{(3)}\\ \end{array}\right|, {\quad} \Delta_1 = \left|\begin{array}{cccc} -\lambda_{1}\sigma_{2}^{(1)}&{\quad} \sigma_{1}^{(1)}{\quad} &\sigma_{2}^{(1)}\\ -\lambda_{2}\sigma_{2}^{(2)}&\sigma_{1}^{(2)}&\sigma_{2}^{(2)}\\ -\lambda_{3}\sigma_{2}^{(3)}&\sigma_{1}^{(3)}&\sigma_{2}^{(3)}\\ \end{array}\right|, $

$ \Delta_2 = \left|\begin{array}{cccc} 1&{\quad} -\lambda_{1}\sigma_{2}^{(1)}{\quad} &\sigma_{2}^{(1)}\\ 1&-\lambda_{2}\sigma_{2}^{(2)}&\sigma_{2}^{(2)}\\ 1&-\lambda_{3}\sigma_{2}^{(3)}&\sigma_{2}^{(3)}\\ \end{array}\right|, {\quad} \Delta_3 = \left|\begin{array}{cccc} 1&{\quad}\sigma_{1}^{(1)}{\quad}&-\lambda_{1}\sigma_{2}^{(1)}\\ 1&\sigma_{1}^{(2)}&-\lambda_{2}\sigma_{2}^{(2)}\\ 1&\sigma_{1}^{(3)}&-\lambda_{3}\sigma_{2}^{(3)}\\ \end{array}\right|. $

合理选择$ \lambda_1, \lambda_2, \lambda_3, r_1^{(1)}, r_2^{(1)}, r_3^{(1)}, r_1^{(2)}, r_2^{(2)}, r_3^{(2)}, r_1^{(3)}, r_2^{(3)}, r_3^{(3)} $使得系数行列式$ \Delta\not = 0. $把(3.27)式代入(3.15)式,我们可以得到Darboux变换的显式形式

(3.28) $ \begin{equation} \hat u = u+3\left(\frac{\Delta_1}{\Delta}\right)_x, \quad\hat v = v+3\left(\frac{\Delta_1}{\Delta}\right)_{xx}+3\left(\frac{\Delta_2}{\Delta}\right)_x -2\left(\frac{\Delta_1}{\Delta}\right)_x-3\left(\frac{\Delta_1}{\Delta}\right)\left(\frac{\Delta_1}{\Delta}\right)_x. \end{equation} $

接下来,我们将应用Darboux变换来构造方程(1.1)的显式解.

1)取$ u = -\frac{1}{3}, \ v = \frac{1}{27} $,则(3.1)和(3.2)式可表示为

(3.29) $ \begin{equation} \left\{\begin{array}{l} { } \psi_{1, x} = -\frac{1}{3}\psi_{2}+(\lambda+\frac{1}{27})\psi_{3}, \\ { } \psi_{2, x} = \psi_1+\psi_2, \\ { } \psi_{3, x} = \psi_2, \\ { } \psi_{1, t} = \frac{1}{3}\psi_{1}+(-\frac{1}{9}-3\lambda)\psi_{2}+(\frac{1}{9}+3\lambda)\psi_{3}, \\ { } \psi_{2, t} = \frac{1}{3}\psi_{2}+(-\frac{1}{9}-3\lambda)\psi_{3}, \\ { } \psi_{3, t} = -3\psi_1-\frac{2}{3}\psi_{3}. \end{array}\right. \end{equation} $

从而方程(3.29)有基础矩阵

(3.30) $ \begin{equation} \Psi = \left(\begin{array}{cccc} { } (\eta^2-\frac{1}{3}\eta-\frac{2}{9})e^M&\ e^Q(n_1\cos N+n_2\sin N)\ &e^Q(n_1\sin N-n_2\cos N)\\ { } (\frac{1}{3}+\eta)e^M&\begin{array}{c} { } \{e^Q[(\frac{1}{3}-\frac{1}{2}\eta)\cos N\\ { } -\frac{\sqrt3}{2}\eta\sin N]\}\end{array}& \begin{array}{c} { } \{e^Q[(\frac{1}{3}-\frac{1}{2}\eta)\sin N\\ { } +\frac{\sqrt3}{2}\eta\cos N]\}\end{array}\\ e^M&e^Q\cos N&e^Q\sin N \end{array}\right), \end{equation} $

其中

$ \eta = \lambda ^{1/3}, \ \ n_1 = -\frac{1}{2}\eta^2+\frac{1}{6}\eta-\frac{2}{9}, \ \ n_2 = \frac{\sqrt3}{2}\eta^2+\frac{\sqrt3}{6}\eta, \ \ M = (\frac{1}{3}+\eta)x-(3\eta^2-\eta)t, $

$ N = \frac{\sqrt3}{2}\eta x+\frac{\sqrt3}{2}(3\eta^2+\eta)t, \ \ Q = (\frac{1}{3}-\frac{1}{2}\eta))x+\frac{1}{2}(3\eta^2-\eta)t. $

由(3.9)和(3.10)式可得

$ \sigma_1^{(i)} = \frac{r_1^{(i)}(6+18\eta)e^{M-Q}+[r_2^{(i)}(6-9\eta)+9\sqrt 3\eta r_3^{(i)}]\cos N+[r_3^{(i)}(6-9\eta)-9\sqrt 3\eta r_2^{(i)}]\sin N} {r_1^{(i)}(18\eta^2-6\eta-4)e^{M-Q}+(18n_1r_2^{(i)}-18n_2r_3^{(i)})\cos N+(18n_2r_2^{(i)}+18n_1r_3^{(i)})\sin N}, $

$ \sigma_2^{(i)} = \frac{18r_1^{(i)}e^{M-Q}+18r_2^{(i)}\cos N+18r_3^{(i)}\sin N} {r_1^{(i)}(18\eta^2-6\eta-4)e^{M-Q}+(18n_1r_2^{(i)}-18n_2r_3^{(i)})\cos N+(18n_2r_2^{(i)}+18n_1r_3^{(i)})\sin N}. $

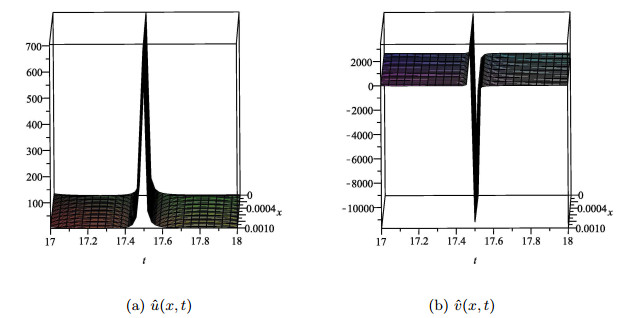
通过Darboux变换(3.15),我们得到方程(1.1)的一个显式解

(3.31) $ \begin{eqnarray} \hat u& = &3\frac{{\Delta_{1, x}}\Delta-{\Delta_1\Delta_x}}{\Delta^2}, {}\\ \hat v& = &\frac{3\Delta_{1, xx}+3\Delta_{2, x}-2\Delta_{1, x}}{\Delta}+3\frac{{2\Delta_x}^2\Delta_1+{\Delta_1}^2\Delta_x}{\Delta^3}-\lambda{}\\ &&+\frac{2\Delta_1\Delta_x -3\Delta_2\Delta_x-3\Delta_1\Delta_{1, x}-6\Delta_{1, x}\Delta_x-3\Delta_1\Delta_{xx}}{\Delta^2}. \end{eqnarray} $

2)取$ u = 0, \ v = 0 $,则(3.1)和(3.2)式可表示为

(3.32) $ \begin{equation} \left\{\begin{array}{c} \psi_{1, x} = \lambda\psi_3, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \psi_{2, x} = \psi_1+\psi_2, \ \ \ \psi_{3, x} = \psi_2, \ \ \\ \psi_{1, t} = -3\lambda(\psi_2-\psi_3), \ \ \psi_{2, t} = -3\lambda\psi_3, \ \ \ \ \psi_{3, t} = -3\psi_1. \end{array}\right. \end{equation} $

此时方程(3.32)有基解矩阵

(3.33) $ \begin{equation} \Psi = \left(\begin{array}{cccc} (k_1^2-k_1)e^{\Gamma_1}&\psi_1^{(2)} &\psi_1^{(3)}\\ k_1e^{\Gamma_1}&\psi_2^{(2)}&\psi_2^{(3)}\\ e^{\Gamma_1}&\ e^{\Gamma_2}{\rm cos}{\Gamma_3}\ &e^{\Gamma_2}{\rm sin}{\Gamma_3} \end{array}\right), \end{equation} $

其中

$ \psi_1^{(2)} = \frac{1}{9}e^{\Gamma_2}[(k_2^2-k_3^2-3k_2){\rm cos}{\Gamma_3}-(2k_2k_3-3k_3){\rm sin}{\Gamma_3}], \ \psi_2^{(2)} = \frac{1}{3}e^{\Gamma_2}(k_2{\rm cos}{\Gamma_3}-k_3{\rm sin}{\Gamma_3}), $

$ \psi_1^{(3)} = \frac{1}{9}e^{\Gamma_2}[(k_2^2-k_3^2-3k_2){\rm sin}{\Gamma_3}+(2k_2k_3-3k_3){\rm cos}{\Gamma_3}], \ \psi_2^{(3)} = \frac{1}{3}e^{\Gamma_2}(k_2{\rm sin}{\Gamma_3}+k_3{\rm cos}{\Gamma_3}), $

$ \Gamma = (\frac{2}{2+27\lambda+3\sqrt{12\lambda+81\lambda^2}})^{\frac{1}{3}}, \ \ k_1 = \frac{1}{3}(1+\Gamma+\frac{1}{\Gamma}), \ \ k_2 = 1-\frac{\Gamma}{2}-\frac{1}{2\Gamma}, $

$ k_3 = -\frac{\sqrt{3}}{2}(\Gamma-\frac{1}{\Gamma}), {\quad} \Gamma_1 = \frac{1}{3}(1+\Gamma+\frac{1}{\Gamma})x-\frac{1}{3}(\Gamma-1)(\Gamma-\frac{1}{\Gamma^2})t, $

$ \Gamma_2 = \frac{1}{3}k_2x-\frac{1}{3}(k_2^2-k_3^2-3k_2)t, \ \ \Gamma_3 = \frac{1}{3}k_3x-\frac{1}{3}(2k_2k_3-3k_3)t, $

由(3.9)和(3.10)式可得

$ \sigma_1^{(i)} = \frac{r_1^{(i)}k_1e^{\Gamma_1}+r_2^{(i)}\psi_2^{(2)}+r_3^{(i)}\psi_2^{(3)}} {r_1^{(i)}(k_1^2-k_1)e^{\Gamma_1}+r_2^{(i)}\psi_1^{(2)}+r_3^{(i)}\psi_1^{(3)}}, $

$ \sigma_2^{(i)} = \frac{r_1^{(i)}e^{\Gamma_1}+r_2^{(i)}e^{\Gamma_2}{\rm cos}{\Gamma_3}+r_3^{(i)}e^{\Gamma_2}{\rm sin}{\Gamma_3}} {r_1^{(i)}(k_1^2-k_1)e^{\Gamma_1}+r_2^{(i)}\psi_1^{(2)}+r_3^{(i)}\psi_1^{(3)}}. $

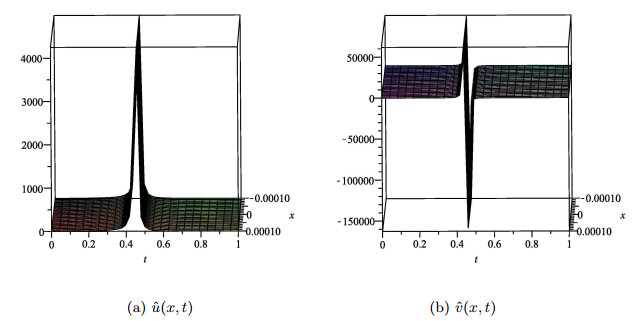
通过Darboux变换(3.15),我们得到方程(1.1)的显式解

(3.34) $ \begin{eqnarray} \hat u& = &3\frac{{\Delta_{1, x}}\Delta-{\Delta_1\Delta_x}}{\Delta^2}, {}\\ \hat v& = &\frac{3\Delta_{1, xx}+3\Delta_{2, x}-2\Delta_{1, x}}{\Delta}+3\frac{{2\Delta_x}^2\Delta_1+{\Delta_1}^2\Delta_x}{\Delta^3}{}\\ && \qquad+\frac{2\Delta_1\Delta_x -3\Delta_2\Delta_x-3\Delta_1\Delta_{1, x}-6\Delta_{1, x}\Delta_x-3\Delta_1\Delta_{xx}}{\Delta^2}. \end{eqnarray} $