1 引言
1908年法国物理学家Langevin在研究布朗运动时提出:溶液中介质分子对布朗粒子的作用力可分为两个部分,一部分是流体对布朗粒子的黏滞阻力,另一部分是溶液分子无规则热运动施加在布朗粒子上的一种涨落不定的力.由此, Langevin在牛顿第二定律的基础上提出Langevin方程[1]
其中,
在各类数值解法中,显式算法计算过程较为简便,但精度比较差,稳定性不好,隐式算法虽然提高了精度,但算法复杂,计算量大.文献[10]预估校正算法在结合了两者的优点基础上,同时简化了算法的计算量.文献[11]提出的用预估校正Euler方法来求解随机微分方程,该方法能克服使用显式欧拉方法时经常遇到的一些数值不稳定性,数值实验证明了其提出的对称预估校正欧拉方法的渐近稳定性.文献[12]采用路径逼近的方法,建立了用马尔可夫切换求解随机微分方程的数值方法,并且用预测校正Euler-Maruyama方法来克服近似路径模拟过程中的误差传播,证明了数值解对精确解的强收敛性,并揭示了在一定条件下误差在系数函数上的有序性.文献[13]将预估校正算法运用于Itô型随机微分方程,推导出预估校正方法的稳定性条件,证明在适当的条件下,预估校正方法对于所有非常小的时间步长保持时间指数稳定性.文献[14]针对Itô型随机延迟微分方程,在Lipschitz和线性增长条件下,预估校正方法被证明是min
本文尝试用预估校正算法来求解分数阶Langevin方程.将(1.1)式中质量
2 分数阶Langevin方程预估校正算法
或
利用R2算法将Caputo积分离散化,其中, R2算法(参见文献[18])
得到
其中,系数
差分逼近格式(2.3)式称为分数阶Adams-Moulton方法,等号右边的
其中
将(2.4)式代入(2.3)式右边,得到(1.2)式分数阶Langevin方程的预估校正算法
3 预估校正算法的误差分析
引理3.1 假设
证 因为
所以有
由中值定理及
由于
所以
引理3.1得证.
引理3.2 假设
证 过程与引理3.1证明类似.
定理3.1 当
其中
证 令
先考察预估值
由
对校正误差进行分析
由预估值
因此,定理3.1得证.
4 数值试验
考虑如下分数阶Langevin方程[2]
用方程的逆拉普拉斯变换,得到分数阶Langevin方程的一般解为[1]
其中, Mittag-Leffler函数表示为
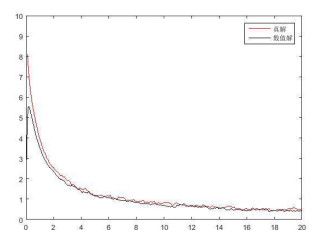
图 1
图 2
图 3
图 4
图 5
为了削弱随机项对数值解的影响,得到的数值解是由50条样本轨迹取均值来表现的,而真值则由随机得到的某一条轨迹来表示.通过得到的真值和数值解的比较图形可以看出,数值解与真值趋势相同,且始终在真值附近波动.
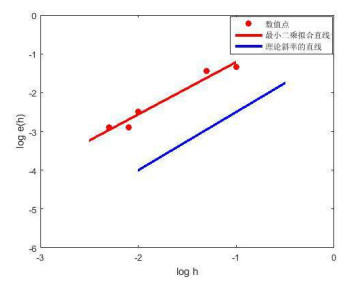
进一步,用数值算例结果证明预估校正算法数值解误差的收敛阶.设收敛阶为
记误差
就有
在两边同时取对数变形为
数值算例已经得到不同
表 1 真解和预估校正算法数值解的误差及收敛阶
| 0.005 | 0.0034 | 0.005 | 0.0010 | ||||
| 0.008 | 0.0105 | 0.008 | 0.0028 | ||||
| 0.1 | 0.01 | 0.0117 | 1.0732 | 0.3 | 0.01 | 0.0026 | 1.2005 |
| 0.05 | 0.0638 | 0.05 | 0.0635 | ||||
| 0.1 | 0.0941 | 0.1 | 0.018 | ||||
| 0.005 | 0.0013 | 0.005 | 0.0012 | ||||
| 0.008 | 0.0013 | 0.008 | 0.0022 | ||||
| 0.5 | 0.01 | 0.0032 | 1.3476 | 0.7 | 0.01 | 0.0041 | 1.5506 |
| 0.05 | 0.0364 | 0.05 | 0.0578 | ||||
| 0.1 | 0.0462 | 0.1 | 0.1037 | ||||
| 0.005 | 0.0006 | ||||||
| 0.008 | 0.0007 | ||||||
| 0.9 | 0.01 | 0.0015 | 1.8435 | ||||
| 0.05 | 0.0478 | ||||||
| 0.1 | 0.0850 |
在每一个
图 6
固定
图 7
5 结论
本文针对一类分数阶Langevin方程,利用预估校正算法对其进行数值求解.利用R2算法,求解
参考文献
Fractional Langevin model of memory in financial markets
Fractional Langevin model of memory in financial time series
Generalized Langevin equation with fractional derivative and long-time correlation function
Fractional Langevin equation and Riemann-Liouville fractional derivative
DOI:10.1140/epje/i2007-10224-2 [本文引用: 1]
Fractional brownian motion and motion governed by the fractional Langevin equation in confined geometries
Fractional Langevin equation
DOI:10.1103/PhysRevE.64.051106 [本文引用: 1]
Solution of the fractional Langevin equation and the Mittag-Leffler functions
A shifted Jacobi-Gauss-Lobatto collocation method for solving nonlinear fractional Langevin equation involving two fractional orders in different intervals
A predictor-corrector approach for the numerical solution of fractional differential equations
Strong predictor-corrector Euler methods for stochastic differential equations
Strong predictor-corrector Euler-Maruyama methods for stochastic differential equations with Markovian switching
Almost sure and moment exponential stability of predictor-corrector methods for stochastic differential equations
Strong predictor-corrector approximation for stochastic delay differential equations
Strong predictor-corrector methods for stochastic pantograph equations
Linearly implicit predictor-corrector methods for space-fractional reaction-diffusion equations with non-smooth initial data
DOI:10.1016/j.camwa.2017.12.033 [本文引用: 1]
Analysis of fractional differential equations
Detailed error analysis for a fractional adams method
时间分数阶慢扩散方程的一类有效差分方法
DOI:10.3969/j.issn.1003-3998.2018.06.009 [本文引用: 1]
A kind of efficient difference method for the time fractional sub-diffusion equation
DOI:10.3969/j.issn.1003-3998.2018.06.009 [本文引用: 1]
Stochastic calculus for fractional brownian motion and applications