1 引言
最近几年,比例时滞(或称缩放时滞)神经网络引起了部分学者的关注[12-21]. 2014年, Zhou在文献[14]中分析了具有比例时滞的细胞神经网络平衡点的唯一性和全局渐近稳定性,利用矩阵理论,通过构造适当的李雅普诺夫泛函,得到了具有比例时滞的细胞神经网络全局渐近稳定性的时滞相关和时滞无关的充分条件; 2016年, Liu在文献[17]中研究了一类多比例时滞非自治细胞神经网络的指数收敛问题.利用微分不等式分析方法,得到了系统的所有解都以指数形式收敛于零向量的充分条件; 2017年, Xu等人在文献[20]利用微分不等式分析技巧,得出了一类具有多比例时滞和泄漏时滞的中立型Hopfield神经网络的所有解指数收敛于零向量的充分条件; 2018年, Cui等人在文献[21]利用线性矩阵不等式,构造适当的李雅普诺夫泛函的方法,得出了一类具有比例时滞的惯性神经网络的全局渐近稳定性的几个充分条件.这些文献有的是利用构造李亚普诺夫函数(简称V函数)方法来分析神经网络的稳定性问题(尤其是全局渐近稳定性),这是十分经典的方法,但是这一方法的困难在于构造V函数没有一般的规律,技巧性较强,需要靠一定的经验积累;对于指数稳定性问题,这些文献是利用微分不等式技巧方法来进行分析,结论和证明过程都比较复杂.而Gronwall积分不等式[25]在微分方程定性理论研究中也发挥极其重要的作用,恰当的使用将会使得问题的分析过程变得更加简单,因而得到不断的推广和广泛应用[26-29].
本文基于以上文献的研究,利用Gronwall积分不等式研究如下Hopfield放缩时滞神经网络模型的稳定性问题,得到十分简洁的证明过程和结果.
其中
这里我们定义
现设每一个激活函数
引理1.1 如果
证 如果
因为
(1.3)式的矩阵形式表示为
记
为了证明(1.5)式成立,做映射
由已知条件,
记
则
下面证明平衡点是唯一的.
假设另有
即
由前面的证明知
设系统(1.1)的平衡点为
其中,
引理1.2 (Gronwall不等式)[25] 设K为非负常数,
则有
2 稳定性分析
为了获得时滞情形的结果,我们先来分析无时滞的情形:
系统(2.1)的线性系统为
线性系统(2.2)的基解矩阵为
当
取范数
为了方便,做以下记号:
(Ⅰ)
(Ⅱ)
于是可得
定理2.1 激活函数
证 设
其中
两边同时乘以
根据引理1.2(Gronwall不等式)得
两边同时除以
现在我们来分析具有时滞的情况,对于系统(1.7),我们有如下定理:
定理2.2 激活函数
证 当
因为
两边同时乘以
根据引理1.2(Gronwall不等式)得
所以
由于
3 数值仿真
这一节,我们用一个实际例子来验证定理结果的有效性.
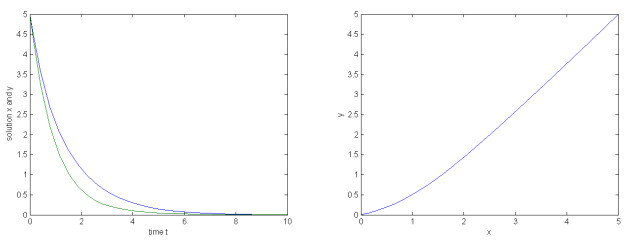
例1 考虑如下无时滞二维神经网络模型:
其中,激活函数
图 1
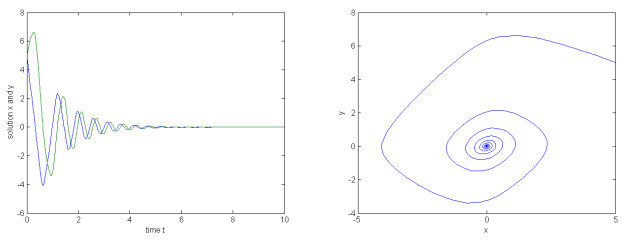
如果我们取
图 2
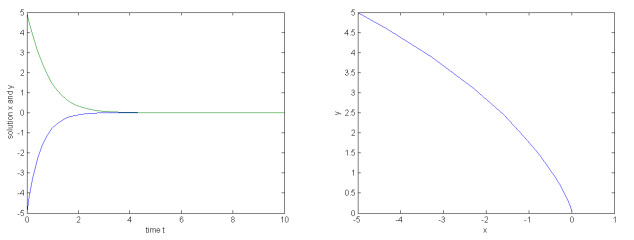
例2 考虑如下具有比例时滞的二维神经网络模型:
其中,激活函数
图 3
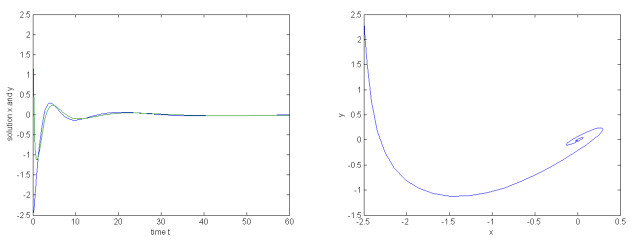
如果我们取\boldsymbol{A}= \left[\begin{array}{cc}2&0\\0&2\end{array}\right], \boldsymbol{B}=\left[\begin{array}{cc}1.7&1\\3.5&-1.4\end{array}\right], \boldsymbol{C}= \left[\begin{array}{cc}1.8&-3\\2&-1.3\end{array}\right],放缩时滞比例系数\tau=0.7,那么, \sigma=2, \| \boldsymbol{B}\|=5.2, \| \boldsymbol{C}\|=4.3, L(\| \boldsymbol{B}\|+\tau^{-1}\| \boldsymbol{C}\|)(1+\tau)-\sigma \approx 7.6414>0,当t=0时,初值取(x(0), y(0))^T=(2.5, -2.5)^T,系统状态轨线图如图 4所示,显然此时系统(3.2)是稳定的,但不是指数稳定的.
图 4
图 4
系统(3.2)的状态轨线图(L(\| \boldsymbol{B}\|+\tau^{-1}\| \boldsymbol{C}\|)(1+\tau)-\sigma>0)
参考文献
Global stability and local stability of Hopfield neural networks with delays
DOI:10.1103/PhysRevE.50.4206 [本文引用: 2]
Stability of analog neural networks with delay
Stability of Hopfield-type neural networks Ⅱ
Stability analysis of delayed cellular neural networks
DOI:10.1016/S0893-6080(98)00080-X
Global attractivity in delayed Hopfield neural network models
Periodic oscillation and exponential stability of delayed CNNs
Global dynamics of Hopfield neural networks involving variable delays
DOI:10.1016/S0898-1221(01)00128-6
An estimation of upperbound of delays for global asymptotic stability of delayed Hopfield neural networks
Stability analysis of Hopfield neural networks with time delay
Hopf bifurcation and stability analysis on discrete-time Hopfield neural network with delay
DOI:10.1016/j.nonrwa.2006.09.005
New sufficient conditions for global stability of neutral-type neural networks with time delays
DOI:10.1016/j.neucom.2012.05.016 [本文引用: 1]
Dissipativity of a class of cellular neural networks with proportional delays
DOI:10.1007/s11071-013-0912-x [本文引用: 1]
Asymptotic stability of cellular neural networks with multiple proportional delays
Global asymptotic stability of cellular neural networks with proportional delays
Matrix measure based stability criteria for high-order neural networks with proportional delay
DOI:10.1016/j.neucom.2014.09.016
Finite-time stability of a class of non-autonomous neural networks with heterogeneous proportional delays
Global exponential convergence of non-autonomous cellular neural networks with multi-proportional delays
DOI:10.1016/j.neucom.2016.01.046 [本文引用: 1]
Exponential stability of pseudo almost periodic solutions for cellular neural networks with multi-proportional delays
Global exponential stability of a class of impulsive recurrent neural networks with proportional delays via fixed point theory
DOI:10.1016/j.jfranklin.2015.10.021
Global exponential convergence of neutral-type Hopfield neural networks with multi-proportional delays and leakage delays
DOI:10.1016/j.chaos.2017.01.012 [本文引用: 1]
Global asymptotic and robust stability of inertial neural networks with proportional delays
DOI:10.1016/j.neucom.2017.07.001 [本文引用: 2]
Global power-rate synchronization of chaotic neural networks with proportional delay via impulsive control
DOI:10.1016/j.neucom.2018.01.027
一类新的变时滞中立型神经网络的全局渐近稳定性条件
DOI:10.3969/j.issn.1003-3998.2015.03.017
Note on the derivatives with respect to a parameter of the solutions of a system of differential equations
The stability of solutions of linear differential equations
DOI:10.1215/S0012-7094-43-01059-2 [本文引用: 1]
A retarded Gronwall-like inequality and its applications
On some new integral inequalities of Gronwall-Bellman-Pachpatte type
Nonlinear retarded integral inequalities of type and applications