1 引言
FPE准则直接源于模型的实际应用,为选择AR模型的阶数奠定了理论基础,也是产生AIC准则的基础. AIC准则是计量经济学中重要的信息判断准则,同时在其它领域中也有广泛应用.在AIC准则出现之前,模型选择通过似然函数最大判断模型最优,但是似然函数越大代表参数个数越多, AIC准则结合熵原理和K-L距离解决了这个问题,达到了模型拟合精度和参数个数的平衡.许多学者在后续研究中发现AIC准则在大样本下效果不佳,又引入BIC准则.
本文针对低阶AR模型,引入一种估计模型信噪比的方法,并以该信噪比作为评价AIC、BIC和FPE三种定阶准则准确度的标准,最后提出了一种基于模型信噪比选择定阶方法的方案.实验采用高斯白噪声作为平稳AR模型的输入噪声,研究了在不同的噪声标准差,模型序列长度和特征根等因素影响下,利用AIC、BIC和FPE准则定阶,其准确率与模型信噪比的变化趋势.经过实验得出的结论为:当模型的
2 AR模型与定阶方法简介
2.1 AR模型简介
设
假设
其中
对于一个AR(p)模型:
设
2.2 定阶方法
AIC准则是基于对数似然函数的一种方法,它是拟合精度和参数个数的加权函数,从本质上也反映了真实模型拟合的准确性与实际处理量之间的综合考虑.
其中,
BIC准则弥补了当样本量趋于无穷大时, AIC准则所选模型不收敛于真实模型的不足.模型的BIC函数为
与AIC函数相比,上述公式右边的第二项用
FPE准则的基本思路是根据模型的预报误差来判断自回归模型的阶数是否合适.如果某个适用的自回归模型是由某一序列拟合得来,则利用该模型对该序列进行一步预测,所得的预测误差必定是最小的,因此,预测效果的好坏,反过来也可作为模型拟合优劣的检验准则. FPE准则定义为
在所有通过检验的模型中使AIC、BIC或FPE函数达到最小的模型为相对最优模型.由于无法比较所有模型的函数值,只能在尽量全面的范围内检查有限数量模型的函数值,并需要预先指定阶数的最大范围,因此本文取
3 信噪比的选择
比较定阶方法的优劣可以从四个方面考虑:准确度、稳健性、计算速度和简单性,其首要指标就是准确度,而衡量“准”的标准至关重要.对于同一组数据,使用不同定阶准则得到的阶数可能不一致,而评估不同定阶方法准确度的标准,需要综合考虑噪声标准差、模型序列长度和特征根等因素的影响.在有噪声的时序分析中,我们关心的一个重要参数是信噪比,它是模型选择的有效指标,引入信噪比评价各种定阶准则的准确度,可以自适应的采用更有效的方法来定阶.
在通信系统中常采用信噪比作为度量信道质量的参量,它是通信系统中的一个重要指标,保持一个合理的信噪比非常重要.信噪比定义为信号功率与噪声功率的比率,一般以分贝
其中,
大部分情况下,噪声都是加性,而加性噪声中最常见的是高斯白噪声,该噪声信号为一种便于分析的理想噪声信号,因此一般假设系统所产生的噪声或受到的噪声信号干扰是高斯白噪声,也将其作为本文研究的噪声信号.如果信噪比不是恒定的,各种定阶方法都需要信噪比的先验知识才能获得最佳性能,选择一种精度高、分辨能力好、计算简单的信噪比估计方法尤为重要.
信噪比估计的研究较多,其性能优劣,不可一概而论,大致可以分为时域方法和频域方法.大部分时域方法适用于具有一定包络线的输入信号,而AR模型没有确定的包络,所以一些经典的信噪比估计方法不适用于这里的输入信号.本文利用白丹萍在万群指导下提出的方法估计AR模型信噪比[9],该方法充分利用了AR模型的信息,能很好地反映模型的信噪比随噪声标准差、特征值和序列长度变化的趋势,并且克服了经典频域方法会过低估计SNR值的缺点,其估计SNR的公式为
其中
对于一个
解该矩阵,即得AR模型参数的估计值
选取以下方程组中的任意一个方程
可以计算出噪声方差
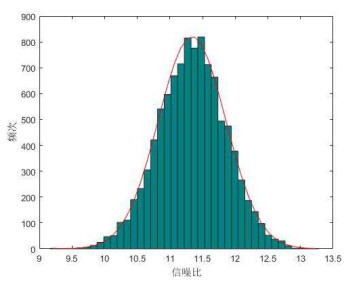
图 1以AR(2)模型为例,令
图 1
表 1
AIC:不同
| 序列长度 | ||||||
| 准确率(%) | 信噪比 | 准确率(%) | 信噪比 | 准确率(%) | 信噪比 | |
| 300 | 62.0 | 36.831 | 88.4 | 38.611 | 90.5 | 41.012 |
| 400 | 73.8 | 36.838 | 90.6 | 38.627 | 91.2 | 41.038 |
| 500 | 81.5 | 36.842 | 90.8 | 38.642 | 91.1 | 41.064 |
| 600 | 85.2 | 36.862 | 91.3 | 38.648 | 90.8 | 41.072 |
| 700 | 87.6 | 36.864 | 91.3 | 38.656 | 91.0 | 41.078 |
表 2
BIC:不同
| 序列长度 | ||||||
| 准确率(%) | 信噪比 | 准确率(%) | 信噪比 | 准确率(%) | 信噪比 | |
| 300 | 18.0 | 36.831 | 73.5 | 38.611 | 99.4 | 41.012 |
| 400 | 27.6 | 36.838 | 88.9 | 38.627 | 99.9 | 41.038 |
| 500 | 38.6 | 36.842 | 95.7 | 38.642 | 100.0 | 41.064 |
| 600 | 50.2 | 36.862 | 98.4 | 38.648 | 100.0 | 41.072 |
| 700 | 60.9 | 36.864 | 99.5 | 38.656 | 100.0 | 41.078 |
4 实验步骤
为进一步研究在噪声标准差、序列长度和特征根等因素的影响下,模型的信噪比与定阶准确率之间的关系,设计以下实验,依据实验结果分别得到信噪比和定阶准确率随这些因素变化的趋势,并尝试以这些因素为转换量建立信噪比与定阶准确率的关系.
(1)构造平稳低阶AR(p)模型
设
即可构造中心化的AR(p)模型:
其中
(2)产生噪声信号
首先产生一组服从正态分布
(3)计算信噪比
利用以上估计AR模型信噪比的方法计算在确定噪声标准差
(4)计算定阶准确率
分别使用AIC、BIC和FPE准则,在与步骤(3)相同
(5)实验结果
记录在其变化范围内,不同的
5 实验结果与分析
对于AR(p)模型
图 2是以AR(3)模型为例,在
图 2
图 3
如果模型有
5.1 定阶准确率与\sigma_{v}
由以上的结论,可以取AR(p)模型的
图 4以AR(2)为例,
图 4
5.2 定阶准确率与\left|\lambda_{\max}\right| T
利用5.1节中的结论:噪声标准差对定阶准确率影响不大,可以保持
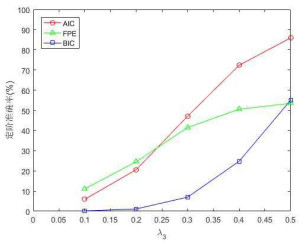
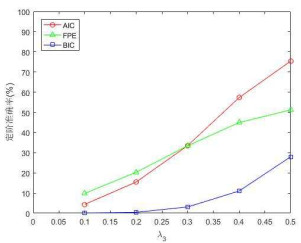
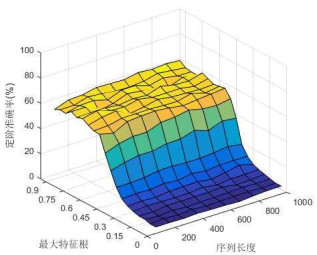
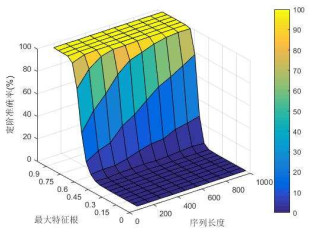
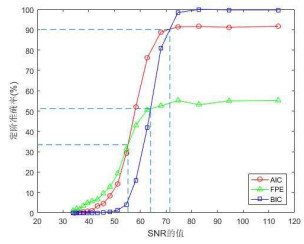
图 5、图 6和图 7分别为使用AIC、FPE和BIC准则,以AR(4)模型为例,其定阶准确率随
图 5
图 6
图 7
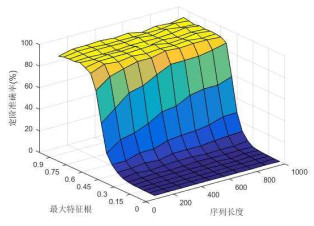
5.3 SNR与\left|\lambda_{\max}\right| T
由于定阶准确率与噪声标准差无关,可以保持
图 8
6 利用SNR选择定阶方法
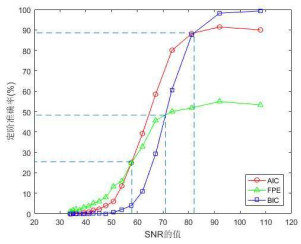
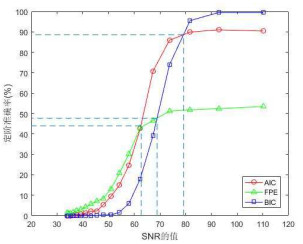
由第5节中的结论:当模型的
图 9
图 10
图 11
图 12
在表 3至表 5中, AIC、BIC和FPE分别缩写为A、B、F,保持
表 3
| 准确度 | AR(2) | AR(3) | AR(4) | AR(5) | ||||
| 上界 | 下界 | 上界 | 下界 | 上界 | 下界 | 上界 | 下界 | |
表 4
| 准确率 | AR(2) | AR(3) | AR(4) | AR(5) | ||||
| 上界 | 下界 | 上界 | 下界 | 上界 | 下界 | 上界 | 下界 | |
表 5
| 准确率 | AR(2) | AR(3) | AR(4) | AR(5) | ||||
| 上界 | 下界 | 上界 | 下界 | 上界 | 下界 | 上界 | 下界 | |
对于任意一个AR模型的定阶方法选择问题,根据以上的结论提出一种利用信噪比选择合适定阶方法的方案.其步骤如下:
(1)已知带有噪声的AR模型序列长度为
(2)设观测值拟合为AR(p)模型(
(3)记录在不同阶数的AR(p)模型和
在实际应用中,例如功能性磁共振成像(Functional Magnetic Resonance Imaging, fMRI), fMRI数据包含噪声并且序列长度较短.假设已知一组fMRI数据,序列长度为200,利用第3节的方法估计其信噪比
7 方法有效性
为验证以上提出的方法是否可行,设计以下实验过程.保持
对于不同阶数的AR模型,在保持与上述相同
8 总结
AR模型是线性时间序列分析中最简单的模型,有限阶的AR模型已经广泛地应用于科研和生产中,所以讨论AR模型具有重要的实际意义.本文综合考虑了噪声标准差、模型序列长度和特征根对定阶准确率的影响,引入一种估计模型信噪比的方法,并以该信噪比作为评价AIC、BIC和FPE三种定阶方法准确度的标准.经过实验得出的结论如下:随着信噪比的增大,定阶准确率越高,而由于定阶方法性能的制约,准确率最终会趋于平稳;当模型的
参考文献
Wavelet neural network classification of EEG signals by using AR model with MLE preprocessing
DOI:10.1016/j.neunet.2005.01.006 [本文引用: 1]
Forecasting traffic time series with multivariate predicting method
DOI:10.1016/j.amc.2016.07.017 [本文引用: 1]
New autoregressive (AR) order selection criteria based on the prediction error estimation
DOI:10.1016/j.sigpro.2011.04.021 [本文引用: 1]
Methods for determining the order of an autoregressive-moving average process:A survey
A comparison of the Akaike and Schwarz criteria for selecting model order