2019年12月,武汉市多个医院报告了不明原因重症肺炎聚集性病例事件,中国政府核实后通报了世界卫生组织(WHO). 2020年1月31日,世界卫生组织将“新型冠状病毒疫情”列为国际关注的突发公共卫生事件(PHEIC).随后新型冠状病毒(SARS-Cov-2)在全球多个国家检测,截止2020年2月20日,新冠病毒已经导致75465人感染,疑似5206人,死亡2236人,治愈18264人,人数已经远超2003年的SARS,参见文献[1-2].

在这次全球新冠肺炎(COVID-19)爆发的疫情中,同样备受关注的有停靠在日本的“钻石公主号”邮轮病毒传播事件.钻石公主号邮轮搭载有2666名乘客和1045名船员, 2020年1月25日,邮轮上一名80岁的乘客在香港下船,随后出现发烧症状, 2月1日被确诊为新型冠状病毒肺炎. 2月15日,新增67名新型冠状病毒肺炎确诊病例,其中38人没有任何症状.截至2月18日,已经确诊感染新型冠状病毒肺炎总数达543例,参见文献[3].

钻石公主号邮轮没有新的外来传染源,病毒在船中递次传染,明确的病源只有一个人,在近一个月时间里,在已经有相应隔离措施的情况下,却发生了如此大规模的流行和传染,显示出病毒强大的传播能力,远远超出直接接触传染途径和近距离飞沫传染范围.由于钻石公主号邮轮在海上漂浮,可以看作是新型冠状病毒(SARS-Cov-2)在封闭空间环境下传播的实验模型.下面我们通过传染病动力学的方法对病毒在邮轮上传播进行简单建模和分析,并结合理论分析和数值预测,对新冠肺炎的传播和防控提出对应策略和建议,这些结论也适用于其他封闭空间环境的场所.

传染病动力学是对传染病的流行规律进行理论性定量研究的一种重要方法,它根据人群特征进行分类,疾病发生和在人群内传播的规律以及与之有关的社会环境等因素,建立能反映传染病动力学特征的数学模型,通过对模型动力学性态的定性、定量分析和数值模拟,来显示疾病的发展过程,揭示其流行规律,预测其变化和发展趋势,分析疾病流行的原因和关键因素,寻找对其预防和控制的最优策略.自1927年美国数学家Kermack和苏格兰医学家、流行病学家Mckendrick构造了著名的传染病仓室模型以来,数学模型成为研究疾病传播规律、评估感染风险、优化控制策略的重要工具,参见文献[4].

我们将钻石公主号邮轮上人群分为两类:健康人群和感染人群.新冠病毒肺炎在邮轮上传播满足以下假设:

(1)总人数恒定,即健康人群与感染人群之和为常数$N$,这里$N=3711$为邮轮总人数;

(2)不考虑死亡和治疗情况;

我们建立一个简单的$SI$仓室数学模型,变量$S(t)$表示$t$时刻健康人群数量, $I(t)$表示$t$时刻感染人群数量,健康人群和感染人群数量变化满足下面方程:

(2.1) $\begin{eqnarray}S'(t)=-\beta \frac{S(t)}{N}I(t), \end{eqnarray}$

(2.2) $ I'(t)=\beta \frac{S(t)}{N}I(t), $

这里,参数$\beta$表示接触传播率且满足$\beta\geqslant0$.邮轮上最初感染者假定为一人,故模型(2.1)-(2.2)初始条件为:

$ S(0)=3710, \quad \quad \quad I(0)=1. $

由上面假设知, $S(t)+I(t)=N$,于是$S(t)=N-I(t)$,代入方程(2.2)得

(2.3) $\begin{eqnarray}\label{3} I'(t)=\beta(1-\frac{I(t)}{N})I(t). \end{eqnarray}$

很显然,方程(2.3)为经典的Logistic增长模型.

通过求解方程(2.3),得到感染人群的解析表达式为

(2.4) $\begin{eqnarray}\label{4}I(t)=\frac{NI_0e^{\beta t}}{N+I_0(e^{\beta t}-1)}, \quad \quad I_0=I(0)=1.\end{eqnarray}$

容易看出:

(1)当病毒不具备传播条件时,即$\beta=0$,此时$I(t)\equiv 1$,意味着染病人数不会增加;

(2)当存在病毒持续传播时,即$\beta>0$,此时$\lim\limits_{t\rightarrow\infty}I(t)=N$.意味着随着时间发展,最终所有人染病.具体感染人数$I(t)$随时间的发展曲线可参见图 2.

下面利用日本政府于2020年2月1日至2020年2月18日公布的钻石公主号邮轮感染人数信息,参见文献[3] (见表 1),结合感染函数(2.4),利用最小二乘法估算感染率$\beta$的值,参见文献[5],方法如下:

所选择的回归模型应该使所有观察值的残差平方和达到最小.样本回归模型为

$ \begin{eqnarray} I_i=\frac{NI_0e^{\beta t_i}}{N+I_0(e^{\beta t_i}-1)}+e_i\Rightarrow e_i=I_i-\frac{NI_0e^{\beta t_i}}{N+I_0(e^{\beta t_i}-1)}, \end{eqnarray} $

其中$e_i$为样本$(t_i, I_i)$的误差.平方损失函数为

$ \begin{eqnarray} Q=\sum\limits_{i=1}^{n}e_i^2=\sum\limits_{i=1}^{n}\left(I_i-\frac{NI_0e^{\beta t_i}}{N+I_0(e^{\beta t_i}-1)}\right)^2. \end{eqnarray} $

Q为残差平方和,通过$Q$最小确定函数,即确定$\beta$,把$\beta$看作$Q$的函数,变成求极值的问题,可以通过求导数得到.求$Q$对待估参数的偏导数为

$ \begin{eqnarray} \frac{\partial Q}{\partial \beta}=2\sum\limits_{i=1}^{n}\left(\frac{NI_0e^{\beta t_i}}{N+I_0(e^{\beta t_i}-1)}-I_i\right)\frac{\beta N(N-1)e^{\beta t_i}}{(N-1+e^{\beta t_i})^2}, \end{eqnarray} $

令偏导数为0,利用Matlab软件,得到$\beta=1.1177$,其95%的置信区间为(1.0846, 1.1507).

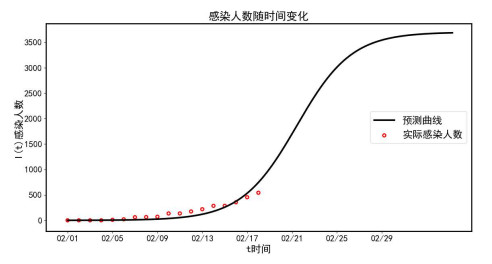
应用上述参数$\beta$的估计值和方程(2.4), 图 1刻画了疫情在钻石公主号邮轮上的发展趋势曲线,其中官方公布的确诊人数用红色圆圈标记.从图 1可以看出,曲线很好吻合了2020年2月1日至2020年2月18日的疫情发展,可以预测在不进一步采取措施情况下,邮轮上染病人数将会爆发,三月中旬会感染全体船上人员,无一幸免.

进一步地,我们假设对钻石公主号邮轮上的染病人群采取完全的隔离措施,引入参数$\theta$表示隔离效果,这里$0 <\theta <1$.得到如下考虑对染病者采取有隔离措施的SI模型:

(3.1) $S'(t)=-(1-\theta)\beta \frac{S(t)}{N}I(t), $

(3.2) $I'(t)=(1-\theta)\beta \frac{S(t)}{N}I(t). $

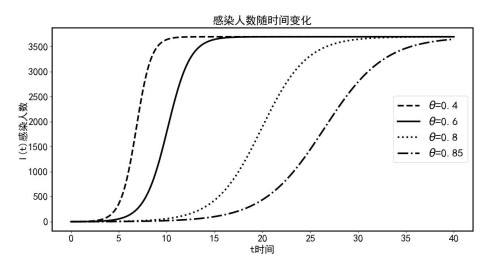
下面我们对参数$\theta(0 <\theta <1)$选取不同的数值刻画隔离效果, $\theta$值越大,表示隔离越彻底. 图 2刻画了在不同隔离效果下新冠肺炎染病人数的动态发展曲线.隔离措施越好,接触率越低,越能延缓疾病传播和发展,表明对染病者和潜伏者采取及时的隔离,是完全有效的防控措施.

我们建立了一个简单的数学模型,对日本钻石公主号邮轮上新型冠状病毒肺炎的传播进行刻画.通过数学分析和数值仿真,我们发现在封闭空间中新冠肺炎流行病的发展趋势.针对新型冠状病毒(SARS-Cov-2)高传染性,我们给出以下结论和疫情防控措施建议,这些结论和建议可同样适用于其他封闭空间的传播环境,如采取封校措施的大学校园、监狱、封闭的机舱以及城市中的楼栋等等.

(1)从模型分析及数值拟合可以看出,在封闭环境下,不考虑治疗和隔离的措施,传染会无限制扩大,最终无一幸免,所有人将会全部感染病毒.

(2)从钻石公主号邮轮的感染数据及模型预测看出,即使邮轮采取部分隔离,而不是完全地隔离,因为病毒会通过空气流通,空调系统,下水道等传播,这些措施从模型角度看只能减小接触率$\beta$,但只要存在与病毒的接触,即$\beta>0$,从解析表达式(2.4)可以看出,传染不会终止.

(3)从图 1可以看出,新冠肺炎传播早期一段时间发展缓慢,中后期会指数爆发增长.意味着流行病在传播早期是一段关键的可控窗口期,此时需要简单快捷的筛查方法尽快查出染病患者并进行隔离.能在窗口期控制住病毒的扩散,是战胜疫情爆发的关键.

(4)在封闭空间中,人群的密度高,接触率难以减小,这种环境不利于对健康人群的保护,会促成疾病爆发.在感染早期,人群的分散可以减少接触率,减缓传播.可以采取的措施为:对于健康人群,通过分散降低人口密度,降低接触率;对于感染人群,要早发现,早隔离,早治疗.