1 模型
1.1 研究背景
在传染病动力学中,基本再生数是一个很重要的概念,其表示单个感染者在完全易感染人群中生成的第二代期望数,被用来衡量疾病的传染能力大小,可以作为判断疾病在种群中流行与消亡的阈值[5]. Liang和Zhao等[6-7]中引入了带有时滞的周期传染病模型基本再生数的定义方法,并证明了基本再生数与染病者变量在周期无病平衡点处线性化方程对应Poincáre映射谱半径在刻画疾病传播的"阈值"作用方面的等价性,是针对周期性传染病模型(包括具有阶段特征的种群演化周期模型)动力学研究的突破性成果.自此之后, Bai[8]和Lou[9]等以此为理论基础,分别研究了一类周期疟疾模型和一个寄生虫的演化模型,更多的相关研究可以参阅文献[11-12].特别指出,作为应用, Zhao等在文献[7]中研究了一个带有离散时滞的SEIR常微分方程传染病模型,定义了模型的基本再生数,并证明了基本再生数在决定疾病是否一致持久的"阈值"作用.
1.2 模型
文献[7]所考虑的时间周期时滞常微分方程模型如下:
其中,
(H1)
(H2)
(ⅰ)
(ⅱ)对所有的
为了得到带有周期性潜伏期的SEIR模型,本文假定潜伏期是一个与时间有关的严格为正的周期函数
引入染病年龄分布函数
其中
令
对
和
注 根据生态学、传染病学意义[9],
由于任何个体的生命都是有限的,因此
求解以上方程,得到
则
从而得到如下带有周期性潜伏期的SEIR传染病模型
注意到
为了使系统(1.2)的解是连续的[10],本文始终假定系统(1.2)中初值条件满足
由初值条件(1.3)知
这意味着系统(1.2)中
为了简化问题,将第二个方程从系统(1.2)中去掉,考虑如下系统即可
本文将借助于耗散动力系统的相关理论结合时滞周期系统基本再生数理论研究系统(1.5) (系统(1.2))的动力学.周期性潜伏期
2 基本再生数
2.1 解的存在唯一性
令
显然,对于任意满足(1.3)的
由于
有唯一的全局吸引的周期解
由比较原理知对于任意满足条件(1.3)的
引理2.1 对于任意
引理2.2 对于任意
证 令
即
从而得到以下微分方程
对于给定
即
从而得到以上方程的解
2.2 基本再生数
将系统(1.5)在
这里
令
定义次代算子
令
紧接着,定义算子
对任意
对任意
引理2.3
3 阈值动力学
引理3.1 令
证 令
即
从而
由于
因此,
令
定理3.1 假定H1成立,有如下结论成立:
(ⅰ)如果
(ⅱ)如果
证 (ⅰ)当
这里
另一方面,由于方程(2.1)有唯一的全局吸引的周期解
这里
存在充分大的常数
(ⅱ)当
对于任意
这里
令
论断
采用反证法,假设存在
从而存在
由(3.3)式知只要
此时,
这里
令
由(3.5)式和比较原理得
因此,
且初值为
由以上论断知:
为了证明实际持久性,采用类似于文献[17,定理4.1]的方法.定义一个连续函数
由
此外,由系统(1.5)中关于
则
根据定理3.1,当
亦是
定理3.2 假定H1成立,有如下结论:
(ⅰ)如果
(ⅱ)如果
4 数值模拟
本节将利用数值方法模拟、验证上节结论,并分析忽略潜伏期的周期性而取其平均值对估计疾病传播能力的造成的误差和影响.由于系统(1.5)是非自治的,无法得到基本再生数的精确值,因此采用文献[18]中提出的针对周期系统基本再生数的数值计算方法近似计算基本再生数
首先,令
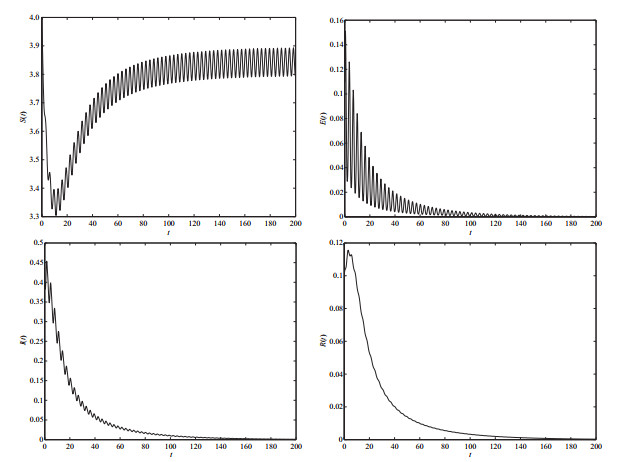
图 1
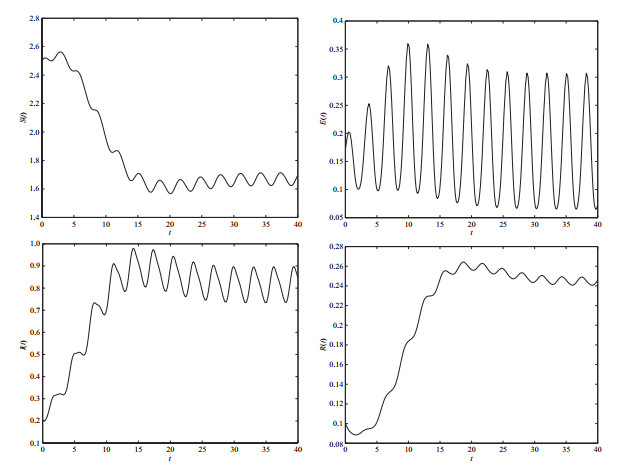
图 2
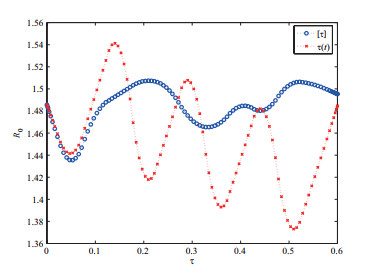
其次,借助数值方法检验忽略潜伏期的周期性对估计疾病传播能力的影响.固定
现分别计算
图 3
5 结语
本文利用动力系统的理论和方法研究了一类具有周期性潜伏期的SEIR传染病模型,得到了阈值动力学结果:当
参考文献
仓室传染病模型基本再生数的发展简介
Basic repoduction numbers for compartmetal epidemic models
Basic reproduction ratios for periodic abstract functional differential equations (with application to a spatial model for Lyme disease)
DOI:10.1007/s10884-017-9601-7 [本文引用: 2]
Basic reproduction ratios for periodic compartmental models with time delay
DOI:10.1007/s10884-015-9425-2 [本文引用: 8]
A reaction-diffusion malaria model with seasonality and incubation period
DOI:10.1007/s00285-017-1193-7 [本文引用: 1]
A theoretical aproach to understanding population dynamics with seasonal developmental durations
DOI:10.1007/s00332-016-9344-3 [本文引用: 4]
Threshold dynamics of a time periodic reaction-diffusion epidemic model with latent period
DOI:10.1016/j.jde.2014.12.032 [本文引用: 1]
一类具时滞的周期logistic传染病模型空间动力学研究
Spatial dynamics of periodic reaction-diffusion epidemic models with delay and logistic growth
Understanding the link between malaria risk and climate
DOI:10.1073/pnas.0903423106 [本文引用: 1]
一类时间周期的时滞反应扩散模型的空间动力学研究
Spatial dynamics of a class of delayed nonlocal reaction-diffusion models with a time period
Global attractors and steady states for uniformly persistent dynamical systems
DOI:10.1137/S0036141003439173 [本文引用: 1]
Threshold dynamics in a time-delayed periodic SIS epidemic model