1 引言
考虑半参数部分非线性变系数模型
其中
就作者所知,目前将响应变量缺失,协变量带测量误差这一复杂数据情况应用到部分非线性变系数模型的结果还较少.然而在实际问题中,经常会遇到数据缺失现象,缺失数据的处理一直受到统计学家的重视.另外,在多数情况下很可能得不到协变量的准确观测值,只能得到含有误差的观测值.也就是说变量带测量误差的模型在响应变量缺失下的研究是很有必要的,带测量误差的模型统称为EV模型.针对缺失数据, Zhou等[4]研究了一类存在缺失数据时的借补估计方程方法,这些方法可以用到部分线性及非线性模型中来; Xue和Li[5]构造了响应变量有缺失数据的填补估计,证明了估计量的渐近性质,并在响应变量缺失下构造了线性模型中参数的经验似然置信域.针对测量误差数据, Carroll和Ruppert[6]详细讨论了非线性EV模型;冯三营等[7]研究了未知系数函数的经验似然问题,利用纠偏方法得到了似然比统计量,并给出了相关的性质、证明及模拟.针对缺失数据和测量误差数据同时存在的情况, Liang等[8]讨论了协变量含测量误差和响应变量存在缺失时的部分线性模型的统计推断问题; Wei[9]针对部分线性变系数模型研究了响应变量缺失和协变量带有测量误差情况下的估计问题.基于以上原因,本文研究响应变量缺失且协变量带有测量误差情况下的半参数部分非线性变系数模型的统计推断问题,采用局部线性回归技术(详见文献[10])来估计非参数函数分量
2 估计方法与主要结果
假设
其中
其中
模型(2.3)可以看成是传统的变系数模型.所以可以利用局部线性方法估计变系数函数
其中
且
极小化
由于
于是当给定
其中
可得到
其中
步骤1 给定初始估计
步骤2 由
步骤3 令
考虑真实参数
C1:随机变量
C2:
C3:存在正数
C4:非参数函数
C5:核权函数
C6:当
C7:对任何
C8:
C9:矩阵
C10:选择概率
注2.1 条件C1, C3–C4, C7–C8是常用于部分线性变系数模型和非线性函数中的条件.条件
定理2.1 在条件
其中
定理2.2 在条件
其中
下面给出选择概率未知时估计的大样本性质.为减少“维数灾祸”现象的影响,本文考虑用
定理2.3 设条件
定理2.4 设条件
3 模拟研究
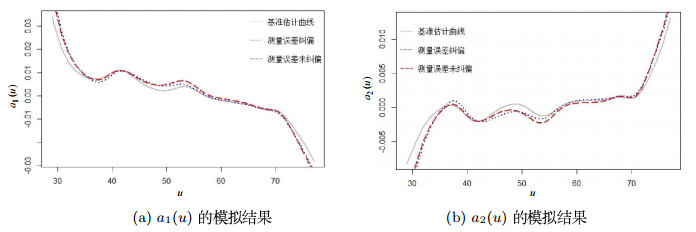
我们通过数值模拟来验证上一节提出的估计方法,基于模型
模拟中选取高斯核函数
表 1 基于完全情况数据下参数\beta的估计结果
| \sigma_e^{2} = 0.1^{2} | \sigma_e^{2} = 0.5^{2} | ||||||
| n | \beta | Bias | SD | MSE | Bias | SD | MSE |
| 100 | \hat{\beta}_1 | -0.0016 | 0.0114 | 1.334e-04 | -0.0170 | 0.1045 | 0.0112 |
| \hat{\beta}_2 | 0.0008 | 0.0146 | 2.148e-04 | 0.0141 | 0.1053 | 0.0113 | |
| 200 | \hat{\beta}_1 | 0.0001 | 0.0050 | 2.546e-05 | -0.0005 | 0.0051 | 2.697e-05 |
| \hat{\beta}_2 | -0.0004 | 0.0066 | 4.418e-05 | -0.0008 | 0.0081 | 6.685e-05 | |
| 400 | \hat{\beta}_1 | -0.0001 | 0.0022 | 4.916e-06 | -0.0004 | 0.0026 | 6.698e-06 |
| \hat{\beta}_2 | -0.0001 | 0.0027 | 7.188e-06 | -0.0001 | 0.0025 | 6.395e-06 |
表 2中将利用逆概率加权局部纠偏法得到的估计记为
表 2 基于逆概率加权法考虑测量误差和忽略测量误差情况下得到的参数估计的表现
| \hat{\beta}^{HT} | \hat{\beta}^{NE} | |||||||
| \beta | \sigma_e^{2} | n | Bias | SD | MSE | Bias | SD | MSE |
| \beta_1 | 0.1^{2} | 100 | -0.0013 | 0.0091 | 8.558e-05 | 0.0105 | 0.0142 | 3.112e-04 |
| 200 | -0.0007 | 0.0045 | 2.117e-05 | 0.0068 | 0.0057 | 7.865e-05 | ||
| 400 | 0.0003 | 0.0016 | 2.614e-06 | -0.0008 | 0.0027 | 8.244e-06 | ||
| 0.5^{2} | 100 | 0.0019 | 0.0093 | 9.010e-05 | 0.0114 | 0.0147 | 3.461e-04 | |
| 200 | -0.0008 | 0.0052 | 2.843e-05 | 0.0062 | 0.0065 | 8.049e-05 | ||
| 400 | 0.0002 | 0.0018 | 3.443e-06 | 0.0048 | 0.0051 | 4.916e-05 | ||
| \beta_2 | 0.1^{2} | 100 | 0.0001 | 0.0116 | 1.345e-04 | 0.0022 | 0.0155 | 2.451e-04 |
| 200 | 0.0003 | 0.0065 | 4.240e-05 | -0.0009 | 0.0071 | 5.114e-05 | ||
| 400 | -0.0004 | 0.0019 | 3.881e-06 | 0.0003 | 0.0039 | 1.557e-05 | ||
| 0.5^{2} | 100 | -0.0016 | 0.0138 | 1.930e-04 | 0.0026 | 0.0274 | 7.575e-04 | |
| 200 | -0.0007 | 0.0065 | 4.382e-05 | 0.0014 | 0.0112 | 1.271e-04 | ||
| 400 | -0.0001 | 0.0026 | 7.035e-06 | 0.0004 | 0.0048 | 2.353e-05 |
图 1
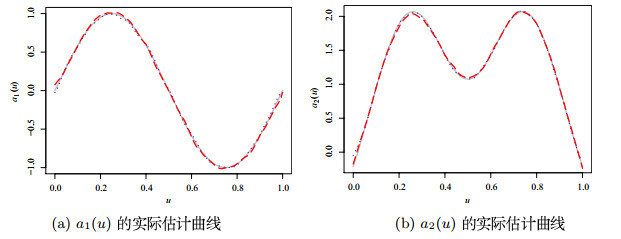
4 实例分析
这里选取一个心脏病数据来验证提出的方法在实际中的可用性.在此次实际数据分析中选取最大心率作为响应变量(
图 2
5 定理的证明
引理5.1 设
证 证明详见文献[13].
引理5.2 设
证 证明详见文献[14].
引理5.3 在条件
证 证明详见文献[15].
引理5.4 设
证 由于三式的证明类似,所以这里仅给出(5.3)式的证明.简单计算可得
利用引理5.1,条件期望的平滑性并结合文献[11,定理2]的证明过程,易证(5.3)式成立.
引理5.5 在条件
其中
证 结合引理(5.1)–(5.3)并利用大数定律,类似Li和Mei[16]可证(5.6)式成立.下证(5.7)式.利用引理5.1,引理5.3和引理5.4简单计算可得
引理5.5证毕.
引理5.6 设C1, C5, C6, C10条件成立,则当
证 根据引理
结合条件
引理5.6证毕.
引理5.7 在条件
证 结合引理
引理5.8 在条件
证 结合与引理
引理5.9 在条件
证 结合条件C3, C5,引理
引理5.10 设
证 将(5.12)式拆解成2项,简单计算可得
下面对
下证
因此,根据引理5.2、5.6,条件C3、C7、C8有
同理设
类似计算
下证
类似计算
类似方法将(5.13)式拆解为4项,即
接着将
下面证明
取上面矩阵中的任意一个元素来分析,由条件C2–C8知
类似可以计算
下面证明
类似可以计算
引理5.10得证.
定理2.1的证明 结合
其中
记
再结合引理5.5和条件C7, C8,由于
由于
其中
根据Slutsky定理有
定理2.2的证明 由
首先考虑
将上式代入
最后考虑
其次计算
记
然后计算
利用Slutsky整理可得
其中
定理2.2得证.
定理2.3和定理2.4的证明 应用定理2.1和2.2和引理5.3–5.10可以将缺失概率未知时参数
然后根据Slutsky定理,便可证明定理2.3和定理2.4.此处不再做详细证明过程.
参考文献
Statistical methods with varying coefficient models
DOI:10.4310/SII.2008.v1.n1.a15 [本文引用: 1]
Efficient statistical inference procedures for partially nonlinear models and their applications
DOI:10.1111/j.1541-0420.2007.00937.x [本文引用: 1]
Estimating equations inference with missing data
DOI:10.1198/016214508000000535 [本文引用: 1]
Empirical likelihood for linear models with missing responses
DOI:10.1016/j.jmva.2008.12.009 [本文引用: 1]
Measurement error in nonlinear models
部分线性变系数EV模型估计的渐近正态性
DOI:10.3969/j.issn.1672-6871.2011.02.021 [本文引用: 3]
Asymptotic normality of estimators for partially linear varying coefficient errors-in-variables Models
DOI:10.3969/j.issn.1672-6871.2011.02.021 [本文引用: 3]
Partially linear models with missing response variables and error-prone covariates
Estimation in varying-coefficient errors-in-variables models with missing response variables
DOI:10.1080/03610918.2010.542846 [本文引用: 1]
Corrected local polynomial estimation in varying-coefficient models with measurement errors
DOI:10.1002/cjs.5550340303 [本文引用: 3]
Statistical inference for a varying-coefficient partially nonlinear model with measurement errors
DOI:10.1016/j.stamet.2016.05.004 [本文引用: 1]
Weak and strong uniform consistency of kernel regression estimates
DOI:10.1007/BF00539840 [本文引用: 1]
Empirical likelihood for partially linear models
DOI:10.1006/jmva.1999.1866 [本文引用: 1]
协变量随机缺失下的广义半参数模型
The generalized semiparatric models with missing covariates
Estimation and inference for varying coefficient partially nonlinear models
DOI:10.1016/j.jspi.2013.05.011 [本文引用: 1]
Profile likelihood inferences on semiparametric varying-coefficient partially linear models
Statistical inference for semiparametric varying-coefficient partially linear models with error-prone linear covariates