分数阶微积分的理论距今已有$ 300 $多年的历史,它是在整数阶微积分理论上推广而来的,是关于任意阶导数和积分的理论,与整数阶微积分一样有着举足轻重的地位.起初分数阶导数有许多定义,但并不能证明定义间是互相等价的,不免使其前期发展较为缓慢.随着科技的不断发展以及专家学者们不断地探索钻研,发现在实际生活中有很多复杂现象很难用整数阶微积分理论进行刻画,而分数阶导数具有的全局相关性可以很好地描述具有记忆和遗传特性的材料和过程,并且可以克服整数阶微分理论与实验结果吻合不好的严重缺点,因此分数阶微分方程得到了广泛的关注并有许多学者对其进行了深入的研究.

研究发现包含分数阶微分算子的微分方程作为描述物理、力学、化学、工程等领域问题的建模工具是行之有效的,因此被广泛地应用于信号处理、控制工程、电磁学、电化学、生物科学、流体力学、扩散过程、连续统计学和统计力学,黏弹性材料动力学等.但是由于分数阶导数具有历史依赖性,使得计算分数阶微分方程的解析解相当复杂且困难,而给出数值算法求得其近似解显得格外必要.其中已经有许多有效的求解方法,如文献[1-2]运用算子矩阵法分别求解了分数阶奇异Volterra积分微分方程和线性分数阶微分方程两点及多点边值问题.文献[3]介绍了离散样条法求解两点分数阶Bagley-Torvik方程并给出了相应的收敛性分析.文献[4]将光滑变换法与样条配置法相结合求解了非线性分数阶初边值问题.文献[5]中Karaaslan等人用杂交不连续的加勒金法求解了分数阶初边值问题.文献[6-7]介绍了同伦分析法求解分数阶微分方程初边值问题;文献[8]研究了Adomian分解法求解高阶分数阶微分方程,并说明了该方法不仅可以求解线性的,求解非线性仍具有很好的效果;文献[9]给出了同伦扰动法求解分数阶微分方程组,并表明该方法在大多数情况下,只需要几次迭代就可获得快速收敛的级数解.文献[10]运用变分迭代法研究了分数阶微分方程.文献[11]与文献[12]均介绍了微分变换法,但文献[11]以广义的泰勒公式为基础避免了文献[12]中的误差,所得结果更为精确.文献[13]将外激励法与向后替代法相结合研究了分数阶微分方程特征值问题,其数值结果也表明了该方法具有较高的精度,可以有效的解决一类特征值问题.文献[14]提出用一种隐式无条件的稳定差分格式求解了一类线性空间-时间分数阶对流扩散方程.文献[15]提出了一种新的有限差分预估校正方法求解了非线性分数阶微分方程,同时该方法也可以进一步扩展到求解分数阶微分方程组.文献[16]运用配置法研究了带有非奇异Mittag-Leffler核的分数阶微分方程组的解以及其解的存在性以及规律性,同时也给出了相应的数值算例表明了该方法的有效性.文献[17]介绍了一种新的方法,即将Sumudu变换法与局部分数阶导数意义下的Adomian分解法相结合,该方法可用于描述不可微分的问题,并且非常有效的求解了线性非局部分数阶偏微分方程.文献[18]将$ p $阶块边值法与$ m $阶Lagrange插值相结合得到了一种新的数值方法,应用该方法求解了Caputo导数意义下的非线性分数阶微分方程,并证明了该方法的收敛性以及全局稳定性.文献[19]将经典的Legendre小波进行了推广,定义了一种新的分数阶小波基,推导出了该分数阶小波在Caputo意义下的导数和分数阶导数的算子矩阵.然后提出了一种基于这些算子矩阵和经典的$ Tau $方法的数值格式高效的求解了分数阶微分方程.

近年来,再生核理论得到了越来越广泛的应用,如在文献[20]基于再生核Hilbert空间给出了一维的Swift-Hohenberg方程的数值解法.文献[21]提出了一种结合有限差分法和拟牛顿法的高效再生核方法研究了Allen-Cahn方程,其数值算例表明新的再生核方法是具有高精度的,并且在完全离散的情况下仍然可以保持能量定律.文献[22]利用了简化的再生核方法求解了具有变系数的线性Volterra积分方程,避免了耗时的施密特正交化过程,同时证明了数值解是均匀收敛的,而且首次分析了近似解的收敛阶和稳定性,等等.再生核理论不仅可以很好地求解上述问题,而且在求解分数阶微分方程方面也是非常有效的.其中文献[23]运用了再生核方法求解了变分数阶函数边值问题并给出了相应的误差估计;文献[24]以再生核理论为基础结合样条函数提出了具有高精度且高效的数值方法;文献[25]研究了再生核方法求解非局部分数阶边值问题,使得再生核理论得到了更广泛的应用;文献[26-28]均以再生核理论为基础提出了更为有效的方法进行求解.

因此,该文以再生核理论为基础结合Legendre多项式得到了一种新的求解分数阶微分方程的数值算法,该方法构造了一个新的再生核空间,并给出了该空间下的多项式形式的再生核函数,其避免了经典再生核函数的分段式,使得在计算过程中可节约大量时间,所得结果更为精确有效.

此文主要研究以下形式的分数阶微分方程边值问题

(1.1) $ \begin{equation} \left\{ \begin{array}{lr} a(x)D^{\alpha}u(x)+b(x)u''(x)+c(x)u'(x)+d(x)u(x) = f(x), \\ u(0) = \lambda_{1}, u(1) = \lambda_{2}, \\ \end{array} \right. \end{equation} $

其中$ 1<\alpha<2, \; \lambda_{1}, \lambda_{2} $为常数, $ a(x), b(x), c(x), d(x)\in C^{2}[0, 1] $, $ u(x), f(x)\in C[0, 1] $, $ D^{\alpha} $为Caputo型分数阶导数.

文章由以下几部分组成:第二节给出了一些基本概念和定义;第三节介绍了移位Legendre多项式的定义、递推公式及其解析形式;第四节给出了运用再生核-移位勒让德基函数法求解的具体过程;第五节和第六节分别给出了所提方法的误差估计及收敛性分析;最后,数值算例表明了该方法的有效性.

定义2.1   Caputo型分数阶导数$ D^{\alpha} $定义为

(2.1) $ \begin{equation} ^{C}_{a}D_{x}^{\alpha}u(x) = \frac{1}{\Gamma(n-\alpha)}\int_{a}^{x}\frac{1}{(x-\tau)^{\alpha-n+1}}(\frac{{\rm d}^{n}}{{\rm d}\tau^{n}}u(\tau)){\rm d}\tau, \end{equation} $

其中$ C $为Caputo的缩写, $ \alpha $为阶数, $ \alpha\in R_{+}, \; n-1<\alpha<n, \; n\in N_{+} $.

定义2.2  若$ Q_{n}: = Span\{H_{0}(x), H_{1}(x), \cdots, H_{n}(x)\} $是一个内积空间,则该空间下的内积和范数为

(2.2) $ \begin{equation} \langle u(y), v(y)\rangle = \int_{0}^{1}w(y) u(y) v(y){\rm d}y \end{equation} $

和

(2.3) $ \begin{equation} \parallel u \parallel = \sqrt{\langle u, u\rangle}, \end{equation} $

其中$ w(y) $表示权函数.

定义2.3  若任意的序列$ h_{0}, h_{1}, h_{2}, \cdots $关于权函数$ w(x) $是正交的,则有$ \langle h_{i}, h_{j}\rangle = 0 $,其中$ i\neq j $.

当区间为$ [-1, 1], $权函数$ w(x) $ = 1时,将$ \{1, x, x^2, \cdots , x^n, \cdots \} $做正交化处理得到的多项式称为Legendre多项式,记为$ \{P_{n}(x)\}_{n = 0}^{\infty} $.

由于该文要在$ [0, 1] $区间上讨论,故作变换$ x = 2t-1 $,则有$ P_{n}(x) = P_{n}(2t-1) $,将其称为移位Legendre多项式,记$ L_{n}(t) = P_{n}(2t-1). $

显然$ \{L_{n}(t)\}_{n = 0}^{\infty} $在区间[0, 1]上关于权函数$ w(t) = 1 $正交,即

(3.1) $ \begin{equation} \int_{0}^{1}L_{n}(t)L_{m}(t){\rm d}t = \frac{1}{2n+1} \delta_{nm}, \end{equation} $

并且$ L_{i}(t) $有如下的递推关系式

(3.2) $ \begin{equation} L_{i+1}(t) = \frac{(2i+1)(2t-1)}{i+1}L_{i}(t)-\frac{i}{i+1}L_{i-1}(t), \; \; i = 1, 2, \cdots , \end{equation} $

其中$ L_{0}(t) = 1, L_{1}(t) = 2t-1 $.

下面给出$ n $阶移位Legendre多项式的解析形式(其中将变量$ t $变为$ x $)

(3.3) $ \begin{eqnarray} L_{n}(x) & = &(-1)^n\sum\limits_{k = 0}^{n}C_{n}^{k}C_{n+k}^{k}(-x)^k {}\\ & = &(-1)^n\sum\limits_{k = 0}^{n}\frac{n!}{k!(n-k)!}\frac{(n+k)!}{k!n!}(-1)^k x^k{}\\ & = &(-1)^{n+k}\sum\limits_{k = 0}^{n}\frac{(n+k)!}{(n-k)!(k!)^2}. \end{eqnarray} $

定理4.1  移位Legendre多项式$ \{L_{0}(x), L_{1}(x), \cdots, L_{n}(x)\} $是$ {\mathbb R}^{n} $空间中的一组基函数.

证  设存在不全为零的数$ a_{0}, a_{1}, \cdots , a_{n} $,使得

(4.1) $ \begin{equation} a_{0}L_{0}(x)+a_{1}L_{1}(x)+\cdots+a_{n}L_{n}(x) = 0. \end{equation} $

在方程左右两边分别与$ L_{i}(x) $做内积,可得

(4.2) $ \begin{equation} \begin{array}{ll} \langle L_{i}(x), a_{0}L_{0}(x)+a_{1}L_{1}(x)+\cdots+a_{n}L_{n}(x)\rangle = 0, \\ \langle L_{i}(x), a_{0}L_{0}(x)\rangle + \langle L_{i}(x), a_{1}L_{1}(x) \rangle +\cdots+\langle L_{i}(x), a_{n}L_{n}(x)\rangle = 0. \end{array} \end{equation} $

由移位Legendre多项式关于权函数$ w(x) = 1 $正交的性质,当取$ w(x) = 1 $时,有

(4.3) $ \begin{equation} \langle L_{i}(x), L_{j}(x)\rangle = 0 , \; \; \; i\neq j. \end{equation} $

因此,可整理得

(4.4) $ \begin{equation} a_{i}\langle L_{i}(x), L_{i}(x)\rangle = 0. \end{equation} $

进而有$ a_{i} = 0 (i = 0, 1, 2, \cdots , n) $.所以$ \{L_{0}(x), L_{1}(x), \cdots, L_{n}(x)\} $是线性无关的.令

(4.5) $ \begin{equation} \left\{ \begin{array}{lr} H_{0}(x) = 1, \\ { } H_{k}(x) = L_{k}(x)+\sum\limits_{j = 0}^{k-1}C_{kj}H_{j}(x), \; (k = 1, 2, \cdots , n), \\ \end{array} \right. \end{equation} $

其中

(4.6) $ \begin{equation} C_{kj} = -\frac{\langle L_{k}(x), H_{j}(x)\rangle}{\langle H_{j}(x), H_{j}(x)\rangle}, {\quad} j = 0, 1, \cdots , k-1. \end{equation} $

则可得任意的$ H_{i}(x)\in {{\Bbb R}}^{n} (i = 0, 1, \cdots , n) $都可由$ \{L_{0}(x), L_{1}(x), \cdots, L_{n}(x)\} $线性表示.综上所述,移位Legendre多项式$ \{L_{0}(x), L_{1}(x), \cdots, L_{n}(x)\} $可以做成空间$ {\mathbb R}^{n} $的一组基,并且$ \{H_{0}(x), H_{1}(x), \cdots, H_{n}(x)\} $是以$ w(x) (w(x)\neq 1) $为权函数的正交多项式组.

定理4.2  若$ Q_{n}: = Span\{H_{0}(x), H_{1}(x), \cdots, H_{n}(x)\} $,则$ \{H_{i}(x)\}_{i = 0}^{n} $是$ Q_{n} $中的一组正交基.

证  由定理4.1知,对$ \forall\; H_{i}(x), H_{j}(x) $,有$ \langle H_{i}(x), H_{j}(x)\rangle = 0\ (i\neq j) $,即满足正交性.所以下面只需证明$ \{H_{i}(x)\}_{i = 0}^{n} $可以做成一组基.

设存在不全为零的数$ d_{0}, d_{1}, \cdots, d_{n} $,使得

(4.7) $ \begin{equation} d_{0}H_{0}(x)+d_{1}H_{1}(x)+\cdots+d_{n}H_{n}(x) = 0. \end{equation} $

(4.7)式两边与$ H_{j}(x) $做内积,有

(4.8) $ \begin{equation} \langle H_{j}(x), d_{0}H_{0}(x)+d_{1}H_{1}(x)+\cdots+d_{n}H_{n}(x)\rangle = 0, \end{equation} $

(4.9) $ \begin{equation} \langle H_{j}(x), d_{0}H_{0}(x)\rangle + \langle H_{j}(x), d_{1}H_{1}(x) \rangle +\cdots+\langle H_{j}(x), d_{n}H_{n}(x)\rangle = 0.\\ \end{equation} $

因为$ \{H_{0}(x), H_{1}(x), \cdots, H_{n}(x)\} $是正交多项式组,所以$ d_{j}\langle H_{j}(x), H_{j}(x) \rangle = 0 $.因此有$ d_{j} = 0\; \; (j = 0, 1, \cdots , n) $.所以$ \{H_{0}(x), H_{1}(x), \cdots, H_{n}(x)\} $是线性无关的.

接下来证明对任意的$ g(x)\in Q_{n} $,都有$ g(x) = \sum\limits_{j = 0}^{n} m_{j}H_{j}(x) $,其中$ m_{j}\ (j = 0, 1, \cdots , n) $是确定的常数.

对任意的$ g(x)\in Q_{n} $, $ g(x) $是次数不超过$ n $的多项式,因此一定存在确定的常数$ r_{i} $$ (i = 0, 1, \cdots , n) $,使得

(4.10) $ \begin{equation} g(x) = \sum\limits_{i = 0}^{n}r_{i}L_{i}(x), \end{equation} $

再由(4.5)式可得

(4.11) $ \begin{equation} L_{i}(x) = H_{i}(x)-\sum\limits_{j = 0}^{i-1}C_{ij}H_{j}(x), \; i = 1, 2, \cdots , n. \end{equation} $

将(4.11)式代入(4.10)式可得

(4.12) $ \begin{eqnarray} g(x) & = &\sum\limits_{i = 0}^{n}r_{i}(H_{i}(x)-\sum\limits_{j = 0}^{i-1}C_{ij}H_{j}(x)){}\\ & = &r_{0}H_{0}(x)+\sum\limits_{i = 1}^{n}r_{i}(H_{i}(x)-\sum\limits_{j = 0}^{i-1}C_{ij}H_{j}(x)){}\\ & = &(r_{0}-r_{1}C_{10}-r_{2}C_{20}-\cdots-r_{n}C_{n0})H_{0}(x)+(r_{1}-r_{2}C_{21}-\cdots-r_{n}C_{n1})H_{1}(x){}\\ &&+\cdots+r_{n}H_{n}(x). \end{eqnarray} $

令

(4.13) $ \begin{equation} \begin{array}{ll} m_{0} & = r_{0}-r_{1}C_{10}-r_{2}C_{20}-\cdots-r_{n}C_{n0}, \\ m_{1} & = r_{1}-r_{2}C_{21}-\cdots-r_{n}C_{n1}, \\ &\cdots \\ m_{n}& = r_{n}. \end{array} \end{equation} $

显然$ m_{0}, m_{1}, \cdots, m_{n} $均为确定的常数,因此有

(4.14) $ \begin{equation} g(x) = m_{0}H_{0}(x)+m_{1}H_{1}(x)+\cdots+m_{n}H_{n}(x), \end{equation} $

所以,对任意的$ g(x)\in Q_{n} $,都有

(4.15) $ \begin{equation} g(x) = \sum\limits_{j = 0}^{n}m_{j}H_{j}(x). \end{equation} $

综上所述，$ \{H_{i}(x)\}_{i = 0}^{n} $是空间$ Q_{n} $的一组正交基.

由定理4.2知, $ \{H_{i}(x)\}_{i = 0}^{n} $是空间$ Q_{n} $的一组正交基,那么对于空间$ Q_{n} $中的任意一个函数都可由这组正交基线性表示.而每一个空间的核函数一定是属于这个空间的,因此核函数也可由这组正交基线性表示.又再生核函数一定是满足再生性的,故也可进一步说明空间$ Q_{n} $是一个再生核空间,且核函数的具体表示形式由以下引理给出.

引理4.1^[30]   $ Q_{n} $是一个再生核空间,它的再生核为

(4.16) $ \begin{equation} R_{n}(x, y) = \sum\limits_{j = 0}^{n}h_{j}(x)h_{j}(y), \end{equation} $

其中$ h_{j}(x) = \frac{H_{j}(x)}{\parallel H_{j}(x)\parallel} $.

由引理4.1以及核函数的再生性可得,对任意的$ u(y)\in Q_{n} $,有

(4.17) $ \begin{equation} \langle u(y), R_{n}(x, y)\rangle = u(x). \end{equation} $

引理4.2^[30]  设$ \{x_{i}\}_{i = 1}^{n} $是$ [0, 1] $上的一组互异稠密点集,令$ \varphi_{i}(x) = R_{n}(x_{i}, x) $, $ \psi_{i}(x) = L^{*}\varphi_{i}(x) $,则$ \{\psi_{i}(x)\}_{i = 1}^{n}\mathop{ = }\limits^{\rm def} L_{s}R_{n}(x, s)|_{s = x_{i}}, \; i = 1, 2, \cdots , n $.

证

(4.18) $ \begin{eqnarray} \psi_{i}(x) & = &\langle \psi_{i}(\cdot), R_{n}(x, \cdot)\rangle_{Q_{n}}{}\\ & = &\langle L^{*}\varphi_{i}(\cdot), R_{n}(x, \cdot)\rangle{}\\ & = &\langle \varphi_{i}(\cdot), LR_{n}(x, \cdot)\rangle{}\\ & = &\langle R_{n}(x_{i}, \cdot), LR_{n}(x, \cdot)\rangle{}\\ & = &L_{s}R_{n}(x, s)|_{s = x_{i}}. \end{eqnarray} $

证毕.

为了求解方程(1.1),首先将方程(1.1)的边界条件齐次化,则将求解方程(1.1)转化为求解以下方程

(4.19) $ \begin{equation} \left\{ \begin{array}{lr} a(x)D^{\alpha}u(x)+b(x)u''(x)+c(x)u'(x)+d(x)u(x) = f(x), \\ u(0) = 0, u(1) = 0.\\ \end{array} \right. \end{equation} $

为此,先定义一个线性算子$ L $,对$ u(x)\in Q_{n} $,令

(4.20) $ \begin{equation} Lu(x) = a(x)D^{\alpha}u(x)+b(x)u''(x)+c(x)u'(x)+d(x)u(x), \end{equation} $

则在再生核空间$ Q_{n} $中,求解方程(4.19)等价于求解以下算子方程

(4.21) $ \begin{equation} Lu(x) = f(x). \end{equation} $

下面基于再生核理论,给出求解方程(4.21)的具体步骤.

在区间$ [0, 1] $上任意选取$ n $个节点$ \{x_{i}\}_{i = 1}^{n} $,由引理$ 4.2 $,有

(4.22) $ \begin{equation} \psi_{i}(x) = L_{s}R_{n}(x, s)|_{s = x_{i}}, i = 1, 2, \cdots , n, \end{equation} $

对$ \psi_{i}(x) $做Gram-Schmidt正交化,可得到空间$ Q_{n} $的一组规范正交基$ \{\overline{\psi}_{i}(x)\}_{i = 1}^{n} $:

(4.23) $ \begin{equation} \overline{\psi}_{i}(x) = \sum\limits_{k = 1}^{i}\beta_{ik}\psi_{k}(x), {\quad} \beta_{ii}>0, i = 1, 2, \cdots , n, \end{equation} $

则在空间$ Q_{n} $中,方程(4.21)的近似解可表示为

(4.24) $ \begin{equation} u_{n}(x) = \sum\limits_{i = 1}^{n}\langle u, \overline\psi_{i}\rangle\overline\psi_{i}. \end{equation} $

定理4.3  在同一个向量空间中的任意两组基是彼此等价的,故方程$ (1.1) $的近似解也可表示成如下形式

(4.25) $ \begin{equation} u_{n}(x) = u(0)+\frac{u'(0)}{1!}x+\frac{u''(0)}{2!}x^2+\cdots+\frac{u^{(n-1)}(0)}{(n-1)!}x^{n-1}+\frac{u^{(n)}(\eta)}{n!}x^{n}, \end{equation} $

其中$ 0<\eta<x , x\in(0, 1) $.

定理5.1  假设$ u(x) $是方程$ (4.21) $的精确解, $ u_{n}(x) $是$ u(x) $的近似解,其中权函数$ w(x) = x^m $,则存在$ M > 0, m>0 $,使得

(5.1) $ \begin{equation} \parallel u(x)-u_{n}(x)\parallel_{w}\leq M\cdot\frac{1}{n!\sqrt{2n+m+1}}. \end{equation} $

证  由泰勒公式可得

(5.2) $ \begin{eqnarray} u(x) & = &u(0)+\frac{u'(0)}{1!}x+\frac{u''(0)}{2!}x^2+\cdots+\frac{u^{(n-1)}(0)}{(n-1)!}x^{n-1}+\frac{u^{(n)}(\xi)}{n!}x^{n}{}\\ & = &\sum\limits_{i = 0}^{n-1}\frac{u^{(i)}(0)}{i!}x^{i}+\frac{u^{(n)}(\xi)}{n!}x^{n}, \end{eqnarray} $

其中$ 0<\xi<x , x\in(0, 1) $.

由于$ u(x)\in C[0, 1] $,则$ u^{(n)}(x)\in C[0, 1] $,因此必有$ \mid u^{(n)}(x)\mid \leq M $,又$ M > 0 $是已知常数,因而有

(5.3) $ \begin{equation} \mid u(x)-\sum\limits_{i = 0}^{n-1}\frac{u^{(i)}(0)}{i!}x^{i}\mid = \mid\frac{u^{(n)}(\xi)}{n!}x^{n}\mid \leq \frac{M}{n!}x^n. \end{equation} $

由(2.2)和(2.3)式,有

(5.4) $ \begin{eqnarray} \parallel u(x)-u_{n}(x)\parallel_{w}^{2} &\leq& \parallel u(x)-\sum\limits_{i = 0}^{n-1}\frac{u^{(i)}(0)}{i!}x^{i}\parallel_{w}^{2}{}\\ &\leq &\frac{M^2}{(n!)^2}\int_{0}^{1}x^{2n}w(x){\rm d}x{}\\ & = &\frac{M^2}{(n!)^2}\int_{0}^{1}x^{2n}x^m {\rm d}x{}\\ & = &\frac{M^2}{(n!)^2}\int_{0}^{1}x^{2n+m} {\rm d}x{}\\ & = &\frac{M^2}{(n!)^2(2n+m+1)}. \end{eqnarray} $

对上式两边同时开平方,可得

(5.5) $ \begin{equation} \parallel u(x)-u_{n}(x)\parallel_{w}\leq \frac{M}{n!\sqrt{2n+m+1}}. \end{equation} $

定理5.1证毕.

定理6.1  假设$ \parallel u(x)\parallel_{C} $ = $ \max\limits_{x\in[0, 1]}\mid u(x)\mid_{Q_{n}} $,那么$ \parallel D^{\alpha}u(x)\parallel_{C}\leq M_{1}\parallel u(x)\parallel_{Q_{n}} $,其中$ M_{1} $是常数.

证  假设$ R_{n}(x, y) $是$ Q_{n} $的再生核函数,那么由再生性可得

(6.1) $ \begin{equation} u(x) = \langle u(\cdot) , R_{n}(x, \cdot)\rangle. \end{equation} $

根据Cauchy-Schwarz不等式,有

(6.2) $ \begin{equation} \begin{array}[b]{ll} \mid D^{\alpha}u(x)\mid_{C} & = \mid u(\cdot) , D^{\alpha}R_{n}(x, \cdot)\mid\\ &\leq \parallel u(\cdot)\parallel \cdot\parallel D^{\alpha}R_{x}(\cdot) \parallel\\ &\leq M_{1}\parallel u(x)\parallel_{Q_{n}}. \end{array} \end{equation} $

因此, $ \parallel D^{\alpha}u(x)\parallel_{C}\leq M_{1}\parallel u(x)\parallel_{Q_{n}} $,其中$ M_{1} $是常数.

定理6.2  若$ u(x) $是方程$ (4.21) $的精确解, $ u_{n}(x) $是$ u(x) $的近似解,则$ u_{n}(x) $一致收敛于$ u(x) $,分数阶导数$ D^{\alpha}u_{n}(x) $一致收敛于$ D^{\alpha}u(x) $.

证  首先证明$ u_{n}(x) $一致收敛于$ u(x) $.令$ R_{n}(x, y) $是再生核空间$ Q_{n} $的再生核函数,那么有

(6.3) $ \begin{equation} \begin{array}[b]{ll} \parallel u(x)-u_{n}(x)\parallel & = \mid \langle u(\cdot)-u_{n}(\cdot), R_{n}(x, \cdot)\rangle\mid\\ &\leq\parallel u(\cdot)-u_{n}(\cdot)\parallel\cdot \parallel R_{n}(x, \cdot)\parallel\\ &\leq N\parallel u-u_{n}\parallel, \\ \end{array} \end{equation} $

其中$ N\geq\parallel R_{n}(x, \cdot)\parallel \geq 0 $.因此, $ u_{n}(x) $一致收敛于$ u(x) $.接下来证明$ D^{\alpha}u_{n}(x) $一致收敛于$ D^{\alpha}u(x) $.

(6.4) $ \begin{equation} \begin{array}[b]{ll} \mid D^{\alpha}u(x)-D^{\alpha}u_{n}(x)\mid & = \langle u(\cdot)-u_{n}(\cdot), D^{\alpha}R_{n}(x, \cdot)\rangle\\ &\leq\parallel u(\cdot)-u_{n}(\cdot)\parallel\cdot \parallel D^{\alpha}R_{n}(x, \cdot)\parallel\\ &\leq N_{1}\parallel u-u_{n}\parallel. \end{array} \end{equation} $

因为$ \parallel u-u_{n}\parallel\rightarrow 0 $,所以$ \mid D^{\alpha}u(x)-D^{\alpha}u_{n}(x)\mid\rightarrow 0 $.因此, $ D^{\alpha}u_{n}(x) $一致收敛于$ D^{\alpha}u(x) $.

例1^[5]  考虑如下的分数阶微分方程边值问题

(7.1) $ \begin{equation} \left\{ \begin{array}{lr} D^{\alpha}u(x)+u(x)+u''(x) = f(x), \\ u(0) = 1, u(1) = 3, \\ \end{array} \right. \end{equation} $

其中$ \alpha $分别取$ 1.1, 1.2, 1.5, 1.7, 1.9, $$ f(x) = \frac{\Gamma(4)}{\Gamma(4-\alpha)}x^{3-\alpha}+x^3+7x+1 $,其精确解$ u(x) = x^3+x+1 $.

取$ n = 5 , w(x) = x, x_{i} = \frac{i}{n}, i = 1, 2, \cdots , n-1 $,用文中的方法计算的绝对误差$ \mid u_{n}(x)-u(x)\mid $与文献[5]的比较结果见表 1.

例2^[5]  考虑如下的分数阶微分方程问题

(7.2) $ \begin{equation} \left\{ \begin{array}{lr} D^{\alpha}u(x)+u(x)+u''(x) = f(x), \\ u(0) = 0, u(1) = 1, \\ \end{array} \right. \end{equation} $

其中$ \alpha = \frac{3}{2}, f(x) = 2+4\sqrt{\frac{x}{\pi}}+x^2 $,其精确解$ u(x) = x^2 $.

取$ n = 6\; , \; 7 , w(x) = x, x_{i} = \frac{i}{n}, i = 1, 2, \cdots , n-1 $,用文中的方法计算在取不同节点数时各节点处的绝对误差$ \mid u_{n}(x)-u(x)\mid $见表 2,与文献[5]的绝对误差的比较结果见表 3.

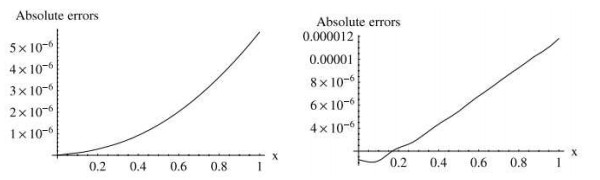
例3^[25]  考虑如下的分数阶微分方程问题

(7.3) $ \begin{equation} \left\{ \begin{array}{lr} D^{\alpha}u(x)+\cos(x)u'(x)+2u(x) = f(x), \\ u(0) = 0, u(1) = (1/8) + 2 u (1/2) + 31/49 u (7/8), \\ \end{array} \right. \end{equation} $

其中$ \alpha = 1.3, f(x) = 2x^2+2x\cos(x)+\frac{\Gamma(3)}{\Gamma(1.7)}x^{0.7} $,其精确解$ u(x) = x^2 $.

取$ n = 5, w(x) = x, x_{i} = \frac{i}{n}, i = 1, 2, \cdots , n-1 $,用文中的方法计算绝对误差$ \mid u_{5}(x)-u(x)\mid $以及$ \mid u_{5}'(x)-u'(x)\mid $,数值结果见图 1,文献[25]中的绝对误差$ \mid u_{10}(x)-u(x)\mid $以及$ \mid u_{10}'(x)-u'(x)\mid $见图 2.