再生核移位勒让德基函数法求解分数阶微分方程

摘要/Abstract

图/表 5

参考文献 30

Metrics

摘要：

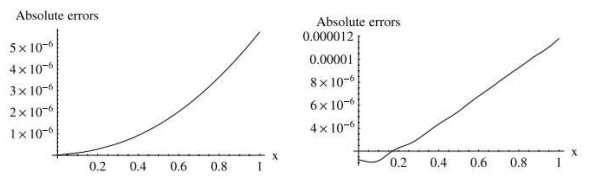
该文以再生核理论为基础，用移位Legendre多项式作为基函数构造了一个新的再生核空间，并给出了该空间下的再生核函数.与经典的再生核函数有所不同的是该空间下的再生核函数不再是分段函数，因此可以减小分数阶算子作用在核函数上时的计算量，使近似解更为精确.数值算例表明该方法的有效性.

关键词: 分数阶微分方程, 移位Legendre多项式, 再生核方法

Abstract:

Based on the theory of the reproducing kernel, this paper constructed a new reproducing kernel space and the reproducing kernel function of the space is given by using the shifted Legendre polynomials as the basis function. It is different from former that this function is no longer a piecewise function, so when the fractional operator is used on the kernel function, the computation is reduced. Thus the approximate solution is more accurate. Finally, the numerical examples illustrate the validity of the method.

Key words: Fractional differential equations, Shifted Legendre polynomials, Reproducing kernel method

中图分类号:

O241.8

巩全壹,么焕民. 再生核移位勒让德基函数法求解分数阶微分方程[J]. 数学物理学报, 2020, 40(2): 441-451.

Quanyi Gong,Huanmin Yao. Reproducing Kernel Shifted Legendre Basis Function Method for Solving the Fractional Differential Equations[J]. Acta mathematica scientia,Series A, 2020, 40(2): 441-451.

表 1

方程(7.1)中 $\alpha$ 取不同值的绝对误差"

	本文所取节点数	文献[5]中所取节点数
$n$	5	8
$\alpha$	本文中的误差	文献[5]中的误差
1.9	5.67888E-07	2.18E-03
1.7	9.49771E-08	2.17E-03
1.5	9.51231E-08	2.16E-03
> 1.2	5.07967E-07	2.16E-03
1.1	3.50476E-04	2.16E-03

表 1

表 2

求解方程(7.2), $n$ 取不同值的绝对误差"

x_n₁	$n_{1} = 6$	$x_{n_{2}}$	$n_{2} = 7$
$\frac{1}{6}$	3.56401E-08	$\frac{1}{7}$	1.44916E-08
$\frac{1}{3}$	3.99251E-08	$\frac{2}{7}$	1.57484E-08
$\frac{1}{2}$	4.35407E-08	$\frac{3}{7}$	1.68102E-08
$\frac{2}{3}$	4.64885E-08	$\frac{4}{7}$	1.76847E-08
$\frac{5}{6}$	4.87702E-08	$\frac{5}{7}$	1.83794E-08

表 2

表 3

方程(7.2)的绝对误差与文献[5]的比较结果"

		$\frac{6}{7}$	1.89021E-08
	本文所取节点数		文献[5]中所取节点数
$n$	6	7	16
绝对误差	4.31271E-08	1.70707E-08	3.07E-04

表 3

图 1

绝对误差 $\mid u_{5}(x)-u(x)\mid$ , $\mid u_{5}'(x)-u'(x)\mid$ "

图 1

图 2

绝对误差 $\mid u_{10}(x)-u(x)\mid$ , $\mid u_{10}'(x)-u'(x)\mid$ "

图 2

1	Singh C S , Singh H , Singh V K , Singh Om P . Fractional order operational matrix methods for fractional singular integro-differential equation. Appl Math Model, 2016, 40, 10705- 10718 doi: 10.1016/j.apm.2016.08.011
2	Rehman M U , Khan R A . A numerical method for solving boundary value problems for fractional differential equations. Appl Math Model, 2012, 36, 894- 907 doi: 10.1016/j.apm.2011.07.045
3	Zahra W K , Van Daele M . Discrete spline methods for solving two point fractional Bagley-Torvik equation. Appl Math Comput, 2017, 296, 42- 56
4	Pedas A , Tamme E , Vikerpuur M . Smoothing transformation and spline collocation for nonlinear fractional initial and boundary value problems. J Comput Appl Math, 2017, 317, 1- 16 doi: 10.1016/j.cam.2016.11.022
5	Karraslan M F , Celiker F , Kurulay M . Approximate solution of the Bagley-Torvik equation by hybridizable discontinuous Galerkin methods. Appl Math Comput, 2016, 285, 51- 58
6	El-Ajou A , Aequb O A , Momani S . Solving fractional two-point boundary value problems using continuous analytic method. Ain Shams Eng J, 2013, 4, 539- 547 doi: 10.1016/j.asej.2012.11.010
7	Hashim I , Abdulaziz O , Momani S . Homotopy analysis method for fractional IVPs. Commun Nonlinear Sci Numer Simul, 2009, 14, 674- 684 doi: 10.1016/j.cnsns.2007.09.014
8	Daftardar-Gejji V , Jafari H . Solving a multi-order fractional differential equation using adomian decomposition. Appl Math Comput, 2007, 189, 541- 548
9	Abdulaziz O, Hashim I, Momani S. Solving systems of fractional differential equations by homotopy-perturbation method. Phys Lett, 2008, A372:451-459
10	Wu G, Lee E W M. Fractional variational iteration method and its application. Phys Lett, 2010, A374:2506-2509
11	Odibat Z , Momani S , Suat Erturk V . Generalized differential transform method:application to differential equations of fractional order. Appl Math Comput, 2008, 197, 467- 477
12	Arikoglu A , Ozkol I . Solution of fractional differential equations by using differential transform method. Chaos Soliton Frac, 2007, 34, 1473- 1481 doi: 10.1016/j.chaos.2006.09.004
13	Reutskiy S Yu . A novel method for solving second order fractional eigenvalue problems. J Comput Appl Math, 2016, 306, 133- 153 doi: 10.1016/j.cam.2016.04.003
14	Zhang Y . A finite difference method for fractional partial differential equation. Appl Math Comput, 2009, 215, 524- 529
15	Daftardar-Gejji V , Jhinga A . A new finite-difference predictor-corrector method for fractional differential equations. Appl Math Comput, 2018, 336, 418- 432
16	Baleanu D , Shiri B . Collocation methods for fractional differential equations involving non-singular kernel. Chaos Soliton Frac, 2018, 116, 136- 145 doi: 10.1016/j.chaos.2018.09.020
17	Ziane D , Baleanu D , Belghaba K , Hamdi Cherif M . Local fractional Sumudu decomposition method for linear partial differential equations with local fractional derivative. Journal of King Saud University-Science, 2019, 31, 83- 88 doi: 10.1016/j.jksus.2017.05.002
18	Zhou Y T , Zhang C J . Convergence and stability of block boundary value methods applied to nonlinear fractional differential equations with Caputo derivatives. Appl Numer Math, 2019, 135, 367- 380 doi: 10.1016/j.apnum.2018.09.010
19	Mohammadi F , Cattani C . A generalized fractional-order Legendre wavelet Tau method for solving fractional differential equations. J Comput Appl Math, 2018, 339, 306- 316 doi: 10.1016/j.cam.2017.09.031
20	Bakhtiari P , Abbasbanda S , Van Gorder R A . Reproducing kernel method for the numerical solution of the 1D Swift-Hohenberg equation. Appl Math Comput, 2018, 339, 132- 143
21	Niu J , Xu M Q , Yao G M . An efficient reproducing kernel method for solving the Allen-Cahn equation. Appl Math Lett, 2019, 89, 78- 84 doi: 10.1016/j.aml.2018.09.013
22	Mei L C , Lin Y Z . Simplified reproducing kernel method and convergence order for linear Volterra integral equations with variable coefficients. J Comput Appl Math, 2019, 346, 390- 398 doi: 10.1016/j.cam.2018.07.027
23	Li X Y , Wu B Y . A numerical technique for variable fractional functional boundary value problems. Appl Math Lett, 2015, 43, 108- 113 doi: 10.1016/j.aml.2014.12.012
24	Yang J B , Yao H M , Wu B Y . An efficient numerical method for variable order fractional functional differential equation. Appl Math Lett, 2018, 76, 221- 226 doi: 10.1016/j.aml.2017.08.020
25	Geng F Z , Cui M G . A reproducing kernel method for solving nonlocal fractional boundary value problem. Appl Math Lett, 2012, 25, 818- 823 doi: 10.1016/j.aml.2011.10.025
26	Li X Y , Wu B Y . A new reproducing kernel method for variable order fractional boundary value problems for functional differential equations. J Comput Appl Math, 2017, 311, 387- 393 doi: 10.1016/j.cam.2016.08.010
27	Xu M Q , Lin Y Z . Simplified reproducing kernel method for fractional differential equations with delay. Appl Math Lett, 2016, 52, 156- 161 doi: 10.1016/j.aml.2015.09.004
28	Li X Y , Li H , Wu B Y . A new numerical method for variable order fractional functional differential equations. Appl Math Lett, 2017, 68, 80- 86 doi: 10.1016/j.aml.2017.01.001
29	张禾瑞, 郝鈵新. 高等代数(第五版). 北京: 高等教育出版社, 2007
	Zhang H R , Hao B X . Advanced Algebra (Fifth Edition). Beijing: Higher Education Press, 2007
30	吴勃英, 林迎珍. 应用型再生核空间. 北京: 科学出版社, 2012
	Wu B Y , Lin Y Z . Application of the Reproducing Kernel Space. Beijing: Science Press, 2012

Just accepted

Online first

Just accepted

Online first

Viewed

Full text

From	Others	local

Times	2	84
Rate	2%	98%

Abstract

Just accepted	Online first	Issue

0	0	80

From	Others	local

Times	78	2
Rate	98%	2%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed

[1]	王春. 一类分数阶系统的稳定性和Laplace变换[J]. 数学物理学报, 2019, 39(1): 49-58.
[2]	王惠文, 曾红娟, 李芳. 多基点分数阶微分方程脉冲边值问题解的存在性[J]. 数学物理学报, 2018, 38(4): 697-715.
[3]	Marko Kostić, 李成刚, 李淼. 抽象多项Riemann-Liouville分数阶微分方程[J]. 数学物理学报, 2016, 36(4): 601-622.
[4]	胡雷, 张淑琴, 侍爱玲. 分数阶微分方程耦合系统共振边值问题解的存在性[J]. 数学物理学报, 2014, 34(5): 1313-1326.
[5]	郝晓红, 程智龙, 周宗福. 一类非线性分数阶多点边值问题的可解性[J]. 数学物理学报, 2014, 34(3): 655-668.
[6]	舒小保, 戴斌祥. 半线性中立型分数阶微分方程S -渐近ω周期解[J]. 数学物理学报, 2014, 34(1): 16-26.
[7]	王永庆, 刘立山. Banach 空间中分数阶微分方程 $m$ 点边值问题的正解[J]. 数学物理学报, 2012, 32(1): 246-256.
[8]	许晓婕, 孙新国, 吕炜. 非线性分数阶微分方程边值问题正解的存在性[J]. 数学物理学报, 2011, 31(2): 401-409.