数学物理学报, 2020, 40(1): 49-62 doi:

论文

带群集耗散项的零压流方程的扰动黎曼问题

张庆玲, 巴英

The Perturbed Riemann Problem for the Pressureless Euler Equations with a Flocking Dissipation

Zhang Qingling, Ba Ying

收稿日期: 2018-05-15  

基金资助: 武汉市教育局教学研究重点项目.  2017007

Received: 2018-05-15  

Fund supported: 武汉市教育局教学研究重点项目.  2017007

作者简介 About authors

张庆玲 。

摘要

该文通过分析带群集耗散项的零压流方程初始波含狄拉克激波的波的相互作用，研究了其初值含三片常值和初值含狄拉克测度的两种扰动黎曼问题.当初值为三片常值时，通过广义Rankine-Hugoniot条件和广义熵条件，该文构造性地得到了整体解.进一步地，利用弱解的稳定性理论，通过分析初值为三片常值情形下解的结构并取极限，该文得到了初值含狄拉克测度的扰动黎曼问题的整体解.另外，在构造解的过程中，还引入了一种新的非经典解：狄拉克接触间断解.

关键词： 零压流 ; 黎曼问题 ; 狄拉克激波 ; 真空 ; 群集耗散 ; 波的相互作用

Abstract

In this paper, the wave interactions involving the delta shock waves for the pressureless Euler equations with a flocking dissipation is considered and two kinds of perturbed Riemann problems are studied. The global existence of the generalzied solutions is obtained constructively by using the generalized Rankine-Hugoniot conditions and the entropy condition when the initial data are three piecewise constant states. By analyzing the global structure and the limit under the stability theory of weak solutions, the global soution for the delta inital data problem are constructively obtained. Moreover, a new kind of nonclassical wave -delta contact discontinuity has appeared in it.

Keywords： Pressureless Euler equations ; Riemann problem ; Delta shock wave ; Vacuum state ; Flocking dissipation ; Interaction

PDF (464KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张庆玲, 巴英. 带群集耗散项的零压流方程的扰动黎曼问题. 数学物理学报[J], 2020, 40(1): 49-62 doi:

Zhang Qingling, Ba Ying. The Perturbed Riemann Problem for the Pressureless Euler Equations with a Flocking Dissipation. Acta Mathematica Scientia[J], 2020, 40(1): 49-62 doi:

1 引言

在本文中,我们考虑如下的非齐次零压流方程组

$ \begin{equation} \left\{\begin{array}{ll} \rho_t+(\rho u)_x = 0, \\ (\rho u)_t+(\rho u^2)_x = -\rho u, \end{array}\right. \end{equation} $

其中$ \rho $和$ u $分别表示密度和速度.

模型(1.1)是群体运动模型Cucker-Smale模型趋于平衡态时的动力学描述,其详细推导可参考文献[8].目前已经得到关于该模型的一些适定性结果[8, 11-12]. Cucker-Smale模型是描述群体现象的一个离散模型,其动力学方面的研究近年来受到了广泛关注,比如文献[9]中关于渐近行为和稳定性的研究.

当(1.1)式右端的非齐次项为零时,它就是人们常见的零压流模型(输运方程).该模型是研究狄拉克激波($ \delta $ -激波)和真空形成的最重要模型.自1994年起,它便被人们广泛研究,见文献[1, 6, 10, 15, 20, 23-24]等.特别地, Bouchut首次给出了其黎曼问题测度解的存在性[1],丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性[10, 23-24].

对于模型(1.1), Ha,黄飞敏和王益等在2014年首次推导出了该模型,并通过引入广义势得到了当初值$ \rho_{0}\in L_{loc}^{1}({\Bbb R}) $, $ u_{0}\in L^{\infty}({\Bbb R}) $时其整体熵解的存在性和唯一性[8].随后,金春银将他们的结果推广到$ \rho_{0} $是Radon测度, $ u_{0}\in L^{\infty}(\rho_{0}) $的情形[12],并得到了该模型在Wasserstein空间的适定性[11].

对于模型(1.1)的黎曼问题,我们知道$ \delta $ -激波和真空确实会出现[8, 11].另外,基本波的相互作用在理论、数值计算和应用方面都起着很重要的作用.因此,本文中我们主要研究模型(1.1)初值含$ \delta $ -测度的扰动黎曼问题和包含$ \delta $ -激波和真空的所有可能的波的相互作用,即我们重点关注模型(1.1)的如下初值问题

$ \begin{equation} (\rho, u)(x, 0) = \left\{\begin{array}{ll} (\rho_-, u_-), \ \ \ \ \ x<0, \\ (m_0\delta, u_0), \ \ \ \ x = 0, \\ (\rho_+, u_+), \ \ \ \ \ x>0, \end{array}\right. \end{equation} $

其中$ \delta $是标准的狄拉克函数, $ m_0 $, $ u_0 $, $ \rho_\pm $和$ u_\pm $是任意常数.因为模型(1.1)的黎曼解中出现了$ \delta $ -激波,很自然地我们要考虑其初值含$ \delta $ -测度的初值问题(1.2).对于零压流、Chaplygin气体方程和其他方程类似初值问题的研究,可参考文献[6, 15, 25-27].

本文中,为解决初值问题(1.1)–(1.2),我们首先考虑如下的扰动黎曼问题

$ \begin{equation} (\rho, u)(x, 0) = \left\{\begin{array}{ll} (\rho_-, u_-), \ \ \ \ x<-\epsilon, \\ (\frac{m_0}{2\epsilon}, u_0), \ \ \ \ -\epsilon<x<\epsilon, \\ (\rho_+, u_+), \ \ \ \ \ x>\epsilon, \end{array}\right. \end{equation} $

其中$ \epsilon $是充分小的正数.我们构造出了问题(1.1), (1.3)的整体解,并得到了其大时间渐近行为.而且,在构造解的过程中,我们还发现了一种新的非经典解:$ \delta $ -接触间断解. $ \delta $ -接触间断是一种包含$ \delta $ -函数形式的解,其支集在接触间断上.该形式的非经典解曾出现在磁流体力学方程和零压流的基本波的相互作用过程中[16, 19].

接下来,令$ \epsilon\rightarrow0 $,由弱解的稳定性理论,并结合广义Rankine-Hugoniot条件和广义熵条件,我们构造性地得到了模型(1.1)–(1.2)的唯一整体解.而且,其解中也包含了$ \delta $ -接触间断.进一步地,取$ m_{0} = 0 $, $ u_{0} = 0 $,模型(1.1)–(1.2)的解正好对应于(1.1)的黎曼解.在文献[25]中,作者和其导师首次应用本文中构造解的方法成功解决了一维Chaplygin气体初值含$ \delta $ -函数的初值问题.近年来,该方法已经被应用于研究很多相关方程组的类似问题[7, 22].

在文献[23]和[24]中,丁夏畦,黄飞敏和王振研究了齐次的零压流方程

$ \begin{equation} \left\{\begin{array}{ll} \rho_t+(\rho u)_x = 0, \\ (\rho u)_t+(\rho u^2)_x = 0, \end{array}\right. \end{equation} $

证明了其初值为可测函数时柯西问题弱解的存在性和唯一性.紧接着,在文献[10]中,黄飞敏和王振又将结果推广到初值为Radon测度的情形.此后,对于含各种形式非齐次项的零压流方程陆续有了相关研究结果[2, 5, 17].在这些文献的基础上,本文给出了初值问题(1.1)–(1.2)弱解的存在性,唯一性和大时间渐近行为等方面新的结果.在后面的研究中,作者还将在本文研究基础上进一步考虑含间断非齐次项的零压流的初值问题.

本文安排如下:在第2部分,我们给出了本文的预备知识,并展示了模型(1.1)的黎曼解;在第3部分,我们首先分四种情形构造出了初值问题(1.1), (1.3)的整体解,然后令$ \epsilon\rightarrow0 $,由弱解的稳定性理论,并结合广义Rankine-Hugoniot条件和广义熵条件,得到了初值问题(1.1)–(1.2)的整体解和大时间渐近行为;第4部分给出了本文结论.

2 预备知识

在这一部分,我们将考虑模型(1.1)含如下初值的黎曼问题

$ \begin{equation} (\rho, u)(x, 0) = (\rho_\pm, u_\pm), \ \ \ \ \pm x>0, \end{equation} $

对于光滑解,模型(1.1)等价于

$ \begin{equation} \left\{\begin{array}{ll} \rho_t+(\rho u)_x = 0, \\ u_t+uu_x = -u. \end{array}\right. \end{equation} $

该方程组是非严格双曲的,具有两个相同的特征值$ \lambda_1 = \lambda_2 = u $,且$ \lambda_1, \lambda_2 $是线性退化的.

(2.2)式的特征方程为

$ \begin{equation} \frac{{\rm d}x}{{\rm d}t} = u, \ \ \frac{{\rm d}\rho}{{\rm d}t} = -\rho u_x, \ \ \frac{{\rm d}u}{{\rm d}t} = -u. \end{equation} $

因此,在特征线相交之前,沿着特征线$ (\rho, u) $的值分别为

$ \begin{equation} \rho = \rho_{-}, \ \ u = u_-e^{-t}, \ \ x = x_0+u_-(1-e^{-t}), \ \ x_{0}<0. \end{equation} $

$ \begin{equation} \rho = \rho_{+}, \ \ u = u_+e^{-t}, \ \ x = x_0+u_+(1-e^{-t}), \ \ x_{0}>0. \end{equation} $

接下来,我们将分三种情形来构造模型(1.1)的黎曼解.

情形一   $ u_{-} = u_{+} $.这种情形中,左状态$ (\rho_-, u_-e^{-t}) $和右状态$ (\rho_+, u_+e^{-t}) $通过接触间断$ J:x = u_-(1-e^{-t}) = u_+(1-e^{-t}) $连接,因此,黎曼解为

$ \begin{equation} (\rho, u)(x, t) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t}), \ \ &x<u_-(1-e^{-t}), \\ (\rho_+, u_+e^{-t}), \ \ &x>u_+(1-e^{-t}). \end{array}\right. \end{equation} $

情形二   $ u_{-}<u_{+} $.这种情形中,很容易看到从原点$ (0, 0) $出发的两条特征线$ x = u_-(1-e^{-t}) $和$ x = u_+(1-e^{-t}) $之间的点不在任何一条从$ x $轴出发的特征线上.因此,在区域$ D = \{(x, t):u_-(1-e^{-t})<x<u_+(1-e^{-t}), 0<t<\infty\} $内部会出现真空,此时黎曼解为

$ \begin{equation} (\rho, u)(x, t) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t}), \ \ & x<u_-(1-e^{-t}), \\ (0, u_*e^{-t}), \ \ \ \ &u_-(1-e^{-t})<x<u_+(1-e^{-t}), \\ (\rho_+, u_+e^{-t}), \ \ &x>u_+(1-e^{-t}), \end{array}\right. \end{equation} $

其中$ u_{-}<u_*<u_{+} $.此处类似于文献[19],我们将真空视为特殊的稀疏波解,从而对它赋予了伪速度:特征线速度.本文中对真空我们都将这样处理,后面不再赘述.

情形三   $ u_{-}>u_{+} $.这种情形中,很容易看到从左状态发出的特征线和从右状态发出的特征线将会相交,从而形成非经典解:$ \delta $ -激波.为了在非经典解的框架下求解黎曼问题(1.1), (2.1),类似于文献[17],我们将引入支集在一条曲线上的加权$ \delta $ -测度解.

定义2.1  为定义测度解,一个支集在光滑曲线$ S = \{(x(s), t(s)):a<s<b\} $上的二维加权$ \delta $-测度$ p(s)\delta_S $可定义如下

对任何的$ \psi\in C_0^\infty({\Bbb R}\times {\Bbb R}_{+}) $都成立.

为方便起见,我们选择参数$ s = t $,并用$ w(t) = \sqrt{1+{x'(t)}^2}p(t) $来表示$ \delta $ -激波的强度(质量).接下来,我们将给出黎曼问题(1.1), (2.1)的$ \delta $ -激波解的定义.该定义框架由Danilov和Shelkovich[3-4]提出,并经Kalisch和Mitrovic[13-14]发展而来.

定义2.2  假设$ (\rho, u) $是一对分布函数, $ \rho $具有如下形式

$ \begin{equation} \rho(x, t) = \hat{\rho}(x, t)+w(x, t)\delta(S), \end{equation} $

其中$ \hat{\rho}, w\in L^{\infty}({\Bbb R}\times {\Bbb R}^{+}) $,如果它们对任意的$ \psi\in C_0^\infty({\Bbb R}\times {\Bbb R}^{+}) $满足

$ \begin{equation} \left\{\begin{array}{ll} \langle\rho, \psi_{t}\rangle+\langle\rho u, \psi_{x}\rangle = 0, \\ \langle\rho u, \psi_{t}\rangle+\langle\rho u^{2}, \psi_{x}\rangle = \langle\rho u, \psi\rangle, \end{array}\right. \end{equation} $

则称它们是黎曼问题(1.1), (2.1)的$ \delta $ -激波解.这里

符号$ S $表示$ \delta $ -激波曲线, $ u_{\delta}(t) $是$ u $在$ \delta $ -激波上的取值.

在上述定义下,如果$ u_{-}>u_{+} $,黎曼问题(1.1), (2.1)具有如下形式的分片光滑解

$ \begin{equation} (\rho, u)(x, t) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t}), \ \ \ \ \ \ \ \ \ \ \ & x<x(t), \\ (w(t)\delta(x-x(t)), u_{\delta}(t)), \ \ &x = x(t), \\ (\rho_+, u_+e^{-t}), \ \ \ \ \ \ \ \ \ \ \ \ &x>x(t), \end{array}\right. \end{equation} $

其中$ x(t) $, $ w(t) $和$ \sigma(t) = x'(t) $分别表示$ \delta $ -激波的位置、质量和传播速度.

很容易证明,黎曼问题(1.1), (2.1)的形如(2.10)式的$ \delta $ -激波解应满足如下的广义Rankine-Hugoniot条件

$ \begin{equation} \left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t} = \sigma = u_{\delta}, \\ \frac{{\rm d}w}{{\rm d}t} = \sigma[\rho]-[\rho u]e^{-t}, \\ \frac{{\rm d}(wu_{\delta})}{{\rm d}t}+wu_{\delta} = \sigma[\rho u]e^{-t}-[\rho u^{2}]e^{-2t} \end{array}\right. \end{equation} $

和初值条件

$ \begin{equation} (x, w)|_{t = 0} = (0, 0), \end{equation} $

这里$ [\rho] = \rho_+-\rho_- $.广义Rankine-Hugoniot条件的推导可参考文献[17-18, 21],此处从略.另外,为保证黎曼解的唯一性, $ \delta $ -激波还应满足如下的广义熵条件

$ \begin{equation} u_{+}e^{-t}<u_{\delta}<u_{-}e^{-t}, \end{equation} $

这表示$ \delta $ -激波两侧的所有特征线都将进入$ \delta $ -激波.

下面我们来求解初值问题(2.11)–(2.12),假设$ \rho_\pm $不全为0.

积分(2.11)式,并利用初值条件(2.12),我们得到

$ \begin{equation} \left\{\begin{array}{ll} w = [\rho ]x+[\rho u](e^{-t}-1), \\ w u_ \delta e^t = [\rho u]x+[\rho u^2](e^{-t}-1). \end{array}\right. \end{equation} $

即

$ \begin{equation} [\rho]xu_\delta e^t+[\rho u](e^{-t}-1)u_\delta e^t = [\rho u]x+[\rho u^2](e^{-t}-1). \end{equation} $

将(2.15)式两边乘以$ e^{-t} $,我们得到

即

$ \begin{equation} \frac{\rm d}{{\rm d}t}(\frac{1}{2}[\rho]x^2+[\rho u](e^{-t}-1)x) = [\rho u^2](e^{-2t}-e^{-t}). \end{equation} $

将(2.16)式从$ 0 $到$ t $积分,可得

$ \begin{equation} [\rho]x^2+2[\rho u](e^{-t}-1)x+[\rho u^2](e^{-t}-1)^2 = 0. \end{equation} $

当$ [\rho] = 0 $时,易得$ x(t) = \frac{u_-+u_+}{2}(1-e^{-t}) $.

当$ [\rho]\neq0 $时,解关于$ x(t) $的一元二次方程(2.17)可得

由熵条件(2.13)知,上式中只能取正号,即

综上可得

即

$ \begin{equation} x(t) = \sigma_0(1-e^{-t}), \end{equation} $

其中

$ \begin{equation} \sigma_0 = \frac{\sqrt{\rho_-}u_-+\sqrt{\rho_+}u_+}{\sqrt{\rho_-}+\sqrt{\rho_+}}. \end{equation} $

从(2.11)和(2.14)式的第一个方程可得

$ \begin{equation} u_\delta(t) = \sigma e^{-t}, \end{equation} $

$ \begin{equation} w(t) = \sqrt{\rho_-\rho_+}(u_–u_+)(1-e^{-t}). \end{equation} $

所以,当$ u_{-}>u_{+} $时,黎曼问题(1.1), (2.1)解可由(2.10)式给出,其中$ x(t), u_\delta(t) $和$ w(t) $分别由(2.18)–(2.21)式给出.

3 扰动黎曼问题

在这一部分,我们首先构造初值问题(1.1), (1.3)的整体解,然后令$ \epsilon\rightarrow0 $,根据弱解的稳定性理论,得到问题(1.1), (1.2)的整体解.接下来,根据从$ (-\epsilon, 0) $和$ (\epsilon, 0) $发出的波的不同组合,我们将分如下四种情形进行讨论: (1) $ u_-\leq u_0\leq u_+ $; (2) $ u_+< u_0<u_- $; (3) $ u_0< u_-< u_+(u_-< u_+< u_0) $; (4) $ u_0< u_+< u_-(u_+< u_-< u_0) $.

情形3.1   $ u_-\leq u_0\leq u_+ $ ($ u_-\neq u_+ $)

根据$ u_0 $的值的大小,我们接下来分下面三种子情形来讨论.

子情形3.1.1    $ u_-<u_0<u_+ $.

对任何时刻$ t $,问题(1.1), (1.3)的解可表示如下(见图 3.1(a))

其中"$ + $"表示"复合", "Vac."代表"真空".由于$ \widetilde{J_1^0} $和$ \widetilde{J_2^0} $的传播速度均为$ u_0e^{-t} $,所以$ \widetilde{J_1^0} $和$ \widetilde{J_2^0} $永远不会相交.令$ \epsilon\rightarrow0 $,我们得到问题(1.1), (1.2)的解可表示如下(见图 3.1(b))

其中, $ \delta J $的传播速度为$ u_0e^{-t} $, "$ (\pm) $"代表"$ (\rho_{\pm}, u_{\pm}e^{-t}) $", "$ (0) $"代表"$ (\frac{m_{0}}{2\epsilon}, u_{0}e^{-t}) $".这里的$ \delta J $是一种新的非经典波:$ \delta $ -接触间断,即$ \delta $ -函数支集在接触间断上,此类波在文献[16, 19]中也有出现.很容易验证$ \delta J $满足广义Rankine-Hugoniot条件(2.11)和初值条件$ (x, w, u_\delta)(0) = (0, m_0, u_0), $其中$ \rho_- = \rho_+ = 0 $.

图 3.1

新窗口打开| 下载原图ZIP| 生成PPT

图 3.1   </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p id="C60">子情形3.1.2   <span class="formulaText"><inline-formula><tex-math id="M141">$ u_- = u_0<u_+ $</tex-math></inline-formula></span><span class="formulaNumber">.</span>类似于子情形3.1.1,此时问题(1.1), (1.2)的解如<a class="table-icon" style="color:#2150f9" href="#Fig3.2"; id="inline_content图 3.2(a)">图 3.2(a)</a>.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C61">子情形3.1.3   <span class="formulaText"><inline-formula><tex-math id="M142">$ u_-<u_0 = u_+ $</tex-math></inline-formula></span><span class="formulaNumber">.</span>类似于子情形3.1.2,此时问题(1.1), (1.2)的解如<a class="table-icon" style="color:#2150f9" href="#Fig3.2"; id="inline_content图 3.2(b)">图 3.2(b)</a>.</p> </div> </div> <h3 style="position: absolute; opacity: 0; filter:Alpha(opacity=0);">图 3.2</h3> <div class="content-zw-img" id=""> <div class="content-zw-img-img figure outline_anchor" onmouseleave="likai(this);"> <img src="sxwlxb-40-1-49-3.2.jpg" onclick="clickss(this)" onmouseover="huoqukuanduimg(this);" class="tupian"> <p class="tishi"> <a href="sxwlxb-40-1-49-3.2.jpg.html" target="_blank">新窗口打开</a>| <a href="sxwlxb-40-1-49-3.2.jpg.zip">下载原图ZIP</a>| <a href="sxwlxb-40-1-49-3.2.jpg.ppt">生成PPT</a> </p> </div> <div class="content-zw-img-shuoming"> <p class="content-zw-img-shuoming-title-cn"><b>图 3.2   <title/> </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p id="C62">如果<span class="formulaText"><inline-formula><tex-math id="M151">$ m_0 = 0, u_0 = 0 $</tex-math></inline-formula></span>,很容易验证问题(1.1), (1.2)的解就是黎曼问题(1.1), (2.1)的解,从而反映了我们构造的解关于黎曼初值的小扰动是稳定的.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C63"><strong>情形3.2</strong>   <span class="formulaText"><inline-formula><tex-math id="M152">$ u_+< u_0<u_- $</tex-math></inline-formula></span></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C64">在这种情形,当时间<span class="formulaText"><inline-formula><tex-math id="M153">$ t $</tex-math></inline-formula></span>足够小(设<span class="formulaText"><inline-formula><tex-math id="M154">$ t $</tex-math></inline-formula></span>小于某一临界时刻<span class="formulaText"><inline-formula><tex-math id="M155">$ t_1 $</tex-math></inline-formula></span><span class="formulaNumber">)</span>时,问题(1.1), (1.3)的解可表示如下(见<a class="table-icon" style="color:#2150f9" href="#Fig3.3"; id="inline_content图 3.3(a)">图 3.3(a)</a>)</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE10"> $ (\rho_-, u_-e^{-t})+\widetilde{\delta S_{1}}+(\frac{m_0}{2\epsilon}, u_0e^{-t})+ \widetilde{\delta S_{2}}+(\rho_+, u_+e^{-t}), $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C65">这里<span class="formulaText"><inline-formula><tex-math id="M156">$ \widetilde{\delta S_{1}} $</tex-math></inline-formula></span>的传播速度为<span class="formulaText"><inline-formula><tex-math id="M157">$ u_\delta ^{1} $</tex-math></inline-formula></span>,其中<span class="formulaText"><inline-formula><tex-math id="M158">$ u_0e^{-t}<u_\delta ^{1} = \sigma_1e^{-t}<u_-e^{-t} $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M159">$ \sigma_1 = \frac{\sqrt{\rho_-}u_-+\sqrt{\frac{m_0}{2\epsilon}}u_0}{\sqrt{\rho_-}+\sqrt{\frac{m_0}{2\epsilon}}} $</tex-math></inline-formula></span><span class="formulaNumber">.</span> <span class="formulaText"><inline-formula><tex-math id="M160">$ \widetilde{\delta S_{2}} $</tex-math></inline-formula></span>的传播速度为<span class="formulaText"><inline-formula><tex-math id="M161">$ u_\delta ^{2} $</tex-math></inline-formula></span>,其中<span class="formulaText"><inline-formula><tex-math id="M162">$ u_+e^{-t}<u_\delta ^{2} = \sigma_2e^{-t}<u_0e^{-t} $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M163">$ \sigma_2 = \frac{\sqrt{\rho_, +}u_++\sqrt{\frac{m_0}{2\epsilon}}u_0}{\sqrt{\rho_+}+\sqrt{\frac{m_0}{2\epsilon}}} $</tex-math></inline-formula></span><span class="formulaNumber">.</span>因此, <span class="formulaText"><inline-formula><tex-math id="M164">$ \widetilde{\delta S_{1}} $</tex-math></inline-formula></span>将会在<span class="formulaText"><inline-formula><tex-math id="M165">$ t_1 $</tex-math></inline-formula></span>时刻超过<span class="formulaText"><inline-formula><tex-math id="M166">$ \widetilde{\delta S_{2}} $</tex-math></inline-formula></span>,其交点<span class="formulaText"><inline-formula><tex-math id="M167">$ (x_1, t_1) $</tex-math></inline-formula></span>由下式决定</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE11"> $ \left\{\begin{array}{ll} x_1+\epsilon = \sigma_1(1-e^{-t_1}), \\ x_1-\epsilon = \sigma_2(1-e^{-t_1}), \end{array}\right. $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C66">即</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE12"> $ (x_1, t_1) = \bigg(\frac{\epsilon(\sigma_1+\sigma_2)}{\sigma_1-\sigma_2}, -\ln{(1-\frac{2\epsilon}{\sigma_1-\sigma_2})} \bigg). $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C67">显然当<span class="formulaText"><inline-formula><tex-math id="M168">$ \epsilon\rightarrow0 $</tex-math></inline-formula></span>时, <span class="formulaText"><inline-formula><tex-math id="M169">$ (x_1, t_1)\rightarrow(0, 0) $</tex-math></inline-formula></span><span class="formulaNumber">.</span></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C68">在<span class="formulaText"><inline-formula><tex-math id="M170">$ t = t_1 $</tex-math></inline-formula></span>时刻,我们将面对问题(1.1)带如下初值的新的初值问题</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.1)</label><tex-math id="E3.1"> $ \begin{equation} (\rho, u)(x, t_1) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t_1}), \ \ \ \ \ \ & x<x_1, \\ (w(t_1)\delta(x-x_1), \widetilde{u_\delta^0}), \ \ & x = x_1, \\ (\rho_+, u_+e^{-t_1}), \ \ \ \ \ \ & x>x_1, \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C69">其中</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE13"> $ w(t_1) = \widetilde{w^1}(t_1)+\widetilde{w^2}(t_1), \ \ w(t_1)\widetilde{u_\delta^0} = \widetilde{w^1}(t_1)u_\delta^1(t_1)+\widetilde{w^2}(t_1)u_\delta^2(t_1). $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C70">此时,同解<span class="formulaText"><inline-formula><tex-math id="M171">$ t = 0 $</tex-math></inline-formula></span>时刻的初值问题(1.1), (1.2)一样,我们构造问题(1.1), (3.1)的类似于问题(1.1), (1.3)的扰动黎曼问题,从而将解延拓到某一时刻<span class="formulaText"><inline-formula><tex-math id="M172">$ t = t_2>t_1 $</tex-math></inline-formula></span><span class="formulaNumber">.</span>接下来,不断重复上述过程,一直到<span class="formulaText"><inline-formula><tex-math id="M173">$ t\rightarrow\infty $</tex-math></inline-formula></span>,从而构造出初值问题(1.1), (1.3)的整体解如下</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE14"> $ (\rho_-, u_-e^{-t})+\widetilde{\delta S_{3}}+(\rho_+, u_+e^{-t}). $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C71">最后,令<span class="formulaText"><inline-formula><tex-math id="M174">$ \epsilon\rightarrow0 $</tex-math></inline-formula></span>时,可得到初值问题(1.1), (1.2)具有如下形式的整体解(见<a class="table-icon" style="color:#2150f9" href="#Fig3.3"; id="inline_content图 3.3(b)">图 3.3(b)</a>)</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE15"> $ (\rho_-, u_-e^{-t})+\delta S+(\rho_+, u_+e^{-t}). $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C72">即</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.2)</label><tex-math id="E3.2"> $ \begin{equation} (\rho, u)(x, t) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t}), \ \ \ \ \ \ \ \ \ & x<x(t), \\ (w(t)\delta(x-x(t)), u_\delta(t)), \ \ & x = x(t), \\ (\rho_+, u_+e^{-t}), \ \ \ \ \ \ \ \ \ &x>x(t), \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C73">且满足广义Rankine-Hugoniot条件</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.3)</label><tex-math id="E3.3"> $ \begin{equation} \left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t} = u_\delta, \\ \frac{{\rm d}w}{{\rm d}t} = [\rho] u_\delta-[\rho u]e^{-t}, \\ \frac{{\rm d}(w u_ \delta)}{{\rm d}t}+{w u_ \delta} = [\rho u] u_\delta e^{-t}-[\rho u^2]e^{-2t} \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C74">和初值条件</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.4)</label><tex-math id="E3.4"> $ \begin{equation} (x, w, u_\delta)|_{t = 0} = (0, m_0, u_0), \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C75">这里<span class="formulaText"><inline-formula><tex-math id="M175">$ [\rho] = \rho_+-\rho_- $</tex-math></inline-formula></span><span class="formulaNumber">.</span></p> </div> </div> <h3 style="position: absolute; opacity: 0; filter:Alpha(opacity=0);">图 3.3</h3> <div class="content-zw-img" id=""> <div class="content-zw-img-img figure outline_anchor" onmouseleave="likai(this);"> <img src="sxwlxb-40-1-49-3.3.jpg" onclick="clickss(this)" onmouseover="huoqukuanduimg(this);" class="tupian"> <p class="tishi"> <a href="sxwlxb-40-1-49-3.3.jpg.html" target="_blank">新窗口打开</a>| <a href="sxwlxb-40-1-49-3.3.jpg.zip">下载原图ZIP</a>| <a href="sxwlxb-40-1-49-3.3.jpg.ppt">生成PPT</a> </p> </div> <div class="content-zw-img-shuoming"> <p class="content-zw-img-shuoming-title-cn"><b>图 3.3   <title/> </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p id="C76">显然, (3.3)式等价于</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.5)</label><tex-math id="E3.5"> $ \begin{equation} \left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t} = u_\delta, \\ \frac{{\rm d}w}{{\rm d}t} = [\rho] u_\delta-[\rho u]e^{-t}, \\ \frac{{\rm d}(w u_ \delta e^t)}{{\rm d}t} = [\rho u] u_\delta-[\rho u^2]e^{-t}. \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C77">利用初值条件(3.4),积分(3.5)式可得</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.6)</label><tex-math id="E3.6"> $ \begin{equation} \left\{\begin{array}{ll} w = m_0+[\rho ]x+[\rho u](e^{-t}-1), \\ w u_ \delta e^t = m_0u_0+[\rho u]x+[\rho u^2](e^{-t}-1). \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C78">消去<span class="formulaText"><inline-formula><tex-math id="M188">$ w $</tex-math></inline-formula></span>可得</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.7)</label><tex-math id="E3.7"> $ \begin{equation} m_0u_\delta e^t+[\rho]xu_\delta e^t+[\rho u](e^{-t}-1)u_\delta e^t = m_0u_0+[\rho u]x+[\rho u^2](e^{-t}-1). \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C79">(3.7)式两边乘以<span class="formulaText"><inline-formula><tex-math id="M189">$ e^{-t} $</tex-math></inline-formula></span>,可得</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE16"> $ m_0u_\delta+[\rho]xu_\delta+[\rho u](e^{-t}-1)u_\delta = m_0u_0e^{-t}+[\rho u]e^{-t}x+[\rho u^2](e^{-t}-1)e^{-t}, $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C80">即</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.8)</label><tex-math id="E3.8"> $ \begin{equation} \frac{\rm d}{{\rm d}t}(\frac{1}{2}[\rho]x^2+[\rho u](e^{-t}-1)x+m_0x) = m_0u_0e^{-t}+[\rho u^2](e^{-t}-1)e^{-t}. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C81">将(3.8)式从<span class="formulaText"><inline-formula><tex-math id="M190">$ 0 $</tex-math></inline-formula></span>到<span class="formulaText"><inline-formula><tex-math id="M191">$ t $</tex-math></inline-formula></span>积分,可得</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.9)</label><tex-math id="E3.9"> $ \begin{equation} [\rho]x^2+2([\rho u](e^{-t}-1)+m_0)x+2m_0u_0(e^{-t}-1)+[\rho u^2](e^{-t}-1)^2 = 0. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C82">当<span class="formulaText"><inline-formula><tex-math id="M192">$ [\rho] = 0 $</tex-math></inline-formula></span>时,有</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE17"> $ x(t) = \frac{-2m_0u_0(e^{-t}-1)-[\rho u^2](e^{-t}-1)^2}{2([\rho u](e^{-t}-1)+m_0)}. $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C83">当<span class="formulaText"><inline-formula><tex-math id="M193">$ [\rho]\neq0 $</tex-math></inline-formula></span>时,有</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE18"> $ \begin{eqnarray*} &&x(t)\nonumber\\ && = \frac{-([\rho u](e^{-t}-1)+m_0)\pm\{([\rho u](e^{-t}-1)+m_0)^2-[\rho](2m_0u_0(e^{-t}-1)+[\rho u^2](e^{-t}-1)）^2\}^\frac{1}{2}}{[\rho]}\nonumber\\ && = \frac{-([\rho u](e^{-t}-1)+m_0)\pm\{m_0^2+2m_0(-[\rho]u_0+[\rho u])(e^{-t}-1)+\rho_1\rho_2 [u]^2(e^{-t}-1)^2\}^\frac{1}{2}}{[\rho]}.\nonumber \end{eqnarray*} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C84">结合(3.6)式中的第一个等式可知,上式中只能取正号,即</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.10)</label><tex-math id="E3.10"> $ \begin{equation} x(t) = \left\{\begin{array}{ll} \frac{-2m_0u_0(e^{-t}-1)-[\rho u^2](e^{-t}-1)^2}{2([\rho u](e^{-t}-1)+m_0)}, \ \ & [\rho] = 0, \\ \frac{-([\rho u](e^{-t}-1)+m_0)+w(t)}{[\rho]}, \ \ \ \ \ \ & [\rho]\neq0, \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C85">其中</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.11)</label><tex-math id="E3.11"> $ \begin{equation} w(t) = \{m_0^2+2m_0(-[\rho]u_0+[\rho u])(e^{-t}-1)+\rho_1\rho_2 [u]^2(e^{-t}-1)^2\}^\frac{1}{2}. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C86">由(3.6)式的第二个等式可得</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.12)</label><tex-math id="E3.12"> $ \begin{equation} u_\delta(t) = \frac{1}{w(t)e^t}\{m_0u_0+[\rho u]x+[\rho u^2](e^{-t}-1)\}. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C87">综上可知,在此种情形下,初值问题(1.1), (1.2)具有形如(3.2)式的解,其中<span class="formulaText"><inline-formula><tex-math id="M194">$ x(t), w(t) $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M195">$ u_\delta(t) $</tex-math></inline-formula></span>分别由(3.10), (3.11)和(3.12)式给出.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C88">如果<span class="formulaText"><inline-formula><tex-math id="M196">$ m_0 = 0, u_0 = 0 $</tex-math></inline-formula></span>,问题(1.1), (1.2)的解就是黎曼问题(1.1), (2.1)的解,从而反映了我们构造的解关于黎曼初值的小扰动是稳定的.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C89"><strong>情形3.3</strong>   <span class="formulaText"><inline-formula><tex-math id="M197">$ u_0< u_-< u_+ $</tex-math></inline-formula></span> (如果<span class="formulaText"><inline-formula><tex-math id="M198">$ u_-< u_+< u_0 $</tex-math></inline-formula></span>,解的情形是类似的)</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <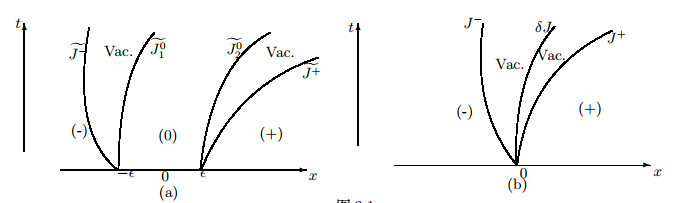p id="C90">在这种情形,当时间<span class="formulaText"><inline-formula><tex-math id="M199">$ t $</tex-math></inline-formula></span>足够小(设<span class="formulaText"><inline-formula><tex-math id="M200">$ t $</tex-math></inline-formula></span>小于某一临界时刻<span class="formulaText"><inline-formula><tex-math id="M201">$ t_1 $</tex-math></inline-formula></span><span class="formulaNumber">)</span>时,问题(1.1), (1.3)的解可表示如下(见<a class="table-icon" style="color:#2150f9" href="#Fig3.4"; id="inline_content图 3.4(a)">图 3.4(a)</a>)</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE19"> $ (\rho_-, u_-e^{-t})+\widetilde{\delta S_{1}}+(\frac{m_0}{2\epsilon}, u_0e^{-t})+\widetilde{J^0}+ Vac.+\widetilde{J^+}+(\rho_+, u_+e^{-t}), $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C91">这里<span class="formulaText"><inline-formula><tex-math id="M202">$ \widetilde{\delta S_{1}} $</tex-math></inline-formula></span>的传播速度为<span class="formulaText"><inline-formula><tex-math id="M203">$ u_\delta ^{1} $</tex-math></inline-formula></span>,其中<span class="formulaText"><inline-formula><tex-math id="M204">$ u_0e^{-t}<u_\delta ^{1} = \sigma_1e^{-t}<u_-e^{-t} $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M205">$ \sigma_1 = \frac{\sqrt{\rho_-}u_-+\sqrt{\frac{m_0}{2\epsilon}} u_0}{\sqrt{\rho_-}+\sqrt{\frac{m_0}{2\epsilon}}} $</tex-math></inline-formula></span><span class="formulaNumber">.</span> <span class="formulaText"><inline-formula><tex-math id="M206">$ \widetilde{J^0} $</tex-math></inline-formula></span>的传播速度为<span class="formulaText"><inline-formula><tex-math id="M207">$ u_0e^{-t} $</tex-math></inline-formula></span><span class="formulaNumber">.</span>因此, <span class="formulaText"><inline-formula><tex-math id="M208">$ \widetilde{\delta S_{1}} $</tex-math></inline-formula></span>将会在<span class="formulaText"><inline-formula><tex-math id="M209">$ t_1 $</tex-math></inline-formula></span>时刻超过<span class="formulaText"><inline-formula><tex-math id="M210">$ \widetilde{J^0} $</tex-math></inline-formula></span>,其交点<span class="formulaText"><inline-formula><tex-math id="M211">$ (x_1, t_1) $</tex-math></inline-formula></span>由下式决定</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE20"> $ \left\{\begin{array}{ll} x_1+\epsilon = \sigma_1(1-e^{-t_1}), \\ x_1-\epsilon = u_0e^{-t_1}, \end{array}\right. $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C92">即</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE21"> $ (x_1, t_1) = \bigg(\frac{\epsilon(\sigma_1+u_0)}{\sigma_1-u_0}, -\ln{(1-\frac{2\epsilon}{\sigma_1-u_0})}\bigg). $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C93">显然,当<span class="formulaText"><inline-formula><tex-math id="M212">$ \epsilon\rightarrow0 $</tex-math></inline-formula></span>时, <span class="formulaText"><inline-formula><tex-math id="M213">$ (x_1, t_1)\rightarrow(0, 0) $</tex-math></inline-formula></span><span class="formulaNumber">.</span></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C94">在<span class="formulaText"><inline-formula><tex-math id="M214">$ t = t_1 $</tex-math></inline-formula></span>时刻,我们将面对方程(1.1)带如下初值的新的初值问题</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.13)</label><tex-math id="E3.13"> $ \begin{equation} (\rho, u)(x, t_1) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t_1}), \ \ \ \ \ \ \ \ \ \ &x<x_1, \\ (\widetilde{w^1}(t_1)\delta(x-x_1), \widetilde{u_\delta^1}(t_1)), \ \ & x = x_1, \\ (0, u_0e^{-t_1}), \ \ \ \ \ \ \ \ \ \ \ \ \ & x_1<x<\epsilon+u_+(1-e^{-t}), \\ (\rho_+, u_+e^{-t_1}), \ \ \ \ \ \ \ \ \ \ \ & x>\epsilon+u_+(1-e^{-t}), \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C95">由情形3.2的分析可知,在<span class="formulaText"><inline-formula><tex-math id="M215">$ t = t_1 $</tex-math></inline-formula></span>之后的短时间内,问题(1.1), (1.3)的解可表示如下</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE22"> $ (\rho_-, u_-e^{-t})+\widetilde{\delta S_{2}}+ Vac.+\widetilde{J^+}+(\rho_+, u_+e^{-t}), $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C96">即</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.14)</label><tex-math id="E3.14"> $ \begin{equation} (\rho, u)(x, t) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t}), \ \ \ \ \ \ \ \ \ \ \ \ \ \ & x<\widetilde{x^2}(t), \\ (\widetilde{w^2}(t)\delta(x-\widetilde{x^2}(t)), \widetilde{u_\delta^2}(t)), \ \ & x = \widetilde{x^2}(t), \\ (0, \widetilde{u}(x, t)), \ \ \ \ \ \ \ \ \ \ \ \ & \widetilde{x^2}(t)<x<\epsilon+u_+(1-e^{-t}), \\ (\rho_+, u_+e^{-t}), \ \ \ \ \ \ \ \ \ \ \ \ \ \ & x>\epsilon+u_+(1-e^{-t}), \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C97">其中<span class="formulaText"><inline-formula><tex-math id="M216">$ x = \widetilde{x^2}(t) $</tex-math></inline-formula></span>代表<span class="formulaText"><inline-formula><tex-math id="M217">$ \widetilde{\delta S_{2}} $</tex-math></inline-formula></span>所在的曲线,且在曲线<span class="formulaText"><inline-formula><tex-math id="M218">$ x = \epsilon+u_\ast(1-e^{-t}) $</tex-math></inline-formula></span>上, <span class="formulaText"><inline-formula><tex-math id="M219">$ \widetilde{u}(x, t) = u_\ast e^{-t} $</tex-math></inline-formula></span>且<span class="formulaText"><inline-formula><tex-math id="M220">$ u_0<u_\ast<u_+ $</tex-math></inline-formula></span>,从而<span class="formulaText"><inline-formula><tex-math id="M221">$ \widetilde{\delta S_{2}} $</tex-math></inline-formula></span>永远不会穿透真空超越<span class="formulaText"><inline-formula><tex-math id="M222">$ \widetilde{J^+} $</tex-math></inline-formula></span><span class="formulaNumber">.</span></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C98">令<span class="formulaText"><inline-formula><tex-math id="M223">$ \epsilon\rightarrow0 $</tex-math></inline-formula></span>时,可得到初值问题(1.1), (1.2)具有如下形式的整体解(见<a class="table-icon" style="color:#2150f9" href="#Fig3.4"; id="inline_content图 3.4(b)">图 3.4(b)</a>)</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.15)</label><tex-math id="E3.15"> $ \begin{equation} (\rho, u)(x, t) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t}), \ \ \ \ \ \ \ \ \ \ \ \ & x<x(t), \\ (w(t)\delta(x-x(t)), u_\delta(t)), \ \ & x = x(t), \\ (0, \bar{u}(x, t)), \ \ \ \ \ \ \ \ \ \ \ & x(t)<x<u_+(1-e^{-t}), \\ (\rho_+, u_+e^{-t}), \ \ \ \ \ \ \ \ \ \ & x>u_+(1-e^{-t}), \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C99">其中,在曲线<span class="formulaText"><inline-formula><tex-math id="M224">$ x = u_\ast(1-e^{-t}) $</tex-math></inline-formula></span>上, <span class="formulaText"><inline-formula><tex-math id="M225">$ \bar{u}(x, t) = u_\ast e^{-t} $</tex-math></inline-formula></span>且<span class="formulaText"><inline-formula><tex-math id="M226">$ u_0<u_\ast<u_+ $</tex-math></inline-formula></span><span class="formulaNumber">.</span>上述解(3.15)满足广义Rankine-Hugoniot条件</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.16)</label><tex-math id="E3.16"> $ \begin{equation} \left\{\begin{array}{ll} \frac{{\rm d}x}{{\rm d}t} = u_\delta, \\ \frac{{\rm d}w}{{\rm d}t} = -\rho_- u_\delta+\rho_- u_-e^{-t}, \\ \frac{{\rm d}(w u_ \delta)}{{\rm d}t}+{w u_ \delta} = -\rho_- u_-u_\delta e^{-t}+\rho_- u_-^2e^{-2t} \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C100">和初值条件</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.17)</label><tex-math id="E3.17"> $ \begin{equation} (x, w, u_\delta)|_{t = 0} = (0, m_0, u_0). \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C101">类似于情形3.2,求解初值问题(3.16), (3.17)可得</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.18)</label><tex-math id="E3.18"> $ \begin{equation} x(t) = \left\{\begin{array}{ll} u_0(1-e^{-t}), \ \ \ \ \ \ \ \ \ \ \ \ \ \ & \rho_- = 0, \\ \frac{-\rho_- u_-(e^{-t}-1)+m_0-w(t)}{\rho_-}, \ \ & \rho_-\neq0, \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.19)</label><tex-math id="E3.19"> $ \begin{equation} w(t) = \{m_0^2+2m_0\rho_-(u_0- u_-)(e^{-t}-1)\}^\frac{1}{2}, \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.20)</label><tex-math id="E3.20"> $ \begin{equation} u_\delta(t) = \frac{1}{w(t)e^t}\{m_0u_0-\rho_- u_-x-\rho_- u_-^2(e^{-t}-1)\}. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <h3 style="position: absolute; opacity: 0; filter:Alpha(opacity=0);">图 3.4</h3> <div class="content-zw-img" id=""> <div class="content-zw-img-img figure outline_anchor" onmouseleave="likai(this);"> <img src="sxwlxb-40-1-49-3.4.jpg" onclick="clickss(this)" onmouseover="huoqukuanduimg(this);" class="tupian"> <p class="tishi"> <a href="sxwlxb-40-1-49-3.4.jpg.html" target="_blank">新窗口打开</a>| <a href="sxwlxb-40-1-49-3.4.jpg.zip">下载原图ZIP</a>| <a href="sxwlxb-40-1-49-3.4.jpg.ppt">生成PPT</a> </p> </div> <div class="content-zw-img-shuoming"> <p class="content-zw-img-shuoming-title-cn"><b>图 3.4   <title/> </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p id="C102">综上可知,在此情形中,初值问题(1.1), (1.2)具有形如(3.15)式的解,其中<span class="formulaText"><inline-formula><tex-math id="M244">$ x(t), w(t) $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M245">$ u_\delta(t) $</tex-math></inline-formula></span>分别由(3.18), (3.19)和(3.20)式给出.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C103">如果<span class="formulaText"><inline-formula><tex-math id="M246">$ m_0 = 0, u_0 = 0 $</tex-math></inline-formula></span>,问题(1.1), (1.2)的解就是黎曼问题(1.1), (2.1)的解,从而反映了我们构造的解关于黎曼初值的小扰动是稳定的.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C104"><strong>情形3.4</strong>   <span class="formulaText"><inline-formula><tex-math id="M247">$ u_0< u_+< u_- $</tex-math></inline-formula></span> (如果<span class="formulaText"><inline-formula><tex-math id="M248">$ u_+< u_-< u_0 $</tex-math></inline-formula></span>,解的情形是类似的)</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C105">由情形3.3的分析可知,对于初值问题(1.1), (1.3),在<span class="formulaText"><inline-formula><tex-math id="M249">$ t>t_1 $</tex-math></inline-formula></span>的短时间内,其解同情形3.3,但是由于此时<span class="formulaText"><inline-formula><tex-math id="M250">$ u_0< u_+< u_- $</tex-math></inline-formula></span>,故<span class="formulaText"><inline-formula><tex-math id="M251">$ u_0e^{-t}< u_+e^{-t}< u_-e^{-t} $</tex-math></inline-formula></span><span class="formulaNumber">.</span>而<span class="formulaText"><inline-formula><tex-math id="M252">$ u_0e^{-t}< \widetilde{u_\delta^2}(t)< u_-e^{-t} $</tex-math></inline-formula></span>,故在某一时刻<span class="formulaText"><inline-formula><tex-math id="M253">$ t = t^\ast>t_1 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M254">$ \widetilde{u_\delta^2}(t^\ast) = u_+e^{-t} $</tex-math></inline-formula></span><span class="formulaNumber">.</span>进一步地,随着时间的发展,在接下来的某一时刻<span class="formulaText"><inline-formula><tex-math id="M255">$ t = t_2>t_\ast $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M256">$ \widetilde{\delta S_{2}} $</tex-math></inline-formula></span>将穿透真空并与<span class="formulaText"><inline-formula><tex-math id="M257">$ \widetilde{J^+} $</tex-math></inline-formula></span>相交,其交点<span class="formulaText"><inline-formula><tex-math id="M258">$ (x_2, t_2) $</tex-math></inline-formula></span>由下式决定</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE23"> $ \left\{\begin{array}{ll} x_2 = \widetilde{x^2}(t_2), \\ x_2-\epsilon = u_+e^{-t_2}. \end{array}\right. $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C106">在<span class="formulaText"><inline-formula><tex-math id="M259">$ t = t_2 $</tex-math></inline-formula></span>时刻,我们将面对(1.1)式带如下初值的新的初值问题</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.21)</label><tex-math id="E3.21"> $ \begin{equation} (\rho, u)(x, t_2) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t_2}), \ \ \ \ \ \ \ \ \ \ \ \ & x<x_2, \\ (\widetilde{w^2}(t_2)\delta(x-x_2), \widetilde{u_\delta^2}(t_2)), \ \ & x = x_2, \\ (\rho_+, u_+e^{-t_2}), \ \ \ \ \ \ \ \ \ \ \ \ & x>x_2, \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C107">其中<span class="formulaText"><inline-formula><tex-math id="M260">$ u_+e^{-t_2}<\widetilde{u_\delta^2}(t_2)<u_-e^{-t_2} $</tex-math></inline-formula></span><span class="formulaNumber">.</span>由情形3.2的分析可知,对于初值问题(1.1), (1.3),当<span class="formulaText"><inline-formula><tex-math id="M261">$ t>t_2 $</tex-math></inline-formula></span>后,解可表示如下(见<a class="table-icon" style="color:#2150f9" href="#Fig3.5"; id="inline_content图 3.5(a)">图 3.5(a)</a>)</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label/><tex-math id="FE24"> $ (\rho_-, u_-e^{-t})+\widetilde{\delta S_{3}}+(\rho_+, u_+e^{-t}). $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C108">令<span class="formulaText"><inline-formula><tex-math id="M262">$ \epsilon\rightarrow0 $</tex-math></inline-formula></span>时,记<span class="formulaText"><inline-formula><tex-math id="M263">$ \lim\limits_{\epsilon\rightarrow0}(x_2, t_2) = (\overline{x}, \overline{t}) $</tex-math></inline-formula></span>,可得到初值问题(1.1), (1.2)具有如下形式的整体解(见<a class="table-icon" style="color:#2150f9" href="#Fig3.5"; id="inline_content图 3.5(b)">图 3.5(b)</a>).</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C109">当<span class="formulaText"><inline-formula><tex-math id="M264">$ t\leq \overline{t} $</tex-math></inline-formula></span>,解同情形3.3,即</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.22)</label><tex-math id="E3.22"> $ \begin{equation} (\rho, u)(x, t) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t}), \ \ \ \ \ \ \ \ \ \ \ \ \ \ & x<x^1(t), \\ (w^1(t)\delta(x-x^1(t)), u_\delta^1(t)), \ \ & x = x^1(t), \\ (0, \bar{u}(x, t)), \ \ \ \ \ \ \ \ \ \ \ \ \ \ & x^1(t)<x<u_+(1-e^{-t}), \\ (\rho_+, u_+e^{-t}), \ \ \ \ \ \ \ \ \ \ \ \ \ & x>u_+(1-e^{-t}), \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C110">其中<span class="formulaText"><inline-formula><tex-math id="M265">$ x^1(t), w^1(t), u_\delta^1(t) $</tex-math></inline-formula></span>分别由(3.18), (3.19)和(3.20)式给出,且在曲线<span class="formulaText"><inline-formula><tex-math id="M266">$ x = u_\ast(1-e^{-t}) $</tex-math></inline-formula></span>上, <span class="formulaText"><inline-formula><tex-math id="M267">$ \bar{u}(x, t) = u_\ast e^{-t} $</tex-math></inline-formula></span>且<span class="formulaText"><inline-formula><tex-math id="M268">$ u_0<u_\ast<u_\delta^1(\overline{t}) $</tex-math></inline-formula></span><span class="formulaNumber">.</span></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C111">当<span class="formulaText"><inline-formula><tex-math id="M269">$ t\geq \overline{t} $</tex-math></inline-formula></span>时,解为</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.23)</label><tex-math id="E3.23"> $ \begin{equation} (\rho, u)(x, t) = \left\{\begin{array}{ll} (\rho_-, u_-e^{-t}), \ \ \ \ \ \ \ \ \ \ \ & x<x^2(t), \\ (w^2(t)\delta(x-x^2(t)), u_\delta^2(t)), \ \ & x = x^2(t), \\ (\rho_+, u_+e^{-t}), \ \ \ \ \ \ \ \ \ \ \ \ & x>x^2(t). \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C112">其中<span class="formulaText"><inline-formula><tex-math id="M270">$ (x^2(t), w^2(t), u_\delta^2(t)) $</tex-math></inline-formula></span>由广义Rankine-Hugoniot条件</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.24)</label><tex-math id="E3.24"> $ \begin{equation} \left\{\begin{array}{ll} \frac{{\rm d}x^2}{{\rm d}t} = u_\delta^2, \\ \frac{{\rm d}w^2}{{\rm d}t} = [\rho] u_\delta^2-[\rho u]e^{-t}, \\ \frac{{\rm d}(w^2 u_ \delta^2)}{{\rm d}t}+{w^2 u_ \delta^2} = [\rho u] u_\delta^2 e^{-t}-[\rho u^2]e^{-2t} \end{array}\right. \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C113">和初值条件</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p><disp-formula><label>(3.25)</label><tex-math id="E3.25"> $ \begin{equation} (x^2, w^2, u_\delta^2)|_{t = \overline{t}} = (\overline{x}, w^1(\overline{t}), u_\delta^1(\overline{t})) \end{equation} $ </tex-math></disp-formula></p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C114">唯一确定,这里<span class="formulaText"><inline-formula><tex-math id="M271">$ [\rho] = \rho_+-\rho_- $</tex-math></inline-formula></span><span class="formulaNumber">.</span></p> </div> </div> <h3 style="position: absolute; opacity: 0; filter:Alpha(opacity=0);">图 3.5</h3> <div class="content-zw-img" id=""> <div class="content-zw-img-img figure outline_anchor" onmouseleave="likai(this);"> <img src="sxwlxb-40-1-49-3.5.jpg" onclick="clickss(this)" onmouseover="huoqukuanduimg(this);" class="tupian"> <p class="tishi"> <a href="sxwlxb-40-1-49-3.5.jpg.html" target="_blank">新窗口打开</a>| <a href="sxwlxb-40-1-49-3.5.jpg.zip">下载原图ZIP</a>| <a href="sxwlxb-40-1-49-3.5.jpg.ppt">生成PPT</a> </p> </div> <div class="content-zw-img-shuoming"> <p class="content-zw-img-shuoming-title-cn"><b>图 3.5   <title/> </b></p> </div> </div> <br> <div class="paragraph"> <div class="content-zw-1"> <p id="C115">如果<span class="formulaText"><inline-formula><tex-math id="M291">$ m_0 = 0, u_0 = 0 $</tex-math></inline-formula></span>,问题(1.1), (1.2)的解就是黎曼问题(1.1), (2.1)的解,从而反映了我们构造的解关于黎曼初值的小扰动是稳定的.</p> </div> </div> <h2 class="title-biaoti outline_anchor" level="1" id="outline_anchor_1"> 4 结论 </h2> <div class="paragraph"> <div class="content-zw-1"> <p id="C116">综合第三部分结果,我们可以得到关于初值含<span class="formulaText"><inline-formula><tex-math id="M292">$ \delta $</tex-math></inline-formula></span> -函数的初值问题(1.1), (1.2)的如下结论.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C117"><strong>定理4.1</strong>  对于初值问题(1.1), (1.2),如果<span class="formulaText"><inline-formula><tex-math id="M293">$ u_-\leq u_0\leq u_+ $</tex-math></inline-formula></span>,解由接触间断、真空、<span class="formulaText"><inline-formula><tex-math id="M294">$ \delta $</tex-math></inline-formula></span> -接触间断、真空和接触间断构成;如果<span class="formulaText"><inline-formula><tex-math id="M295">$ u_+< u_0<u_- $</tex-math></inline-formula></span>,解由<span class="formulaText"><inline-formula><tex-math id="M296">$ \delta $</tex-math></inline-formula></span> -激波构成;如果<span class="formulaText"><inline-formula><tex-math id="M297">$ u_0< u_-< u_+(u_-< u_+< u_0) $</tex-math></inline-formula></span>,解由<span class="formulaText"><inline-formula><tex-math id="M298">$ \delta $</tex-math></inline-formula></span> -激波、真空和接触间断构成;如果<span class="formulaText"><inline-formula><tex-math id="M299">$ u_0< u_+< u_-(u_+< u_-< u_0) $</tex-math></inline-formula></span>,前期解由<span class="formulaText"><inline-formula><tex-math id="M300">$ \delta $</tex-math></inline-formula></span> -激波、真空和接触间断构成,后期解由<span class="formulaText"><inline-formula><tex-math id="M301">$ \delta $</tex-math></inline-formula></span> -激波构成.</p> </div> </div> <div class="paragraph"> <div class="content-zw-1"> <p id="C118">本文的结果给出了研究初始波包含<span class="formulaText"><inline-formula><tex-math id="M302">$ \delta $</tex-math></inline-formula></span> -激波的波的相互作用的一种方法,后期我们将会继续开展该方面的研究.另外,我们还将在本文的基础上考虑二维甚至一般高维的带群集耗散项的零压流方程组的黎曼问题,这将是对高维非齐次守恒律组的一个基础性探索.</p> </div> </div> <div class="cankaowenxian1"></div> <h2 class="title-biaoti"> <span class="outline_anchor" level="1">参考文献 </span> <div class="btn-group"> <button style="font-size:11px;padding:3px;" type="button" onclick="sddas();" class="btn btn-info dropdown-toggle" data-toggle="dropdown"> View Option <span class="caret"></span> </button> <ul class="dropdown-menu kkaqqqq" role="menu" style="background:#e1e7ea;padding-left:0px !important;"> <li onclick="daxcbdh();"><a href="javascript:;" class="ref_sort" type="1" style="color:#000;">原文顺序</a></li> <li onclick="daxcbdh();"><a href="javascript:;" class="ref_sort" type="2" style="color:#000;">文献年度倒序</a></li> <li onclick="daxcbdh();"><a href="javascript:;" class="ref_sort" type="3" style="color:#000;">文中引用次数倒序</a></li> <li onclick="daxcbdh();"><a href="javascript:;" class="ref_sort" type="4" style="color:#000;">被引期刊影响因子</a></li> </ul> </div> </h2> <div class="cankaowenxian"> <div id="b1" name="b1" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [1] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="data" xml:lang="en">Bouchut F. On Zero-pressure Gas Dynamics//Perthame B, et al. Advances in Kinetic Theory and Computing: Adv Math Appl Sci. Sinapore: World Scientific, 1994: 171-190</mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8281"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b1')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b2" name="b2" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [2] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Brenier</surname> <given-names>Y</given-names> </name>, <name> <surname>Gangbo</surname> <given-names>W</given-names> </name>, <name> <surname>Savare</surname> <given-names>G</given-names> </name>, <name> <surname>Westdickenberg</surname> <given-names>M</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The sticky particles dynamicse with interactions</p><source>J Math Pures Appl</source>, <year>2013</year>, <volume><strong>99</strong></volume>, <fpage>577</fpage>- <lpage>617</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="https://www.sciencedirect.com/science/article/pii/S0034487710000145" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8282"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b2')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b3" name="b3" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [3] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Danilvo</surname> <given-names>V G</given-names> </name>, <name> <surname>Shelkovich</surname> <given-names>V M</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Dynamics of propagation and interaction of δ-shock waves in conservation law system</p><source>J Differential Equations</source>, <year>2005</year>, <volume><strong>221</strong></volume>, <fpage>333</fpage>- <lpage>381</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8283"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b3')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b4" name="b4" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [4] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Danilvo</surname> <given-names>V G</given-names> </name>, <name> <surname>Shelkovich</surname> <given-names>V M</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Delta-shock waves type solution of hyperbolic systems of conservation laws</p><source>Q Appl Math</source>, <year>2005</year>, <volume><strong>63</strong></volume>, <fpage>401</fpage>- <lpage>427</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8284"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b4')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b5" name="b5" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [5] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Ding</surname> <given-names>Y</given-names> </name>, <name> <surname>Huang</surname> <given-names>F M</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">On a nonhomogeneous system of pressureless flow</p><source>Quart Appl Math</source>, <year>2002</year>, <volume><strong>62</strong></volume> (<issue>3</issue>): <fpage>509</fpage>- <lpage>528</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e9ee6df49c139693b2c3a770c97e4cc6" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8285"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b5')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b6" name="b6" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [6] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>E</surname> <given-names>W</given-names> </name>, <name> <surname>Rykov</surname> <given-names>Yu G</given-names> </name>, <name> <surname>Sinai</surname> <given-names>Ya G</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Generalized varinational principles, global weak solutions and behavior with random initial data for systems of conservation laws arising in adhesion particle dynamics</p><source>Comm Math Phys</source>, <year>1996</year>, <volume><strong>177</strong></volume>, <fpage>349</fpage>- <lpage>380</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="https://web.math.princeton.edu/~weinan/pdf%20files/generalized%20variational.pdf" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8286"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b6')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b7" name="b7" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [7] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Guo</surname> <given-names>L</given-names> </name>, <name> <surname>Li</surname> <given-names>T</given-names> </name>, <name> <surname>Pan</surname> <given-names>L</given-names> </name>, <name> <surname>Han</surname> <given-names>X</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The Riemann with delta inital data for the one-dimensional Chaplygin gas equations with a source term</p><source>Nonlinear Anal:Real Word Appl</source>, <year>2018</year>, <volume><strong>41</strong></volume>, <fpage>588</fpage>- <lpage>606</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="https://www.sciencedirect.com/science/article/pii/S0252960212600642" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8287"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b7')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b8" name="b8" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [8] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Ha</surname> <given-names>S Y</given-names> </name>, <name> <surname>Huang</surname> <given-names>F</given-names> </name>, <name> <surname>Wang</surname> <given-names>Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">A global unique solvability of entropic weak solution to the one-dimensional pressureless Euler system with a flocking dissipation</p><source>J Differential Equations</source>, <year>2014</year>, <volume><strong>2257</strong></volume>, <fpage>1333</fpage>- <lpage>1371</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f1e1b3d4ccc184178e5227fa63daa9c7" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8288"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b8')" class="bianju"> [本文引用: 4]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b9" name="b9" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [9] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Ha</surname> <given-names>S Y</given-names> </name>, <name> <surname>Liu</surname> <given-names>J G</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">A simple proof of the cucker-smale flocking dynamics and mean-field limit</p><source>Commun Math Sci</source>, <year>2009</year>, <volume><strong>7</strong></volume> (<issue>2</issue>): <fpage>297</fpage>- <lpage>325</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=0e756a748c8a467ef69d1413dea794ea" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8289"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b9')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b10" name="b10" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [10] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Huang</surname> <given-names>F</given-names> </name>, <name> <surname>Wang</surname> <given-names>Z</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Well posedness for pressureless flow</p><source>Comm Math Phys</source>, <year>2001</year>, <volume><strong>222</strong></volume>, <fpage>117</fpage>- <lpage>146</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=79f6b53cdf0db40c0929a2e96978faa2" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8290"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b10')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b11" name="b11" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [11] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Jin</surname> <given-names>C Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Well posedness for pressureless Euler system with a flocking dissipation in Wasserstein space</p><source>Nonlinear Anal TMA</source>, <year>2015</year>, <volume><strong>128</strong></volume>, <fpage>412</fpage>- <lpage>422</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=3796bb7a0a00fbaf3b9478ce418fa394" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8291"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b11')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b12" name="b12" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [12] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Jin</surname> <given-names>C Y</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Existence and uniqueness of entropy solution to pressureless Euler system with a flocking dissipation</p><source>Acta Mathematica Scientia</source>, <year>2016</year>, <volume><strong>36B</strong></volume> (<issue>5</issue>): <fpage>1262</fpage>- <lpage>1284</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sxwlxb-e201605003" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8292"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b12')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b13" name="b13" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [13] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Kalisch</surname> <given-names>H</given-names> </name>, <name> <surname>Mitrovic</surname> <given-names>D</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Singular solutions of a fully nonlinear 2×2 system of conservation laws</p><source>Proceedings of the Edinburgh Mathematical Society</source>, <year>2012</year>, <volume><strong>55</strong></volume>, <fpage>711</fpage>- <lpage>729</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=PEM2_55_03\PEM\PEM2_55_03\S0013091512000065h.xml" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8293"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b13')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b14" name="b14" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [14] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Kalisch</surname> <given-names>H</given-names> </name>, <name> <surname>Mitrovic</surname> <given-names>D</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Singular solutions for shallow water equations</p><source>IMA J Appl Math</source>, <year>2012</year>, <volume><strong>77</strong></volume>, <fpage>340</fpage>- <lpage>350</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8294"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b14')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b15" name="b15" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [15] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="data" xml:lang="en">Li J, Zhang T, Yang S. The Two-dimensional Riemann Prolem in Gas Dynamics. Pitman Monogr Surv Pure Appl Math. Harlow: Longman Scientific and Technical, 1998</mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8295"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b15')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b16" name="b16" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [16] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Nedeljkov</surname> <given-names>M</given-names> </name>, <name> <surname>Oberguggenberger</surname> <given-names>M</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Interactions of delta shock waves in a strictly hyperbolic system of conservation laws</p><source>J Math Anal Appl</source>, <year>2008</year>, <volume><strong>344</strong></volume>, <fpage>1143</fpage>- <lpage>1157</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://cn.bing.com/academic/profile?id=4c69197f3981a69c4c5fb3d7e81dcacd&encoded=0&v=paper_preview&mkt=zh-cn" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8296"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b16')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b17" name="b17" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [17] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Shen</surname> <given-names>C</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The Riemann problem for the pressureless Euler system with the Coulomb-like friction term</p><source>IAM J Appl Math</source>, <year>2016</year>, <volume><strong>81</strong></volume>, <fpage>76</fpage>- <lpage>99</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=1128bb0814121310368c8b5f0637a918" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8297"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b17')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b18" name="b18" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [18] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Shen</surname> <given-names>C</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The Riemann problem for the Chaplygin gas equations with a source term</p><source>Z Angew Math Mech</source>, <year>1999</year>, <volume><strong>96</strong></volume>, <fpage>681</fpage>- <lpage>695</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://cn.bing.com/academic/profile?id=a99e097148f6ed0c288452d9aab68808&encoded=0&v=paper_preview&mkt=zh-cn" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8298"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b18')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b19" name="b19" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [19] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Shen</surname> <given-names>C</given-names> </name>, <name> <surname>Sun</surname> <given-names>M</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Interactions of delta shocks for transport equations with split delta functions</p><source>J Math Anal Appl</source>, <year>2009</year>, <volume><strong>351</strong></volume>, <fpage>747</fpage>- <lpage>755</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8299"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b19')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b20" name="b20" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [20] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="data" xml:lang="en">Sheng W, Zhang T. The Riemann Problem for Transportation Equations in Gas Dynamics. Providence, RI: Mem Amer Math Soc, 1999</mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8300"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b20')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b21" name="b21" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [21] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Sun</surname> <given-names>M</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The exact Riemann solutions to the generalized Chaplygin gas equations with friction</p><source>Commun Nonlinear Sci Numer Simulat</source>, <year>2016</year>, <volume><strong>36</strong></volume>, <fpage>342</fpage>- <lpage>353</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=b1ea89818dee63096213fb2f7cb27d57" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8301"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b21')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b22" name="b22" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [22] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Wang</surname> <given-names>L</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The Riemann problem with delta data for zero-pressure gas dynamcis</p><source>Chinese Annals of Mathematics</source>, <year>2016</year>, <volume><strong>37</strong></volume> (<issue>3</issue>): <fpage>441</fpage>- <lpage>450</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="https://link.springer.com/article/10.1007/s11401-016-0962-8" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8302"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b22')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b23" name="b23" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [23] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Wang</surname> <given-names>Z</given-names> </name>, <name> <surname>Ding</surname> <given-names>X</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Uniqueness of generalized solution for the Cauchy problem of transportation equations</p><source>Acta Math Scientia</source>, <year>1997</year>, <volume><strong>17</strong></volume> (<issue>3</issue>): <fpage>341</fpage>- <lpage>352</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://cn.bing.com/academic/profile?id=4ef1ba9189421a6d4d08e1d7fec00ff1&encoded=0&v=paper_preview&mkt=zh-cn" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8303"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b23')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b24" name="b24" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [24] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Wang</surname> <given-names>Z</given-names> </name>, <name> <surname>Huang</surname> <given-names>F</given-names> </name>, <name> <surname>Ding</surname> <given-names>X</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">On the Cauchy problem of transportation equations</p><source>Acta Math Appl Sinica</source>, <year>1997</year>, <volume><strong>13</strong></volume> (<issue>2</issue>): <fpage>113</fpage>- <lpage>122</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://d.old.wanfangdata.com.cn/NSTLQK/10.1007-BF02015132/" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8304"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b24')" class="bianju"> [本文引用: 3]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b25" name="b25" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [25] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Wang</surname> <given-names>Z</given-names> </name>, <name> <surname>Zhang</surname> <given-names>Q</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The Riemann problem with delta initial data for the one-dimensional Chaplygin gas equations</p><source>Acta Mathematica Scientia</source>, <year>2012</year>, <volume><strong>32B</strong></volume> (<issue>3</issue>): <fpage>825</fpage>- <lpage>841</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://cn.bing.com/academic/profile?id=97678e6182f870676978bdcc2f88abd9&encoded=0&v=paper_preview&mkt=zh-cn" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8305"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b25')" class="bianju"> [本文引用: 2]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b26" name="b26" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [26] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Yang</surname> <given-names>H</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">Generalized plane delta-shock waves for n-dimensional zero-pressure gas dynamics</p><source>J Math Anal Appl</source>, <year>2001</year>, <volume><strong>260</strong></volume>, <fpage>18</fpage>- <lpage>35</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dfce7624c950386d4e341dd33750648d" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> </p> <div class="xiangxicankao"> <p> </p> </div> </div> <div id="b27" name="b27" magrefid="" class="cankaowenxian-xx"> <label class="lableq"> [27] </label> <div class="cankaowenxian-xx-title"> <mixed-citation publication-type="journal"> <person-group person-group-type="author"> <name> <surname>Yang</surname> <given-names>H</given-names> </name>, <name> <surname>Sun</surname> <given-names>W</given-names> </name>. </person-group> <p class="cankaowenxian-xx-z">The Riemann problem with delta initial data for a class of coupled hyperbolic system of conservation laws</p><source>Nonlinear Anal</source>, <year>2007</year>, <volume><strong>67</strong></volume>, <fpage>3041</fpage>- <lpage>3049</lpage> </mixed-citation> </div> <p class="cankaowenxian-xx-x" id="linked_"> <span class="jcr_"></span> <span class="cjcr_"></span> <a href="http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a0e2ad19a28ddf4dc6a7305d31bcb002" target="_blank">URL</a>     <span class="cited" id="bd_cited_count_"></span> <span class="cited" id="cited_8307"> <a href="javascript:;" onmouseover="jjaxxawwhah1(this,'b27')" class="bianju"> [本文引用: 1]</a> </span> </p> <div class="xiangxicankao"> <p> </p> </div> <div> <div id="article_reference_meta" style="display: none;"> <div id="article_reference_meta_b1"> <div id="article_reference_meta_b1_title" class="title_"></div> <div id="article_reference_meta_b1_citedNumber">2</div> <div id="article_reference_meta_b1_nian"></div> <div id="article_reference_meta_b1_jcr"></div> <div id="article_reference_meta_b1_cjcr"></div> <div id="article_reference_meta_b1_articleCitedText"> <div class="sentence">... 当(1.1)式右端的非齐次项为零时,它就是人们常见的零压流模型(输运方程).该模型是研究狄拉克激波(<span class="formulaText"><inline-formula><tex-math id="M5">$ \delta $</tex-math></inline-formula></span> -激波)和真空形成的最重要模型.自1994年起,它便被人们广泛研究,见文献[<xref ref-type="bibr" rid="b1">1</xref>, <xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b20">20</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]等.特别地, Bouchut首次给出了其黎曼问题测度解的存在性<sup>[<xref ref-type="bibr" rid="b1">1</xref>]</sup>,丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... [<xref ref-type="bibr" rid="b1">1</xref>]</sup>,丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> </div> </div> <div id="article_reference_meta_b2"> <div id="article_reference_meta_b2_title" class="title_">The sticky particles dynamicse with interactions</div> <div id="article_reference_meta_b2_citedNumber">1</div> <div id="article_reference_meta_b2_nian">2013</div> <div id="article_reference_meta_b2_jcr"></div> <div id="article_reference_meta_b2_cjcr"></div> <div id="article_reference_meta_b2_articleCitedText"> <div class="sentence">... 证明了其初值为可测函数时柯西问题弱解的存在性和唯一性.紧接着,在文献[<xref ref-type="bibr" rid="b10">10</xref>]中,黄飞敏和王振又将结果推广到初值为Radon测度的情形.此后,对于含各种形式非齐次项的零压流方程陆续有了相关研究结果<sup>[<xref ref-type="bibr" rid="b2">2</xref>, <xref ref-type="bibr" rid="b5">5</xref>, <xref ref-type="bibr" rid="b17">17</xref>]</sup>.在这些文献的基础上,本文给出了初值问题(1.1)–(1.2)弱解的存在性,唯一性和大时间渐近行为等方面新的结果.在后面的研究中,作者还将在本文研究基础上进一步考虑含间断非齐次项的零压流的初值问题. ...</div> </div> </div> <div id="article_reference_meta_b3"> <div id="article_reference_meta_b3_title" class="title_">Dynamics of propagation and interaction of δ-shock waves in conservation law system</div> <div id="article_reference_meta_b3_citedNumber">1</div> <div id="article_reference_meta_b3_nian">2005</div> <div id="article_reference_meta_b3_jcr"></div> <div id="article_reference_meta_b3_cjcr"></div> <div id="article_reference_meta_b3_articleCitedText"> <div class="sentence">... 为方便起见,我们选择参数<span class="formulaText"><inline-formula><tex-math id="M60">$ s = t $</tex-math></inline-formula></span>,并用<span class="formulaText"><inline-formula><tex-math id="M61">$ w(t) = \sqrt{1+{x'(t)}^2}p(t) $</tex-math></inline-formula></span>来表示<span class="formulaText"><inline-formula><tex-math id="M62">$ \delta $</tex-math></inline-formula></span> -激波的强度(质量).接下来,我们将给出黎曼问题(1.1), (2.1)的<span class="formulaText"><inline-formula><tex-math id="M63">$ \delta $</tex-math></inline-formula></span> -激波解的定义.该定义框架由Danilov和Shelkovich<sup>[<xref ref-type="bibr" rid="b3">3</xref>-<xref ref-type="bibr" rid="b4">4</xref>]</sup>提出,并经Kalisch和Mitrovic<sup>[<xref ref-type="bibr" rid="b13">13</xref>-<xref ref-type="bibr" rid="b14">14</xref>]</sup>发展而来. ...</div> </div> </div> <div id="article_reference_meta_b4"> <div id="article_reference_meta_b4_title" class="title_">Delta-shock waves type solution of hyperbolic systems of conservation laws</div> <div id="article_reference_meta_b4_citedNumber">1</div> <div id="article_reference_meta_b4_nian">2005</div> <div id="article_reference_meta_b4_jcr"></div> <div id="article_reference_meta_b4_cjcr"></div> <div id="article_reference_meta_b4_articleCitedText"> <div class="sentence">... 为方便起见,我们选择参数<span class="formulaText"><inline-formula><tex-math id="M60">$ s = t $</tex-math></inline-formula></span>,并用<span class="formulaText"><inline-formula><tex-math id="M61">$ w(t) = \sqrt{1+{x'(t)}^2}p(t) $</tex-math></inline-formula></span>来表示<span class="formulaText"><inline-formula><tex-math id="M62">$ \delta $</tex-math></inline-formula></span> -激波的强度(质量).接下来,我们将给出黎曼问题(1.1), (2.1)的<span class="formulaText"><inline-formula><tex-math id="M63">$ \delta $</tex-math></inline-formula></span> -激波解的定义.该定义框架由Danilov和Shelkovich<sup>[<xref ref-type="bibr" rid="b3">3</xref>-<xref ref-type="bibr" rid="b4">4</xref>]</sup>提出,并经Kalisch和Mitrovic<sup>[<xref ref-type="bibr" rid="b13">13</xref>-<xref ref-type="bibr" rid="b14">14</xref>]</sup>发展而来. ...</div> </div> </div> <div id="article_reference_meta_b5"> <div id="article_reference_meta_b5_title" class="title_">On a nonhomogeneous system of pressureless flow</div> <div id="article_reference_meta_b5_citedNumber">1</div> <div id="article_reference_meta_b5_nian">2002</div> <div id="article_reference_meta_b5_jcr"></div> <div id="article_reference_meta_b5_cjcr"></div> <div id="article_reference_meta_b5_articleCitedText"> <div class="sentence">... 证明了其初值为可测函数时柯西问题弱解的存在性和唯一性.紧接着,在文献[<xref ref-type="bibr" rid="b10">10</xref>]中,黄飞敏和王振又将结果推广到初值为Radon测度的情形.此后,对于含各种形式非齐次项的零压流方程陆续有了相关研究结果<sup>[<xref ref-type="bibr" rid="b2">2</xref>, <xref ref-type="bibr" rid="b5">5</xref>, <xref ref-type="bibr" rid="b17">17</xref>]</sup>.在这些文献的基础上,本文给出了初值问题(1.1)–(1.2)弱解的存在性,唯一性和大时间渐近行为等方面新的结果.在后面的研究中,作者还将在本文研究基础上进一步考虑含间断非齐次项的零压流的初值问题. ...</div> </div> </div> <div id="article_reference_meta_b6"> <div id="article_reference_meta_b6_title" class="title_">Generalized varinational principles, global weak solutions and behavior with random initial data for systems of conservation laws arising in adhesion particle dynamics</div> <div id="article_reference_meta_b6_citedNumber">2</div> <div id="article_reference_meta_b6_nian">1996</div> <div id="article_reference_meta_b6_jcr"></div> <div id="article_reference_meta_b6_cjcr"></div> <div id="article_reference_meta_b6_articleCitedText"> <div class="sentence">... 当(1.1)式右端的非齐次项为零时,它就是人们常见的零压流模型(输运方程).该模型是研究狄拉克激波(<span class="formulaText"><inline-formula><tex-math id="M5">$ \delta $</tex-math></inline-formula></span> -激波)和真空形成的最重要模型.自1994年起,它便被人们广泛研究,见文献[<xref ref-type="bibr" rid="b1">1</xref>, <xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b20">20</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]等.特别地, Bouchut首次给出了其黎曼问题测度解的存在性<sup>[<xref ref-type="bibr" rid="b1">1</xref>]</sup>,丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M19">$ \delta $</tex-math></inline-formula></span>是标准的狄拉克函数, <span class="formulaText"><inline-formula><tex-math id="M20">$ m_0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M21">$ u_0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M22">$ \rho_\pm $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M23">$ u_\pm $</tex-math></inline-formula></span>是任意常数.因为模型(1.1)的黎曼解中出现了<span class="formulaText"><inline-formula><tex-math id="M24">$ \delta $</tex-math></inline-formula></span> -激波,很自然地我们要考虑其初值含<span class="formulaText"><inline-formula><tex-math id="M25">$ \delta $</tex-math></inline-formula></span> -测度的初值问题(1.2).对于零压流、Chaplygin气体方程和其他方程类似初值问题的研究,可参考文献[<xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b25">25</xref>-<xref ref-type="bibr" rid="b27">27</xref>]. ...</div> </div> </div> <div id="article_reference_meta_b7"> <div id="article_reference_meta_b7_title" class="title_">The Riemann with delta inital data for the one-dimensional Chaplygin gas equations with a source term</div> <div id="article_reference_meta_b7_citedNumber">1</div> <div id="article_reference_meta_b7_nian">2018</div> <div id="article_reference_meta_b7_jcr"></div> <div id="article_reference_meta_b7_cjcr"></div> <div id="article_reference_meta_b7_articleCitedText"> <div class="sentence">... 接下来,令<span class="formulaText"><inline-formula><tex-math id="M31">$ \epsilon\rightarrow0 $</tex-math></inline-formula></span>,由弱解的稳定性理论,并结合广义Rankine-Hugoniot条件和广义熵条件,我们构造性地得到了模型(1.1)–(1.2)的唯一整体解.而且,其解中也包含了<span class="formulaText"><inline-formula><tex-math id="M32">$ \delta $</tex-math></inline-formula></span> -接触间断.进一步地,取<span class="formulaText"><inline-formula><tex-math id="M33">$ m_{0} = 0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M34">$ u_{0} = 0 $</tex-math></inline-formula></span>,模型(1.1)–(1.2)的解正好对应于(1.1)的黎曼解.在文献[<xref ref-type="bibr" rid="b25">25</xref>]中,作者和其导师首次应用本文中构造解的方法成功解决了一维Chaplygin气体初值含<span class="formulaText"><inline-formula><tex-math id="M35">$ \delta $</tex-math></inline-formula></span> -函数的初值问题.近年来,该方法已经被应用于研究很多相关方程组的类似问题<sup>[<xref ref-type="bibr" rid="b7">7</xref>, <xref ref-type="bibr" rid="b22">22</xref>]</sup>. ...</div> </div> </div> <div id="article_reference_meta_b8"> <div id="article_reference_meta_b8_title" class="title_">A global unique solvability of entropic weak solution to the one-dimensional pressureless Euler system with a flocking dissipation</div> <div id="article_reference_meta_b8_citedNumber">4</div> <div id="article_reference_meta_b8_nian">2014</div> <div id="article_reference_meta_b8_jcr"></div> <div id="article_reference_meta_b8_cjcr"></div> <div id="article_reference_meta_b8_articleCitedText"> <div class="sentence">... 模型(1.1)是群体运动模型Cucker-Smale模型趋于平衡态时的动力学描述,其详细推导可参考文献[<xref ref-type="bibr" rid="b8">8</xref>].目前已经得到关于该模型的一些适定性结果<sup>[<xref ref-type="bibr" rid="b8">8</xref>, <xref ref-type="bibr" rid="b11">11</xref>-<xref ref-type="bibr" rid="b12">12</xref>]</sup>. Cucker-Smale模型是描述群体现象的一个离散模型,其动力学方面的研究近年来受到了广泛关注,比如文献[<xref ref-type="bibr" rid="b9">9</xref>]中关于渐近行为和稳定性的研究. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... [<xref ref-type="bibr" rid="b8">8</xref>, <xref ref-type="bibr" rid="b11">11</xref>-<xref ref-type="bibr" rid="b12">12</xref>]</sup>. Cucker-Smale模型是描述群体现象的一个离散模型,其动力学方面的研究近年来受到了广泛关注,比如文献[<xref ref-type="bibr" rid="b9">9</xref>]中关于渐近行为和稳定性的研究. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 对于模型(1.1), Ha,黄飞敏和王益等在2014年首次推导出了该模型,并通过引入广义势得到了当初值<span class="formulaText"><inline-formula><tex-math id="M8">$ \rho_{0}\in L_{loc}^{1}({\Bbb R}) $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M9">$ u_{0}\in L^{\infty}({\Bbb R}) $</tex-math></inline-formula></span>时其整体熵解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b8">8</xref>]</sup>.随后,金春银将他们的结果推广到<span class="formulaText"><inline-formula><tex-math id="M11">$ \rho_{0} $</tex-math></inline-formula></span>是Radon测度, <span class="formulaText"><inline-formula><tex-math id="M12">$ u_{0}\in L^{\infty}(\rho_{0}) $</tex-math></inline-formula></span>的情形<sup>[<xref ref-type="bibr" rid="b12">12</xref>]</sup>,并得到了该模型在Wasserstein空间的适定性<sup>[<xref ref-type="bibr" rid="b11">11</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 对于模型(1.1)的黎曼问题,我们知道<span class="formulaText"><inline-formula><tex-math id="M15">$ \delta $</tex-math></inline-formula></span> -激波和真空确实会出现<sup>[<xref ref-type="bibr" rid="b8">8</xref>, <xref ref-type="bibr" rid="b11">11</xref>]</sup>.另外,基本波的相互作用在理论、数值计算和应用方面都起着很重要的作用.因此,本文中我们主要研究模型(1.1)初值含<span class="formulaText"><inline-formula><tex-math id="M17">$ \delta $</tex-math></inline-formula></span> -测度的扰动黎曼问题和包含<span class="formulaText"><inline-formula><tex-math id="M18">$ \delta $</tex-math></inline-formula></span> -激波和真空的所有可能的波的相互作用,即我们重点关注模型(1.1)的如下初值问题 ...</div> </div> </div> <div id="article_reference_meta_b9"> <div id="article_reference_meta_b9_title" class="title_">A simple proof of the cucker-smale flocking dynamics and mean-field limit</div> <div id="article_reference_meta_b9_citedNumber">1</div> <div id="article_reference_meta_b9_nian">2009</div> <div id="article_reference_meta_b9_jcr"></div> <div id="article_reference_meta_b9_cjcr"></div> <div id="article_reference_meta_b9_articleCitedText"> <div class="sentence">... 模型(1.1)是群体运动模型Cucker-Smale模型趋于平衡态时的动力学描述,其详细推导可参考文献[<xref ref-type="bibr" rid="b8">8</xref>].目前已经得到关于该模型的一些适定性结果<sup>[<xref ref-type="bibr" rid="b8">8</xref>, <xref ref-type="bibr" rid="b11">11</xref>-<xref ref-type="bibr" rid="b12">12</xref>]</sup>. Cucker-Smale模型是描述群体现象的一个离散模型,其动力学方面的研究近年来受到了广泛关注,比如文献[<xref ref-type="bibr" rid="b9">9</xref>]中关于渐近行为和稳定性的研究. ...</div> </div> </div> <div id="article_reference_meta_b10"> <div id="article_reference_meta_b10_title" class="title_">Well posedness for pressureless flow</div> <div id="article_reference_meta_b10_citedNumber">3</div> <div id="article_reference_meta_b10_nian">2001</div> <div id="article_reference_meta_b10_jcr"></div> <div id="article_reference_meta_b10_cjcr"></div> <div id="article_reference_meta_b10_articleCitedText"> <div class="sentence">... 当(1.1)式右端的非齐次项为零时,它就是人们常见的零压流模型(输运方程).该模型是研究狄拉克激波(<span class="formulaText"><inline-formula><tex-math id="M5">$ \delta $</tex-math></inline-formula></span> -激波)和真空形成的最重要模型.自1994年起,它便被人们广泛研究,见文献[<xref ref-type="bibr" rid="b1">1</xref>, <xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b20">20</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]等.特别地, Bouchut首次给出了其黎曼问题测度解的存在性<sup>[<xref ref-type="bibr" rid="b1">1</xref>]</sup>,丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... [<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 证明了其初值为可测函数时柯西问题弱解的存在性和唯一性.紧接着,在文献[<xref ref-type="bibr" rid="b10">10</xref>]中,黄飞敏和王振又将结果推广到初值为Radon测度的情形.此后,对于含各种形式非齐次项的零压流方程陆续有了相关研究结果<sup>[<xref ref-type="bibr" rid="b2">2</xref>, <xref ref-type="bibr" rid="b5">5</xref>, <xref ref-type="bibr" rid="b17">17</xref>]</sup>.在这些文献的基础上,本文给出了初值问题(1.1)–(1.2)弱解的存在性,唯一性和大时间渐近行为等方面新的结果.在后面的研究中,作者还将在本文研究基础上进一步考虑含间断非齐次项的零压流的初值问题. ...</div> </div> </div> <div id="article_reference_meta_b11"> <div id="article_reference_meta_b11_title" class="title_">Well posedness for pressureless Euler system with a flocking dissipation in Wasserstein space</div> <div id="article_reference_meta_b11_citedNumber">3</div> <div id="article_reference_meta_b11_nian">2015</div> <div id="article_reference_meta_b11_jcr"></div> <div id="article_reference_meta_b11_cjcr"></div> <div id="article_reference_meta_b11_articleCitedText"> <div class="sentence">... 模型(1.1)是群体运动模型Cucker-Smale模型趋于平衡态时的动力学描述,其详细推导可参考文献[<xref ref-type="bibr" rid="b8">8</xref>].目前已经得到关于该模型的一些适定性结果<sup>[<xref ref-type="bibr" rid="b8">8</xref>, <xref ref-type="bibr" rid="b11">11</xref>-<xref ref-type="bibr" rid="b12">12</xref>]</sup>. Cucker-Smale模型是描述群体现象的一个离散模型,其动力学方面的研究近年来受到了广泛关注,比如文献[<xref ref-type="bibr" rid="b9">9</xref>]中关于渐近行为和稳定性的研究. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 对于模型(1.1), Ha,黄飞敏和王益等在2014年首次推导出了该模型,并通过引入广义势得到了当初值<span class="formulaText"><inline-formula><tex-math id="M8">$ \rho_{0}\in L_{loc}^{1}({\Bbb R}) $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M9">$ u_{0}\in L^{\infty}({\Bbb R}) $</tex-math></inline-formula></span>时其整体熵解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b8">8</xref>]</sup>.随后,金春银将他们的结果推广到<span class="formulaText"><inline-formula><tex-math id="M11">$ \rho_{0} $</tex-math></inline-formula></span>是Radon测度, <span class="formulaText"><inline-formula><tex-math id="M12">$ u_{0}\in L^{\infty}(\rho_{0}) $</tex-math></inline-formula></span>的情形<sup>[<xref ref-type="bibr" rid="b12">12</xref>]</sup>,并得到了该模型在Wasserstein空间的适定性<sup>[<xref ref-type="bibr" rid="b11">11</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 对于模型(1.1)的黎曼问题,我们知道<span class="formulaText"><inline-formula><tex-math id="M15">$ \delta $</tex-math></inline-formula></span> -激波和真空确实会出现<sup>[<xref ref-type="bibr" rid="b8">8</xref>, <xref ref-type="bibr" rid="b11">11</xref>]</sup>.另外,基本波的相互作用在理论、数值计算和应用方面都起着很重要的作用.因此,本文中我们主要研究模型(1.1)初值含<span class="formulaText"><inline-formula><tex-math id="M17">$ \delta $</tex-math></inline-formula></span> -测度的扰动黎曼问题和包含<span class="formulaText"><inline-formula><tex-math id="M18">$ \delta $</tex-math></inline-formula></span> -激波和真空的所有可能的波的相互作用,即我们重点关注模型(1.1)的如下初值问题 ...</div> </div> </div> <div id="article_reference_meta_b12"> <div id="article_reference_meta_b12_title" class="title_">Existence and uniqueness of entropy solution to pressureless Euler system with a flocking dissipation</div> <div id="article_reference_meta_b12_citedNumber">2</div> <div id="article_reference_meta_b12_nian">2016</div> <div id="article_reference_meta_b12_jcr"></div> <div id="article_reference_meta_b12_cjcr"></div> <div id="article_reference_meta_b12_articleCitedText"> <div class="sentence">... 模型(1.1)是群体运动模型Cucker-Smale模型趋于平衡态时的动力学描述,其详细推导可参考文献[<xref ref-type="bibr" rid="b8">8</xref>].目前已经得到关于该模型的一些适定性结果<sup>[<xref ref-type="bibr" rid="b8">8</xref>, <xref ref-type="bibr" rid="b11">11</xref>-<xref ref-type="bibr" rid="b12">12</xref>]</sup>. Cucker-Smale模型是描述群体现象的一个离散模型,其动力学方面的研究近年来受到了广泛关注,比如文献[<xref ref-type="bibr" rid="b9">9</xref>]中关于渐近行为和稳定性的研究. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 对于模型(1.1), Ha,黄飞敏和王益等在2014年首次推导出了该模型,并通过引入广义势得到了当初值<span class="formulaText"><inline-formula><tex-math id="M8">$ \rho_{0}\in L_{loc}^{1}({\Bbb R}) $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M9">$ u_{0}\in L^{\infty}({\Bbb R}) $</tex-math></inline-formula></span>时其整体熵解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b8">8</xref>]</sup>.随后,金春银将他们的结果推广到<span class="formulaText"><inline-formula><tex-math id="M11">$ \rho_{0} $</tex-math></inline-formula></span>是Radon测度, <span class="formulaText"><inline-formula><tex-math id="M12">$ u_{0}\in L^{\infty}(\rho_{0}) $</tex-math></inline-formula></span>的情形<sup>[<xref ref-type="bibr" rid="b12">12</xref>]</sup>,并得到了该模型在Wasserstein空间的适定性<sup>[<xref ref-type="bibr" rid="b11">11</xref>]</sup>. ...</div> </div> </div> <div id="article_reference_meta_b13"> <div id="article_reference_meta_b13_title" class="title_">Singular solutions of a fully nonlinear 2×2 system of conservation laws</div> <div id="article_reference_meta_b13_citedNumber">1</div> <div id="article_reference_meta_b13_nian">2012</div> <div id="article_reference_meta_b13_jcr"></div> <div id="article_reference_meta_b13_cjcr"></div> <div id="article_reference_meta_b13_articleCitedText"> <div class="sentence">... 为方便起见,我们选择参数<span class="formulaText"><inline-formula><tex-math id="M60">$ s = t $</tex-math></inline-formula></span>,并用<span class="formulaText"><inline-formula><tex-math id="M61">$ w(t) = \sqrt{1+{x'(t)}^2}p(t) $</tex-math></inline-formula></span>来表示<span class="formulaText"><inline-formula><tex-math id="M62">$ \delta $</tex-math></inline-formula></span> -激波的强度(质量).接下来,我们将给出黎曼问题(1.1), (2.1)的<span class="formulaText"><inline-formula><tex-math id="M63">$ \delta $</tex-math></inline-formula></span> -激波解的定义.该定义框架由Danilov和Shelkovich<sup>[<xref ref-type="bibr" rid="b3">3</xref>-<xref ref-type="bibr" rid="b4">4</xref>]</sup>提出,并经Kalisch和Mitrovic<sup>[<xref ref-type="bibr" rid="b13">13</xref>-<xref ref-type="bibr" rid="b14">14</xref>]</sup>发展而来. ...</div> </div> </div> <div id="article_reference_meta_b14"> <div id="article_reference_meta_b14_title" class="title_">Singular solutions for shallow water equations</div> <div id="article_reference_meta_b14_citedNumber">1</div> <div id="article_reference_meta_b14_nian">2012</div> <div id="article_reference_meta_b14_jcr"></div> <div id="article_reference_meta_b14_cjcr"></div> <div id="article_reference_meta_b14_articleCitedText"> <div class="sentence">... 为方便起见,我们选择参数<span class="formulaText"><inline-formula><tex-math id="M60">$ s = t $</tex-math></inline-formula></span>,并用<span class="formulaText"><inline-formula><tex-math id="M61">$ w(t) = \sqrt{1+{x'(t)}^2}p(t) $</tex-math></inline-formula></span>来表示<span class="formulaText"><inline-formula><tex-math id="M62">$ \delta $</tex-math></inline-formula></span> -激波的强度(质量).接下来,我们将给出黎曼问题(1.1), (2.1)的<span class="formulaText"><inline-formula><tex-math id="M63">$ \delta $</tex-math></inline-formula></span> -激波解的定义.该定义框架由Danilov和Shelkovich<sup>[<xref ref-type="bibr" rid="b3">3</xref>-<xref ref-type="bibr" rid="b4">4</xref>]</sup>提出,并经Kalisch和Mitrovic<sup>[<xref ref-type="bibr" rid="b13">13</xref>-<xref ref-type="bibr" rid="b14">14</xref>]</sup>发展而来. ...</div> </div> </div> <div id="article_reference_meta_b15"> <div id="article_reference_meta_b15_title" class="title_"></div> <div id="article_reference_meta_b15_citedNumber">2</div> <div id="article_reference_meta_b15_nian"></div> <div id="article_reference_meta_b15_jcr"></div> <div id="article_reference_meta_b15_cjcr"></div> <div id="article_reference_meta_b15_articleCitedText"> <div class="sentence">... 当(1.1)式右端的非齐次项为零时,它就是人们常见的零压流模型(输运方程).该模型是研究狄拉克激波(<span class="formulaText"><inline-formula><tex-math id="M5">$ \delta $</tex-math></inline-formula></span> -激波)和真空形成的最重要模型.自1994年起,它便被人们广泛研究,见文献[<xref ref-type="bibr" rid="b1">1</xref>, <xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b20">20</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]等.特别地, Bouchut首次给出了其黎曼问题测度解的存在性<sup>[<xref ref-type="bibr" rid="b1">1</xref>]</sup>,丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M19">$ \delta $</tex-math></inline-formula></span>是标准的狄拉克函数, <span class="formulaText"><inline-formula><tex-math id="M20">$ m_0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M21">$ u_0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M22">$ \rho_\pm $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M23">$ u_\pm $</tex-math></inline-formula></span>是任意常数.因为模型(1.1)的黎曼解中出现了<span class="formulaText"><inline-formula><tex-math id="M24">$ \delta $</tex-math></inline-formula></span> -激波,很自然地我们要考虑其初值含<span class="formulaText"><inline-formula><tex-math id="M25">$ \delta $</tex-math></inline-formula></span> -测度的初值问题(1.2).对于零压流、Chaplygin气体方程和其他方程类似初值问题的研究,可参考文献[<xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b25">25</xref>-<xref ref-type="bibr" rid="b27">27</xref>]. ...</div> </div> </div> <div id="article_reference_meta_b16"> <div id="article_reference_meta_b16_title" class="title_">Interactions of delta shock waves in a strictly hyperbolic system of conservation laws</div> <div id="article_reference_meta_b16_citedNumber">2</div> <div id="article_reference_meta_b16_nian">2008</div> <div id="article_reference_meta_b16_jcr"></div> <div id="article_reference_meta_b16_cjcr"></div> <div id="article_reference_meta_b16_articleCitedText"> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M26">$ \epsilon $</tex-math></inline-formula></span>是充分小的正数.我们构造出了问题(1.1), (1.3)的整体解,并得到了其大时间渐近行为.而且,在构造解的过程中,我们还发现了一种新的非经典解:<span class="formulaText"><inline-formula><tex-math id="M27">$ \delta $</tex-math></inline-formula></span> -接触间断解. <span class="formulaText"><inline-formula><tex-math id="M28">$ \delta $</tex-math></inline-formula></span> -接触间断是一种包含<span class="formulaText"><inline-formula><tex-math id="M29">$ \delta $</tex-math></inline-formula></span> -函数形式的解,其支集在接触间断上.该形式的非经典解曾出现在磁流体力学方程和零压流的基本波的相互作用过程中<sup>[<xref ref-type="bibr" rid="b16">16</xref>, <xref ref-type="bibr" rid="b19">19</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 其中, <span class="formulaText"><inline-formula><tex-math id="M116">$ \delta J $</tex-math></inline-formula></span>的传播速度为<span class="formulaText"><inline-formula><tex-math id="M117">$ u_0e^{-t} $</tex-math></inline-formula></span>, "<span class="formulaText"><inline-formula><tex-math id="M118">$ (\pm) $</tex-math></inline-formula></span>"代表"<span class="formulaText"><inline-formula><tex-math id="M119">$ (\rho_{\pm}, u_{\pm}e^{-t}) $</tex-math></inline-formula></span>", "<span class="formulaText"><inline-formula><tex-math id="M120">$ (0) $</tex-math></inline-formula></span>"代表"<span class="formulaText"><inline-formula><tex-math id="M121">$ (\frac{m_{0}}{2\epsilon}, u_{0}e^{-t}) $</tex-math></inline-formula></span>".这里的<span class="formulaText"><inline-formula><tex-math id="M122">$ \delta J $</tex-math></inline-formula></span>是一种新的非经典波:<span class="formulaText"><inline-formula><tex-math id="M123">$ \delta $</tex-math></inline-formula></span> -接触间断,即<span class="formulaText"><inline-formula><tex-math id="M124">$ \delta $</tex-math></inline-formula></span> -函数支集在接触间断上,此类波在文献[<xref ref-type="bibr" rid="b16">16</xref>, <xref ref-type="bibr" rid="b19">19</xref>]中也有出现.很容易验证<span class="formulaText"><inline-formula><tex-math id="M125">$ \delta J $</tex-math></inline-formula></span>满足广义Rankine-Hugoniot条件(2.11)和初值条件<span class="formulaText"><inline-formula><tex-math id="M126">$ (x, w, u_\delta)(0) = (0, m_0, u_0), $</tex-math></inline-formula></span>其中<span class="formulaText"><inline-formula><tex-math id="M127">$ \rho_- = \rho_+ = 0 $</tex-math></inline-formula></span><span class="formulaNumber">.</span> ...</div> </div> </div> <div id="article_reference_meta_b17"> <div id="article_reference_meta_b17_title" class="title_">The Riemann problem for the pressureless Euler system with the Coulomb-like friction term</div> <div id="article_reference_meta_b17_citedNumber">3</div> <div id="article_reference_meta_b17_nian">2016</div> <div id="article_reference_meta_b17_jcr"></div> <div id="article_reference_meta_b17_cjcr"></div> <div id="article_reference_meta_b17_articleCitedText"> <div class="sentence">... 证明了其初值为可测函数时柯西问题弱解的存在性和唯一性.紧接着,在文献[<xref ref-type="bibr" rid="b10">10</xref>]中,黄飞敏和王振又将结果推广到初值为Radon测度的情形.此后,对于含各种形式非齐次项的零压流方程陆续有了相关研究结果<sup>[<xref ref-type="bibr" rid="b2">2</xref>, <xref ref-type="bibr" rid="b5">5</xref>, <xref ref-type="bibr" rid="b17">17</xref>]</sup>.在这些文献的基础上,本文给出了初值问题(1.1)–(1.2)弱解的存在性,唯一性和大时间渐近行为等方面新的结果.在后面的研究中,作者还将在本文研究基础上进一步考虑含间断非齐次项的零压流的初值问题. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 情形三   <span class="formulaText"><inline-formula><tex-math id="M53">$ u_{-}>u_{+} $</tex-math></inline-formula></span><span class="formulaNumber">.</span>这种情形中,很容易看到从左状态发出的特征线和从右状态发出的特征线将会相交,从而形成非经典解:<span class="formulaText"><inline-formula><tex-math id="M54">$ \delta $</tex-math></inline-formula></span> -激波.为了在非经典解的框架下求解黎曼问题(1.1), (2.1),类似于文献[<xref ref-type="bibr" rid="b17">17</xref>],我们将引入支集在一条曲线上的加权<span class="formulaText"><inline-formula><tex-math id="M55">$ \delta $</tex-math></inline-formula></span> -测度解. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 这里<span class="formulaText"><inline-formula><tex-math id="M82">$ [\rho] = \rho_+-\rho_- $</tex-math></inline-formula></span><span class="formulaNumber">.</span>广义Rankine-Hugoniot条件的推导可参考文献[<xref ref-type="bibr" rid="b17">17</xref>-<xref ref-type="bibr" rid="b18">18</xref>, <xref ref-type="bibr" rid="b21">21</xref>],此处从略.另外,为保证黎曼解的唯一性, <span class="formulaText"><inline-formula><tex-math id="M83">$ \delta $</tex-math></inline-formula></span> -激波还应满足如下的广义熵条件 ...</div> </div> </div> <div id="article_reference_meta_b18"> <div id="article_reference_meta_b18_title" class="title_">The Riemann problem for the Chaplygin gas equations with a source term</div> <div id="article_reference_meta_b18_citedNumber">1</div> <div id="article_reference_meta_b18_nian">1999</div> <div id="article_reference_meta_b18_jcr"></div> <div id="article_reference_meta_b18_cjcr"></div> <div id="article_reference_meta_b18_articleCitedText"> <div class="sentence">... 这里<span class="formulaText"><inline-formula><tex-math id="M82">$ [\rho] = \rho_+-\rho_- $</tex-math></inline-formula></span><span class="formulaNumber">.</span>广义Rankine-Hugoniot条件的推导可参考文献[<xref ref-type="bibr" rid="b17">17</xref>-<xref ref-type="bibr" rid="b18">18</xref>, <xref ref-type="bibr" rid="b21">21</xref>],此处从略.另外,为保证黎曼解的唯一性, <span class="formulaText"><inline-formula><tex-math id="M83">$ \delta $</tex-math></inline-formula></span> -激波还应满足如下的广义熵条件 ...</div> </div> </div> <div id="article_reference_meta_b19"> <div id="article_reference_meta_b19_title" class="title_">Interactions of delta shocks for transport equations with split delta functions</div> <div id="article_reference_meta_b19_citedNumber">3</div> <div id="article_reference_meta_b19_nian">2009</div> <div id="article_reference_meta_b19_jcr"></div> <div id="article_reference_meta_b19_cjcr"></div> <div id="article_reference_meta_b19_articleCitedText"> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M26">$ \epsilon $</tex-math></inline-formula></span>是充分小的正数.我们构造出了问题(1.1), (1.3)的整体解,并得到了其大时间渐近行为.而且,在构造解的过程中,我们还发现了一种新的非经典解:<span class="formulaText"><inline-formula><tex-math id="M27">$ \delta $</tex-math></inline-formula></span> -接触间断解. <span class="formulaText"><inline-formula><tex-math id="M28">$ \delta $</tex-math></inline-formula></span> -接触间断是一种包含<span class="formulaText"><inline-formula><tex-math id="M29">$ \delta $</tex-math></inline-formula></span> -函数形式的解,其支集在接触间断上.该形式的非经典解曾出现在磁流体力学方程和零压流的基本波的相互作用过程中<sup>[<xref ref-type="bibr" rid="b16">16</xref>, <xref ref-type="bibr" rid="b19">19</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M52">$ u_{-}<u_*<u_{+} $</tex-math></inline-formula></span><span class="formulaNumber">.</span>此处类似于文献[<xref ref-type="bibr" rid="b19">19</xref>],我们将真空视为特殊的稀疏波解,从而对它赋予了伪速度:特征线速度.本文中对真空我们都将这样处理,后面不再赘述. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 其中, <span class="formulaText"><inline-formula><tex-math id="M116">$ \delta J $</tex-math></inline-formula></span>的传播速度为<span class="formulaText"><inline-formula><tex-math id="M117">$ u_0e^{-t} $</tex-math></inline-formula></span>, "<span class="formulaText"><inline-formula><tex-math id="M118">$ (\pm) $</tex-math></inline-formula></span>"代表"<span class="formulaText"><inline-formula><tex-math id="M119">$ (\rho_{\pm}, u_{\pm}e^{-t}) $</tex-math></inline-formula></span>", "<span class="formulaText"><inline-formula><tex-math id="M120">$ (0) $</tex-math></inline-formula></span>"代表"<span class="formulaText"><inline-formula><tex-math id="M121">$ (\frac{m_{0}}{2\epsilon}, u_{0}e^{-t}) $</tex-math></inline-formula></span>".这里的<span class="formulaText"><inline-formula><tex-math id="M122">$ \delta J $</tex-math></inline-formula></span>是一种新的非经典波:<span class="formulaText"><inline-formula><tex-math id="M123">$ \delta $</tex-math></inline-formula></span> -接触间断,即<span class="formulaText"><inline-formula><tex-math id="M124">$ \delta $</tex-math></inline-formula></span> -函数支集在接触间断上,此类波在文献[<xref ref-type="bibr" rid="b16">16</xref>, <xref ref-type="bibr" rid="b19">19</xref>]中也有出现.很容易验证<span class="formulaText"><inline-formula><tex-math id="M125">$ \delta J $</tex-math></inline-formula></span>满足广义Rankine-Hugoniot条件(2.11)和初值条件<span class="formulaText"><inline-formula><tex-math id="M126">$ (x, w, u_\delta)(0) = (0, m_0, u_0), $</tex-math></inline-formula></span>其中<span class="formulaText"><inline-formula><tex-math id="M127">$ \rho_- = \rho_+ = 0 $</tex-math></inline-formula></span><span class="formulaNumber">.</span> ...</div> </div> </div> <div id="article_reference_meta_b20"> <div id="article_reference_meta_b20_title" class="title_"></div> <div id="article_reference_meta_b20_citedNumber">1</div> <div id="article_reference_meta_b20_nian"></div> <div id="article_reference_meta_b20_jcr"></div> <div id="article_reference_meta_b20_cjcr"></div> <div id="article_reference_meta_b20_articleCitedText"> <div class="sentence">... 当(1.1)式右端的非齐次项为零时,它就是人们常见的零压流模型(输运方程).该模型是研究狄拉克激波(<span class="formulaText"><inline-formula><tex-math id="M5">$ \delta $</tex-math></inline-formula></span> -激波)和真空形成的最重要模型.自1994年起,它便被人们广泛研究,见文献[<xref ref-type="bibr" rid="b1">1</xref>, <xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b20">20</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]等.特别地, Bouchut首次给出了其黎曼问题测度解的存在性<sup>[<xref ref-type="bibr" rid="b1">1</xref>]</sup>,丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> </div> </div> <div id="article_reference_meta_b21"> <div id="article_reference_meta_b21_title" class="title_">The exact Riemann solutions to the generalized Chaplygin gas equations with friction</div> <div id="article_reference_meta_b21_citedNumber">1</div> <div id="article_reference_meta_b21_nian">2016</div> <div id="article_reference_meta_b21_jcr"></div> <div id="article_reference_meta_b21_cjcr"></div> <div id="article_reference_meta_b21_articleCitedText"> <div class="sentence">... 这里<span class="formulaText"><inline-formula><tex-math id="M82">$ [\rho] = \rho_+-\rho_- $</tex-math></inline-formula></span><span class="formulaNumber">.</span>广义Rankine-Hugoniot条件的推导可参考文献[<xref ref-type="bibr" rid="b17">17</xref>-<xref ref-type="bibr" rid="b18">18</xref>, <xref ref-type="bibr" rid="b21">21</xref>],此处从略.另外,为保证黎曼解的唯一性, <span class="formulaText"><inline-formula><tex-math id="M83">$ \delta $</tex-math></inline-formula></span> -激波还应满足如下的广义熵条件 ...</div> </div> </div> <div id="article_reference_meta_b22"> <div id="article_reference_meta_b22_title" class="title_">The Riemann problem with delta data for zero-pressure gas dynamcis</div> <div id="article_reference_meta_b22_citedNumber">1</div> <div id="article_reference_meta_b22_nian">2016</div> <div id="article_reference_meta_b22_jcr"></div> <div id="article_reference_meta_b22_cjcr"></div> <div id="article_reference_meta_b22_articleCitedText"> <div class="sentence">... 接下来,令<span class="formulaText"><inline-formula><tex-math id="M31">$ \epsilon\rightarrow0 $</tex-math></inline-formula></span>,由弱解的稳定性理论,并结合广义Rankine-Hugoniot条件和广义熵条件,我们构造性地得到了模型(1.1)–(1.2)的唯一整体解.而且,其解中也包含了<span class="formulaText"><inline-formula><tex-math id="M32">$ \delta $</tex-math></inline-formula></span> -接触间断.进一步地,取<span class="formulaText"><inline-formula><tex-math id="M33">$ m_{0} = 0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M34">$ u_{0} = 0 $</tex-math></inline-formula></span>,模型(1.1)–(1.2)的解正好对应于(1.1)的黎曼解.在文献[<xref ref-type="bibr" rid="b25">25</xref>]中,作者和其导师首次应用本文中构造解的方法成功解决了一维Chaplygin气体初值含<span class="formulaText"><inline-formula><tex-math id="M35">$ \delta $</tex-math></inline-formula></span> -函数的初值问题.近年来,该方法已经被应用于研究很多相关方程组的类似问题<sup>[<xref ref-type="bibr" rid="b7">7</xref>, <xref ref-type="bibr" rid="b22">22</xref>]</sup>. ...</div> </div> </div> <div id="article_reference_meta_b23"> <div id="article_reference_meta_b23_title" class="title_">Uniqueness of generalized solution for the Cauchy problem of transportation equations</div> <div id="article_reference_meta_b23_citedNumber">3</div> <div id="article_reference_meta_b23_nian">1997</div> <div id="article_reference_meta_b23_jcr"></div> <div id="article_reference_meta_b23_cjcr"></div> <div id="article_reference_meta_b23_articleCitedText"> <div class="sentence">... 当(1.1)式右端的非齐次项为零时,它就是人们常见的零压流模型(输运方程).该模型是研究狄拉克激波(<span class="formulaText"><inline-formula><tex-math id="M5">$ \delta $</tex-math></inline-formula></span> -激波)和真空形成的最重要模型.自1994年起,它便被人们广泛研究,见文献[<xref ref-type="bibr" rid="b1">1</xref>, <xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b20">20</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]等.特别地, Bouchut首次给出了其黎曼问题测度解的存在性<sup>[<xref ref-type="bibr" rid="b1">1</xref>]</sup>,丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... , <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 在文献[<xref ref-type="bibr" rid="b23">23</xref>]和[<xref ref-type="bibr" rid="b24">24</xref>]中,丁夏畦,黄飞敏和王振研究了齐次的零压流方程 ...</div> </div> </div> <div id="article_reference_meta_b24"> <div id="article_reference_meta_b24_title" class="title_">On the Cauchy problem of transportation equations</div> <div id="article_reference_meta_b24_citedNumber">3</div> <div id="article_reference_meta_b24_nian">1997</div> <div id="article_reference_meta_b24_jcr"></div> <div id="article_reference_meta_b24_cjcr"></div> <div id="article_reference_meta_b24_articleCitedText"> <div class="sentence">... 当(1.1)式右端的非齐次项为零时,它就是人们常见的零压流模型(输运方程).该模型是研究狄拉克激波(<span class="formulaText"><inline-formula><tex-math id="M5">$ \delta $</tex-math></inline-formula></span> -激波)和真空形成的最重要模型.自1994年起,它便被人们广泛研究,见文献[<xref ref-type="bibr" rid="b1">1</xref>, <xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b20">20</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]等.特别地, Bouchut首次给出了其黎曼问题测度解的存在性<sup>[<xref ref-type="bibr" rid="b1">1</xref>]</sup>,丁夏畦、黄飞敏和王振等通过引入广义势给出了初值包含Radon测度时其柯西问题整体解的存在性和唯一性<sup>[<xref ref-type="bibr" rid="b10">10</xref>, <xref ref-type="bibr" rid="b23">23</xref>-<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... -<xref ref-type="bibr" rid="b24">24</xref>]</sup>. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 在文献[<xref ref-type="bibr" rid="b23">23</xref>]和[<xref ref-type="bibr" rid="b24">24</xref>]中,丁夏畦,黄飞敏和王振研究了齐次的零压流方程 ...</div> </div> </div> <div id="article_reference_meta_b25"> <div id="article_reference_meta_b25_title" class="title_">The Riemann problem with delta initial data for the one-dimensional Chaplygin gas equations</div> <div id="article_reference_meta_b25_citedNumber">2</div> <div id="article_reference_meta_b25_nian">2012</div> <div id="article_reference_meta_b25_jcr"></div> <div id="article_reference_meta_b25_cjcr"></div> <div id="article_reference_meta_b25_articleCitedText"> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M19">$ \delta $</tex-math></inline-formula></span>是标准的狄拉克函数, <span class="formulaText"><inline-formula><tex-math id="M20">$ m_0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M21">$ u_0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M22">$ \rho_\pm $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M23">$ u_\pm $</tex-math></inline-formula></span>是任意常数.因为模型(1.1)的黎曼解中出现了<span class="formulaText"><inline-formula><tex-math id="M24">$ \delta $</tex-math></inline-formula></span> -激波,很自然地我们要考虑其初值含<span class="formulaText"><inline-formula><tex-math id="M25">$ \delta $</tex-math></inline-formula></span> -测度的初值问题(1.2).对于零压流、Chaplygin气体方程和其他方程类似初值问题的研究,可参考文献[<xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b25">25</xref>-<xref ref-type="bibr" rid="b27">27</xref>]. ...</div> <div class="boundary"><p class="ty-x"></p></div> <div class="sentence">... 接下来,令<span class="formulaText"><inline-formula><tex-math id="M31">$ \epsilon\rightarrow0 $</tex-math></inline-formula></span>,由弱解的稳定性理论,并结合广义Rankine-Hugoniot条件和广义熵条件,我们构造性地得到了模型(1.1)–(1.2)的唯一整体解.而且,其解中也包含了<span class="formulaText"><inline-formula><tex-math id="M32">$ \delta $</tex-math></inline-formula></span> -接触间断.进一步地,取<span class="formulaText"><inline-formula><tex-math id="M33">$ m_{0} = 0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M34">$ u_{0} = 0 $</tex-math></inline-formula></span>,模型(1.1)–(1.2)的解正好对应于(1.1)的黎曼解.在文献[<xref ref-type="bibr" rid="b25">25</xref>]中,作者和其导师首次应用本文中构造解的方法成功解决了一维Chaplygin气体初值含<span class="formulaText"><inline-formula><tex-math id="M35">$ \delta $</tex-math></inline-formula></span> -函数的初值问题.近年来,该方法已经被应用于研究很多相关方程组的类似问题<sup>[<xref ref-type="bibr" rid="b7">7</xref>, <xref ref-type="bibr" rid="b22">22</xref>]</sup>. ...</div> </div> </div> <div id="article_reference_meta_b26"> <div id="article_reference_meta_b26_title" class="title_">Generalized plane delta-shock waves for n-dimensional zero-pressure gas dynamics</div> <div id="article_reference_meta_b26_citedNumber">0</div> <div id="article_reference_meta_b26_nian">2001</div> <div id="article_reference_meta_b26_jcr"></div> <div id="article_reference_meta_b26_cjcr"></div> </div> <div id="article_reference_meta_b27"> <div id="article_reference_meta_b27_title" class="title_">The Riemann problem with delta initial data for a class of coupled hyperbolic system of conservation laws</div> <div id="article_reference_meta_b27_citedNumber">1</div> <div id="article_reference_meta_b27_nian">2007</div> <div id="article_reference_meta_b27_jcr"></div> <div id="article_reference_meta_b27_cjcr"></div> <div id="article_reference_meta_b27_articleCitedText"> <div class="sentence">... 其中<span class="formulaText"><inline-formula><tex-math id="M19">$ \delta $</tex-math></inline-formula></span>是标准的狄拉克函数, <span class="formulaText"><inline-formula><tex-math id="M20">$ m_0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M21">$ u_0 $</tex-math></inline-formula></span>, <span class="formulaText"><inline-formula><tex-math id="M22">$ \rho_\pm $</tex-math></inline-formula></span>和<span class="formulaText"><inline-formula><tex-math id="M23">$ u_\pm $</tex-math></inline-formula></span>是任意常数.因为模型(1.1)的黎曼解中出现了<span class="formulaText"><inline-formula><tex-math id="M24">$ \delta $</tex-math></inline-formula></span> -激波,很自然地我们要考虑其初值含<span class="formulaText"><inline-formula><tex-math id="M25">$ \delta $</tex-math></inline-formula></span> -测度的初值问题(1.2).对于零压流、Chaplygin气体方程和其他方程类似初值问题的研究,可参考文献[<xref ref-type="bibr" rid="b6">6</xref>, <xref ref-type="bibr" rid="b15">15</xref>, <xref ref-type="bibr" rid="b25">25</xref>-<xref ref-type="bibr" rid="b27">27</xref>]. ...</div> </div> </div> </div> </div> </div> </div> <div class="cankaowenxian1"></div> <div class="col-xs-3"> <div class="slide" style="top: 367px; display: block;"> <div id="sideToolbar"> <div id="sideCatalog" class="sideCatalogBg"> <div id="sideCatalog-sidebar"> <div class="sideCatalog-sidebar-top"></div> <div class="sideCatalog-sidebar-bottom"></div> </div> <div id="sideCatalog-updown"> <div id="sideCatalog-up" class="sideCatalog-up-disable" title="up"></div> <div id="sideCatalog-down" class="sideCatalog-down-enable" title="down"></div> </div> <div id="sideCatalog-catalog"> <dl style="width: 175px; zoom: 1; top: 0px;" id="outline_dl"> </dl> </div> </div> <i id="sideToolbar-up" style="float:left;"></i> <i id="sideCatalogBtn" style="float:left;"></i> </div> </div> </div> </div> </div> </div> </div> <div class="motaikuang" onclick="guanbiann()"></div> <div class="tupiankuang"> <i class="glyphicon glyphicon-remove-circle guanbi" onclick="guanbiann();"></i> <p class="biaotitupiana"> <span class="yige"></span>/<span class="zongdea"></span> </p> <div class="imgaesa"> <table class="haoshi"> <tr> <td onclick="shang();" class="zuo" > 〈 </td> <td class="zhong"> <img src="" class="tp" onload="xianss2()"> </td> <td onclick="xia();" class="you" > 〉 </td> </tr> </table> </div> <div class="neirong"></div> </div> <div class="biaokuang"> <i class="glyphicon glyphicon-remove-circle guanbi" onclick="guanbiann();"></i> <div class="tuti"></div> <div class="table-responsive liuliu"></div> <div class="biaoshuo"> <p class="mtk-biaoshoen"></p> <p class="mtk-biaoshocn"></p> </div> </div> <div class="qipao-zong" onmouseleave="yichu()"> <div class="qipao-content"> </div> <div class="qipao-jiantou"> <img src="../../../richhtml/1003-3998/richHtml_jats1_1/images/1.png"> </div> </div> </div> </div> </div> <!--底部--> <div class="jiewei" align="center"> <!--底部--> <div class="footer"> <div class="banquan"> 版权所有 © 《数学物理学报》杂志社<br> 地址： 武汉市71010号信箱(430071)　电话: 027-87199206(中文版)　027-87199087(英文版) <br> E-mail: actams@apm.ac.cn<br> 本系统由北京玛格泰克科技发展有限公司设计开发 </div> </div> <!--底部end--> <!--返回顶部--> <div class="top_web" id="backtop" style="display:block;"> <span class="glyphicon glyphicon-chevron-up" aria-hidden="true" ></span> </div> <script src="http://121.43.60.238/sxwlxbA/images/1003-3998/js/backtop.js"></script> <!--返回顶部end--> </div> </body> <script type="text/javascript" src="../../../richhtml/1003-3998/richHtml_jats1_1/js/wangkan.js"></script> <script src="../../../richhtml/1003-3998/richHtml_jats1_1/js/qrcode.js"></script> <script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script> <script type="text/x-mathjax-config"> MathJax.Hub.Config({ extensions: ["tex2jax.js"], jax: ["input/TeX", "output/HTML-CSS"], tex2jax: {inlineMath: [ ['$','$'], ["\\(","\\)"] ],displayMath: [ ['$$','$$'], ["\\[","\\]"] ],processEscapes: true}, "HTML-CSS": { availableFonts: ["TeX"] }, TeX: {equationNumbers: {autoNumber: ["none"], useLabelIds: true}}, "HTML-CSS": {linebreaks: {automatic: true}}, SVG: {linebreaks: {automatic: true}} }); $(function() { $(".keyword").each(function() { // key var key = $(this); // value var value = key.text(); // 添加点击事件 $(key).click(function() { // 创建一个form表单 var form = document.createElement("form"); form.method = "post"; form.action = "http://121.43.60.238/sxwlxbA/CN/article/searchArticleResult.do"; form.target = "_blank"; // 将form表单添加到body标签中 document.body.appendChild(form); // 新建表单标签 var formElement = document.createElement("input"); formElement.name = "searchSQL"; formElement.type = "hidden"; formElement.value = "(" + value + "[Keyword])"; form.appendChild(formElement); form.submit(); }); }); }); function sddas(){ $('.kkaqqqq').toggle(); } </script> </html>