1 引言
近些年来,用分数布朗运动来研究金融数学模型已经成为一个重要的发展方向.由于分数布朗运动的“尖峰厚尾性”和“长程记忆性”表现出Gussian分布的特性,所以用Gussian分布能够更好的刻画金融资产模型,相应的随机分析理论见文献[1-3].然而, Tomas[4]]等人的研究表明,在使用分数布朗运动来刻画金融资产价格的波动时仍存在一些不足,基于Wick积分的分数布朗运动在应用于金融计算时受到很大的限制,同时定义一个合适的关于分数布朗运动的随机积分是比较困难的.于是,考虑使用混合分数布朗运动来刻画金融资产的波动是合理的(如Xiao[5], Sun[6], He[7]等). Cheridito[8]最早把布朗运动和分数布朗运动组合在一起研究了欧式期权的定价; Mounir[9]研究了混合分数布朗运动样本轨道的Holder连续性和自相似性;由于分数布朗运动的Itô公式所建立的B-S模型已经远远超越了B-S模型的定义和属性,学者们发现所建立的分数B-S模型不能准确地描述资产的浮动收益和金融市场的波动情形[10].事实上,由于分数布朗运动的自相似性、厚尾性和长程关联性,使得分数布朗运动既不是Markov过程又不是半鞅,这给随机分析和随机计算带来了极大的困难,于是有些学者提出用混合跳扩散分数布朗运动(mjd-fBm)模型来刻画金融市场的波动行为(如Foad[11, 12], Rao[13], Miao[14], Yang[15]等).
关于具有复杂收益结构的奇异型金融衍生证券定价的研究成果并不多见,本文拟通过一个基于标准布朗运动、分数布朗运动、Poisson过程的线性组合的混合跳扩散B-S模型,结合Merton假设条件以及风险资产所满足的随机微分方程的Cauchy初值问题,利用多尺度参数摄动方法(张伟江[16], Nesterov[17], Ma[18], Butuzov[19]等),求解了欧式回望期权所适合的抛物型随机偏微分方程,给出了欧式固定履约价的回望期权的近似定价公式,并利用Feymann-Kac公式分析了近似公式的误差估计.结合已有的成果(Lai[20], Eberlein[21], Leung[22], Park[23], Fuh[24],杨朝强[25, 26]等),文章最后对近似公式作了数值模拟分析.
2 混合跳扩散B-S模型
定义2.1[8] 设Hurst参数为
其中
性质2.1[9] 混合分数布朗运动
(ⅰ)对任意的
(ⅱ)
(ⅲ)对任意的
其中
(ⅳ)对任意的
其中
(ⅴ)当
(ⅵ)
(ⅶ)对任意的
在完备概率空间
引理2.1[15] 设
其中
其中
回望期权是一种典型复杂的新型奇异期权,期权持有者在期权到期日可通过选择资产价格在有效回望期内的最高价格或者最低价格而进行交易.设
设
其中
终端条件为
注意到抛物型随机偏微分方程(2.2)的结构复杂,寻找回望期权的精确解析解是比较困难的[25],其解的结构相当复杂.于是,考虑在混合跳扩散B-S模型下研究回望期权的近似解,不妨设原生资产价格
无风险资产价格
其中
其中
3 多尺度参数摄动方法
定义如下符号
其中
在如上变换下,当
其中
下面对随机偏微分方程初值问题(2.6)采用多尺度参数摄动方法作处理来解决欧式固定履约价的回望期权定价问题.令
把上述级数(3.6)代入到随机偏微分方程初值问题(3.5),可得
其中
由
其中
注意到初值问题(3.5)的初值条件复杂,不妨根据幂级数展式(3.6)对初值问题(3.5)的初值条件进行分解,把抛物型混合跳扩散随机偏微分方程(3.5)的求解问题化归为一组可求解的常系数抛物型混合跳扩散随机偏微分方程的初值问题,其中
下面依次计算
4 定价公式的推导
引理4.1 若
其中
证明详见文献[25].
引理4.2 线性抛物型混合跳扩散随机偏微分方程(3.8)的解可表示为
其中
这里
证 由回望期权的定义,在有效回望期内的任意时刻的价格
则抛物型混合跳扩散随机偏微分方程初值问题(3.8)可以转换为如下形式
对变换(4.1)进行逆变换可完成引理的证明.
由引理4.1,引理4.2以及公式(3.5)和(3.6),易得如下结论成立.
定理4.1 设
其中
这里
同理可证明欧式固定履约回望看涨期权的定价公式,以如下定理给出.
定理4.2 设
其中
这里
5 误差估计
本节内容讨论近似结论(4.4), (4.5)的误差估计问题.先作如下假设
(ⅰ)假设
(ⅱ)假设
(ⅲ)假设对任意的
很显然如上假设中
为了方便证明,令
引理5.1 对任意的
证 由引理4.1容易得到
以及
将公式(5.4)和(5.5)代入
于是
令
根据引理4.2,抛物型混合跳扩散随机偏微分方程初值问题(3.7)的解
由文献[16],存在正常数
将公式(5.7)代入公式(5.6)可得
于是式(5.2)中第二个不等式成立.
引理5.2 对任意的
证明类似引理5.1,结合基本假设(ⅱ)的公式(5.1)可得.
注意到公式(3.2)是初值问题(3.7)的抛物算子,于是可以考虑利用抛物方程的Feyman-Kac公式来研究
由以上的辅助引理,给出本节的两个主要结论.
定理5.1 对于充分小的
证 令
因此,
其中
即
由引理5.1,引理5.2以及公式(5.1),对任意的
把公式(5.2)和公式(5.12)代入公式(5.11),对任意的
不妨对抛物初值问题(5.11)的解
其中
的解,由于随机微分方程(5.15)存在解
显然瑕积分
定理5.2 对于充分小的
证 仿照定理5.1的证明,考察
其中
注意到
所以有
于是
为了估计
进一步将引理5.1的公式(5.2)以及引理5.2的结果代入到公式(5.19),对任意的
由Feynman-Kac公式可知,抛物型混合随机初值问题(5.18)的解可表示为如下形式的条件概率问题
其中
证毕.
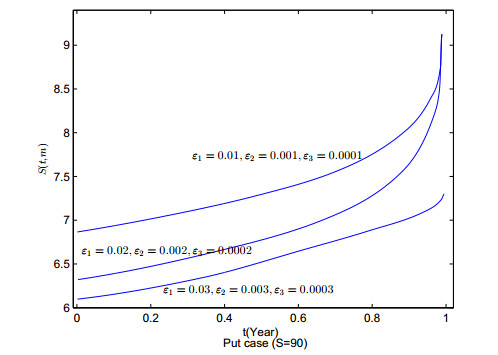
6 数值模拟
本节内容对上节给出的误差估计结果进行数值模拟分析.根据混合分数跳扩散Black-Scholes公式,当波动率
上述模拟中
表 1
欧式固定履约价的回望看跌期权价格
| 股价 | 精确值 | ||||||
| 10 | 71.419978523 | 73.636156468 | 76.519896751 | 81.145748979 | 84.912047501 | 88.658351421 | 87.5310 |
| 20 | 63.260586024 | 65.223576189 | 67.777862873 | 71.875233511 | 75.211250358 | 78.529556890 | 77.5310 |
| 30 | 55.101193512 | 56.810995913 | 59.035828989 | 62.604718032 | 65.510453213 | 68.400762361 | 67.5310 |
| 40 | 46.941801092 | 48.398415621 | 50.293795111 | 53.334202565 | 55.809656065 | 58.271967823 | 57.5310 |
| 50 | 38.782408511 | 39.985835343 | 41.551761231 | 44.063687088 | 46.108858922 | 48.143173289 | 47.5310 |
| 60 | 30.623016001 | 31.573255065 | 32.809727353 | 34.793171621 | 36.408061771 | 38.014378764 | 37.5310 |
| 70 | 22.464439443 | 23.161516031 | 24.068567676 | 25.523583232 | 26.708234734 | 27.886597117 | 27.5320 |
| 80 | 14.368445442 | 14.814301500 | 15.394459401 | 16.325099631 | 17.082812751 | 17.836503307 | 17.6097 |
| 90 | 7.057221764 | 7.276208938 | 7.561159943 | 8.018254242 | 8.390413468 | 8.760596967 | 8.6492 |
表 2
欧式固定履约价的回望看跌期权价格
| 股价 | 精确值 | ||||||
| 10 | 67.386870055 | 71.018366151 | 76.238252122 | 83.309467972 | 86.150639011 | 89.728816161 | 87.5310 |
| 20 | 59.688240989 | 62.904855955 | 67.528394784 | 73.791757867 | 76.308338686 | 79.477726082 | 77.5310 |
| 30 | 51.989611921 | 54.791345753 | 58.818537464 | 64.274047874 | 66.466038363 | 69.226636056 | 67.5310 |
| 40 | 44.290982862 | 46.677835544 | 50.108680141 | 54.756337743 | 56.623738038 | 58.975546033 | 57.5310 |
| 50 | 36.592353837 | 38.564325343 | 41.398822822 | 45.238627682 | 46.781437737 | 48.724456004 | 47.5310 |
| 60 | 28.893724747 | 30.450815141 | 32.688965565 | 35.720917626 | 36.939137373 | 38.473365978 | 37.5310 |
| 70 | 21.195865544 | 22.338116291 | 23.979979171 | 26.204159333 | 27.097821272 | 28.223301060 | 27.5320 |
| 80 | 13.557054821 | 14.287648062 | 15.337797447 | 16.760401881 | 17.331995611 | 18.051862002 | 17.6097 |
| 90 | 6.658698249 | 7.017537244 | 7.533329792 | 8.232057784 | 8.512802401 | 8.866372785 | 8.6492 |
图 1
参考文献
A general fractional white noise theory and applications to finance
DOI:10.1111/1467-9965.00018 [本文引用: 1]
Fractional White noise calculus and applications to finance, infinite dimensional analysis
A note on Wick products and the fractional Black-Scholes model
DOI:10.1007/s00780-004-0144-5 [本文引用: 1]
Pricing model for equity warrants in a mixed fractional Brownian environment and its algorithm
DOI:10.1016/j.physa.2012.07.041 [本文引用: 1]
Pricing currency options in the mixed fractional Brownian motion
DOI:10.1016/j.physa.2013.03.055 [本文引用: 1]
The pricing of credit default swaps under a generalized mixed fractional Brownian motion
Mixed fractional Brownian motion
Pricing by hedging and no-arbitrage beyond semimartingales
DOI:10.1007/s00780-008-0074-8 [本文引用: 2]
Pricing currency option in a mixed fractional Brownian motion with jumps environment
Actuarial approach in a mixed fractional Brownian motion with jumps environment for pricing currency option
Option pricing for processes driven by mixed fractional Brownian motion with superimposed jumps
DOI:10.1017/S0269964815000200 [本文引用: 1]
Pricing model for convertible bonds:A mixed fractional Brownian motion with jumps
DOI:10.4208/eajam.221214.240415a [本文引用: 1]
Optimal exercise boundary of American fractional lookback option in a mixed jump-diffusion fractional Brownian motion environment
Asymptotics of the solution to a singularly perturbed system of parabolic equations in the critical case
DOI:10.1134/S0965542510020077 [本文引用: 1]
A uniform asymptotic expansion for stochastic volatility model in pricing multi-asset European options
DOI:10.1002/asmb.880 [本文引用: 1]
Asymptotics of the solution of an initial-boundary value problem for a singularly perturbed parabolic equation in the case of double root of the degenerate equation
Exercise regions and efficient valuation of American lookback options
DOI:10.1111/j.0960-1627.2004.00191.x [本文引用: 1]
Equivalence of floating and fixed strike Asian and lookback options
DOI:10.1016/j.spa.2004.07.003 [本文引用: 1]
An analytic pricing formula for lookback options under stochastic volatility
DOI:10.1016/j.aml.2012.07.008 [本文引用: 1]
An semi-analytic pricing formula for lookback options under a general stochastic volatility model
DOI:10.1016/j.spl.2013.08.002 [本文引用: 1]
Pricing discrete path-dependent options under a double exponential jump-diffusion model
DOI:10.1016/j.jbankfin.2013.03.023 [本文引用: 1]
一类特殊混合跳-扩散模型的欧式回望期权定价
DOI:10.3969/j.issn.1000-5641.2017.04.001 [本文引用: 4]
Pricing European lookback option by a special kind of mixed jump-diffusion model
DOI:10.3969/j.issn.1000-5641.2017.04.001 [本文引用: 4]
混合跳-扩散模型下一类基金公司的金融债券定价与违约概率研究
DOI:10.3969/j.issn.1001-2362.2018.02.007 [本文引用: 1]
Pricing of fund corporate bonds and default probability study under mixed jump-diffusion model
DOI:10.3969/j.issn.1001-2362.2018.02.007 [本文引用: 1]