1 引言
Doelman等在文献[1]中提出如下空间变量为一维且空间区域为无界区域的广义Gierer-Meinhardt(G-M)方程
这里
这里
以及
系统(1.2)退化为如下经典的G-M系统
我们称方程(1.4)为快系统,其中
三维及以上相空间中的同宿轨道的存在性和稳定性问题,是动力系统领域的困难问题之一.几何奇异摄动理论的快慢分解和降维的思想,或提供了处理上述问题的思路之一.因此, Doelman等[1]引入如下与(1.4)等价的慢系统
其中,
在系统(1.4)和(1.5)中令
和退化系统
其中退化系统(1.7)的动力学被限制在由
和
所组成的二维临界流形上.显然,上述的二维临界流形上的所有点,都是层系统的平衡点. Doelman等[1]证明:当G-M方程(1.2)的参数及非线性项满足一定的条件时,系统(1.2)具有同宿于鞍点
这里
与Melnikov积分相关,其中
这里
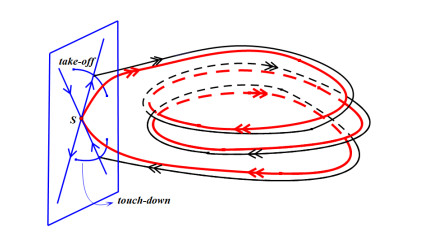
图 1
图 1
奇异3 -脉冲同宿轨道的示意图:双箭头黑色部分代表快的运动段(以经过快场3次为例);单箭头蓝色部分代表两段慢的运动段.图中红色轨道代表从奇异3 -脉冲同宿轨道分支产生的系统(1.2)的3 -脉冲同宿轨道
然而,文献[1]中并没有给出Melnikov积分的计算结果,即没有给出(1.8)式的计算结果和过程.因此,本文的目的有两个:首先,利用初等积分法,给出推导获得二阶非线性保守系统(1.10)的同宿轨道的显式表达式
本文结构安排如下:第2节首先给出获得方程(1.9)同宿轨道显式表达式
2 Melnikov积分及其计算
2.1 一类二阶非线性保守系统同宿轨道的显式表达式
本节研究一类具有高次非线性的二阶保守系统(1.10)同宿轨道的显式表示问题.实际上,上述的二阶非线性方程等价于如下平面系统
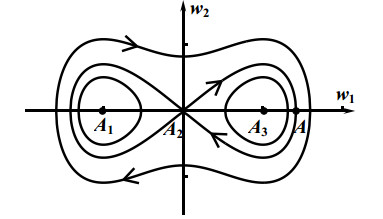
图 2
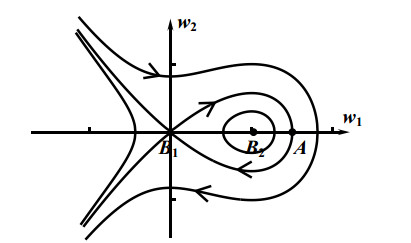
图 3
对方程(1.10)积分一次,可得
这里
经对式(2.3)进行积分计算可得:不管
其中
从而
即
记
可以发现:
对上式进行化简可得
定理2.1 若
其详细推导的初等积分过程见附录3.1.
2.2 Melnikov积分的计算
根据Doelman等的论文[1], Melinkov函数与如下的广义积分有关
然而, Doelman等[1]并没有给出上述积分的计算过程和结果.接下来,基于第2.1节关于同宿轨道的显式表达式
其中
上述结果的详细推导过程见附录3.2.综上,我们有如下结论.
定理2.2 设G-M方程(1.2)具有与Doelman等[1]相同的参数及非线性项等条件,
那么, G-M方程(1.2)具有
注2.1 比较本文得到的(2.7)式与Doelman等[1]的(1.8)式,显然本文得到的结果更为精细.因而,基于本文的结果,关于流的快慢切换的位置能被更为精确地确定.
3 附录
3.1 方程(1.10)同宿轨道的显式表达式初等积分法
上述已指出:但Hamilton量
为简单,先考虑
令
因而
当
令
因而
一般地,当
令
从而
当
令
因此
综上有
我们进一步化简,当
即
所以
又
当
即
因而
又
综上,同宿轨道的显式表达式为
接下来,通过初始条件确定积分常数
3.2 Melnikov积分的计算
记
其中
那么
令
又
从而
进一步地,令
当
考虑如下积分
令
由分部积分,当
当
综上
利用上面结果可以计算出
因为Melnikov积分为
其中
参考文献
Large stable pulse solutions in reaction-diffusion equations
DOI:10.1512/iumj.2001.50.1873 [本文引用: 13]
Dynamics of pulse solutions in Gierer-Meinhardt model with time dependent diffusivity
DOI:10.1016/j.jmaa.2017.08.027
Stable spike clusters for the one-dimensional Gierer-Meinhardt system
Pulses in a Gierer-Meinhardt equation with a slow nonlinearity
Existence, stability, and dynamics of ring and near-ring solutions to the saturated Gierer-Meinhardt model in the semistrong regime
Nonlinear asymptotic stability of the semistrong pulse dynamics in a regularized Gierer-Meinhardt model
DOI:10.1137/050646883 [本文引用: 1]
Geometric singular perturbation theory for ordinary differential equations
DOI:10.1016/0022-0396(79)90152-9 [本文引用: 1]