一类广义Gierer-Meinhardt方程多脉冲同宿解的再研究

数学物理学报 ›› 2019, Vol. 39 ›› Issue (6): 1365-1375.

一类广义Gierer-Meinhardt方程多脉冲同宿解的再研究

朱昆¹,沈建和^1,^2,*()

¹ 福建师范大学数学与信息学院福州 350117
² 福建省分析数学及其应用重点实验室福州 350117

收稿日期:2018-05-03 出版日期:2019-12-26 发布日期:2019-12-28
通讯作者: 沈建和 E-mail:jhshen@fjnu.edu.cn
基金资助:
国家自然科学基金(11771082);福建省教育厅新世纪杰青项目

A Revisit on Multiple-Pulse Homoclinic Solutions in a Generalized Gierer-Meinhardt Equation

Kun Zhu¹,Jianhe Shen^1,^2,*()

¹ College of Mathematics and Informatics, Fujian Normal University, Fuzhou 350117
² Fujian Key Laboratory of Mathematical Analysis and Applications, Fujian Normal University, Fuzhou 350117

Received:2018-05-03 Online:2019-12-26 Published:2019-12-28
Contact: Jianhe Shen E-mail:jhshen@fjnu.edu.cn
Supported by:
the NSFC(11771082);the Program for New Century Excellent Talents in Fujian Province University

摘要/Abstract

摘要：

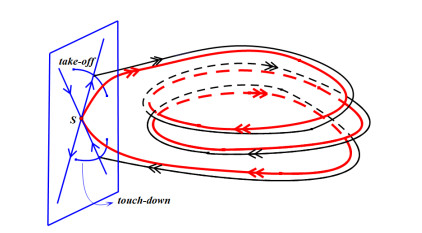
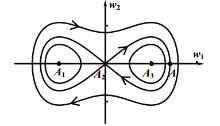
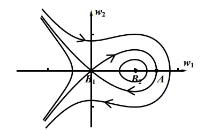
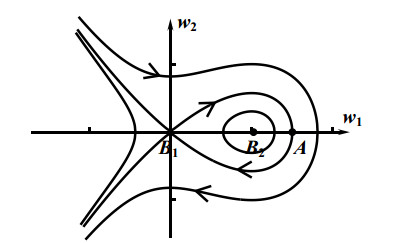
关于广义Gierer-Meinhardt（G-M）方程多脉冲同宿轨道，Doelman等[Indiana Univ Math J，2001，50：443-507]已进行了详细的研究，获得了存在性和稳定性及其参数条件.然而，在上述Doelman等的工作中，Melnikov积分（度量层系统的临界流形的稳定和不稳定流形的横截相交性）并没有计算.因此，该文的工作有两个方面：首先，通过初等积分法，计算获得一类与层系统相关的二阶非线性保守方程同宿轨道的显式表达式；接着，基于该显式表达式，对Melnikov积分进行详细的计算，从而获得上述广义G-M方程存在多脉冲同宿轨道的更为精细的参数条件.

关键词: 广义G-M方程, 多脉冲同宿轨道, Melnikov函数

Abstract:

In paper[1] (Indiana Univ Math J, 2001, 50:443-507), the authors studied the existence and stability of multiple-pulse homoclinic solutions in a generalized Gierer-Meinhardt equation. However, in this paper, a general integral measuring the distance of the stable and unstable manifolds of the critical manifold of the layer system, i.e., the Melnikov integral, was not computed explicitly. So we have two aims in this manuscript. Firstly, we give an elementary method to solve a second-order nonlinear conservative system and hence obtain the explicit representation of the homoclinic orbit. Secondly, we substitute the explicit representation of the homoclinic orbit into the the Melnikov integral. By computing such a general integral, we obtain a more explicitly parametric condition on the existence of multiple-pulse homoclinic solutions in such a generalized Gierer-Meinhardt equation.

Key words: Generalized Gierer-Meinhardt equation, Multi-pulse homoclinic orbit, Melnikov function

中图分类号:

O175.12

朱昆,沈建和. 一类广义Gierer-Meinhardt方程多脉冲同宿解的再研究[J]. 数学物理学报, 2019, 39(6): 1365-1375.

Kun Zhu,Jianhe Shen. A Revisit on Multiple-Pulse Homoclinic Solutions in a Generalized Gierer-Meinhardt Equation[J]. Acta mathematica scientia,Series A, 2019, 39(6): 1365-1375.

图/表 3

参考文献 8

1	Doelman A , Gardner R A , Kaper T J . Large stable pulse solutions in reaction-diffusion equations. Indiana Univ Math J, 2001, 50: 443- 507 doi: 10.1512/iumj.2001.50.1873
2	Nec Y . Dynamics of pulse solutions in Gierer-Meinhardt model with time dependent diffusivity. J Math Anal Appl, 2018, 457 (1): 585- 615 doi: 10.1016/j.jmaa.2017.08.027
3	Wei J , Winter M . Stable spike clusters for the one-dimensional Gierer-Meinhardt system. European J Appl Math, 2017, 28 (4): 576- 635 doi: 10.1017/S0956792516000450
4	Veerman F , Doelman A . Pulses in a Gierer-Meinhardt equation with a slow nonlinearity. SIAM J Appl Dyn Syst, 2013, 12 (1): 28- 60 doi: 10.1137/120878574
5	Moyles I R , Ward M . Existence, stability, and dynamics of ring and near-ring solutions to the saturated Gierer-Meinhardt model in the semistrong regime. SIAM J Appl Dyn Syst, 2017, 16 (1): 597- 639 doi: 10.1137/16M1060327
6	Doelman A , Kaper T J , Promislow K . Nonlinear asymptotic stability of the semistrong pulse dynamics in a regularized Gierer-Meinhardt model. SIAM J Math Anal, 2007, 38 (6): 1760- 1787 doi: 10.1137/050646883
7	Fenichel N . Geometric singular perturbation theory for ordinary differential equations. J Differential Equations, 1979, 31 (1): 53- 98 doi: 10.1016/0022-0396(79)90152-9
8	Jones C. Geometric Singular Perturbation Theory//Johnson R. Dynamical Systems, Montecatibi Terme, Lecture Notes in Mathematics Volume 1609. Berlin: Springer-Verlag, 1994

[1]	廖暑芃, 沈建和. 一类带有慢变参数的sine-Gordon方程的单脉冲异宿轨道[J]. 数学物理学报, 2018, 38(4): 810-822.
[2]	梁海华, 陈玉明, 岑秀丽. 一类拟齐次多项式中心的极限环分支[J]. 数学物理学报, 2018, 38(1): 1-9.