1 引言
对话(dialogue)是群体解决复杂问题的一个重要手段[1].对话模型是对群体对话过程的形式化描述,它不仅是从修辞学角度研究群体对话规律的工具,还是计算机辅助群体研讨支持系统[2]和基于辩论的多Agent交互系统[3]的理论基础.一个好的对话模型不仅能刻画日常对话实际,还能很好地支持对话过程引导和共识提取.Walton和Krabbe[4]从对话初始状态、群体共同目标和个体目标三个因素将对话分为信息索取(information seeking)[5-6]、问询(inquiry)[7]、劝说(persuasion)[8]、谈判(negotiation)[9-11]和协商(deliberation)[12]等五种.目前对前四种对话建模的研究已有很多,但对协商对话建模的研究很少[13].协商对话的目标是探寻群体共同行动方案,如“我们一起到哪里旅游?”、“面对气候变暖,我们的对策是什么?”等.群体成员在协商对话过程中利益目标一致,责任共担,不存在谈判对话中的利益分割问题.协商对话一般要经过确定问题、提出方案和对方案进行论证等三个阶段,其中提出方案是群体发散思维,而对方案进行论证是群体收敛思维.在协商对话之初,个体思维有限,有的还没有形成自己的方案,通过协商对话可以激活思维,促进方案的形成;而在协商对话后期,则要对众多方案进行论证,促进思维收敛,以便形成最终的为群体共同接受的方案.在协商对话过程中,参与者都是以谨慎、探寻和反省的态度与其他参与者交换意见[14],而不是以击败对手为目标,在发言中往往会用“肯定”、“可能”、“不可能”等模态词,因而协商对话中存在一些不确定性信息.协商对话中每个主体虽然没有自己的个体目标,但有自己的信念,因而在协商过程中仍然存在矛盾和冲突,即在协商对话过程中会引发劝说对话[15],通过辩论推理使问题得到论证[8].因此,协商对话模型需要描述从发散到收敛的群体思维过程,并引入不确定性推理及辩论推理方法,其内容包括发言信息结构化分解、对话推演过程表示及争议评价算法等.
现有辩论模型大多只描述了协商对话过程中的某个阶段或某部分信息,没有提供对协商对话过程的全面刻画.例如Toulmin模型[16]重在对论证结构的描述,但没有描述对话交互过程.基于问题的信息系统(Issue-based Information System, IBIS)模型[17]描述了针对问题提出方案并给出方案的理由的决策过程,但没有表示对方案的多层论证结构.Dung的抽象辩论框架[18]描述了争议之间的攻击关系,但它把争议抽象为一个节点而忽略争议的文本内容或内部结构,且没有考虑争议之间的攻击强度,不能反映日常协商对话的全部内容.目前协商对话模型大多建立在以上模型的基础之上,或对它们进行整合,或对它们进行扩展.如Carneades模型[19]对Dung的抽象辩论框架进行扩展,采用Toulmin模型对争议进行结构化分解,但它没有描述协商对话过程中的提出方案阶段,只适合于对劝说对话的建模.Gordon等[20]提出的Zeno模型是一个完整可计算IBIS模型,它允许对问题进行特化和泛化,并通过增加对争议节点的优先序关系确定争议的可接受性,但没有考虑针对方案的多层论证结构.Karacapilidis等[21]的HERMES系统、Baroni等[22-23]的QuAD模型、Liu等[24-25]的基于模糊集的协商模型都是建立在IBIS模型基础之上,它们一方面对IBIS模型进行简化,不考虑对问题的特化和泛化等衍生处理,同时增加对方案的多层论证结构和争议评价量化计算,但它们都没有对争议进行结构化分解,不能反映协商对话的完整逻辑关系.目前针对多Agent协商对话的研究也有一些,但这些研究大多针对对话协议,而对争议的量化及评价没有提出相应方法[14-15].在国内,谭俊峰等[26]提出了树型研讨信息组织模型,该模型描述了发言节点间的语义关系,但没有描述节点之间反对或支持的强度.陈俊良等[27]以IBIS模型和Toulmin模型为基础,建立了一种可对发言进行评价的研讨模型,并提出了一种基于语言加权集结(LWA)算子和节点归约的发言节点评价方法,其工作是对Liu等[24-25]的基于模糊集的协商模型的改进,以语言评价代替模糊数,但并没有克服Liu等[24-25]的方法存在的问题.
针对以上问题,本文提出一种基于IBIS模型的协商对话框架(Deliberation Dialogue Framwork, DDF),先对IBIS模型进行简化处理,不考虑对问题的特化、泛化等衍生处理,然后用可信度因子表示争议前提的不确定性和争议的论证强度.为了确定方案可信度值,提出一种基于模糊Petri网的共识评价方法,用模糊Petri网对DDF进行重构,将模糊争议映射为变迁,将争议前提和结论映射为库所,用托肯值表示陈述的可信度值,通过矩阵迭代运算求解各库所的托肯值,得出最终的协商对话结果.
2 基本IBIS模型
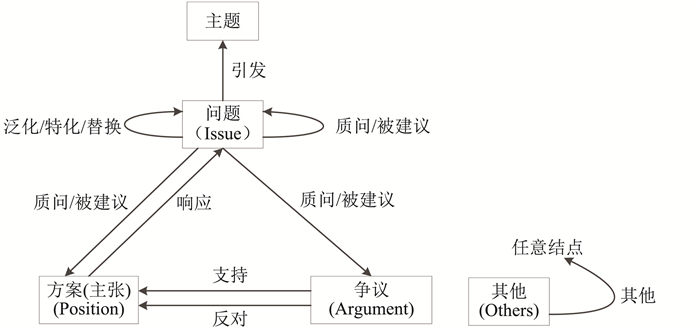
IBIS模型[28]由Horst Rittel提出,主要目的是用图形化方法对采用对话式论证方法求解结构不良问题的过程进行描述,在工程设计、城市规划、政治决策等领域有广泛应用.IBIS模型的基本元素有3种节点和9种边.3种节点分别是问题(Issue)、方案(Position)和争议(Argument). 9种边分别是:方案对问题的响应(Responds-to),争议针对方案支持(Supports-to)或反对(Objects-to);一个问题针对另一个问题的泛化(Generalize)或特化(Specialize)或替换(Replaces),一个问题针对另一个问题或方案或争议的质问(Question)或被建议(Be-suggested-by)、作为回避机制的与其他节点的链接(Other)等,如图 1所示.另外还有主题、事实和模型等3个其他元素.一个基于IBIS模型的完整辩论系统则由问题库、事实库、模型库、主题列表、问题论证映射和文件系统等组成.
图 1
IBIS模型的论证过程如下:
(1)参与者针对主题提出问题,并标识问题与方案的管理指标;
(2)编辑问题,并确定与其他问题的联系;
(3)提出解决问题的方案,并为每个方案提供一个争议表,这些争议来自于提出者与其反对者之间的争论;
(4)从文件系统中检索出针对问题的证据和意见,并将新找到的文献添加到文件系统中;
(5)更新问题-方案-争议映射图;
(6)问题要么通过产生一个可接受方案得到解决,要么需要从专家那里得更多的证据,要么方案受到质问和被建议而引发一个新的问题.
IBIS模型是对复杂问题决策过程的全面刻画,既考虑了针对方案的论证,又考虑了问题的泛化、特化和替换等处理,并对决策过程中需要的数据和支撑资料提供支持.IBIS模型主要针对政策决策问题,早期采用手动方式组织和管理决策.但它存在以下问题:一是没有提出方案可接受性的标准,不能自动得出协商结果;二是没有考虑发言信息的可信度,也没有考虑争议的论证强度;三是由于允许对问题进行泛化、特化、替换等多种处理,同时允许针对问题、方案和争议通过质问和被建议而衍生出新的问题,而且对问题的衍生没有限制,增加了问题的组织和管理难度.这些不足使IBIS模型在计算机系统中的实现面临困难.
3 协商对话框架
协商对话框架建立在IBIS基础之上,即对IBIS模型进行约简、扩展和量化.约简是指只针对单一问题进行协商,不考虑问题的泛化、特化和替换等处理,这样处理的目的是使该模型便于在计算机系统中实现.扩展是指增加对争议的结构化表示,并增加针对方案的多层论证结构.为了体现协商对话的特点,增加对争议前提不确定性和争议论证强度的量化表示.
协商是通过对话进行的[4],对话的基本单元是发言.按照发言的目的,可以把发言分为以下4种类型: 1)针对问题提出方案; 2)对方案或其他发言进行论证; 3)提出质询; 4)回答质询等.其中提出质询不增加任何决策信息,而回答质询可以看作是对前一发言的补充.除此之外,协商对话模型中不考虑与决策无关的其他发言信息.这样所有发言都应该是针对问题或之前的其他发言的响应,整个协商对话将形成一棵以问题为根的树形结构.
定义1 (Statement) 陈述是对事物的肯定性描述,它是发言的基本组成单位.设有两陈述
定义2 (Issue) 问题是协商对话的对象,整个协商对话只针对一个问题,记为
本定义是对IBIS模型进行简化,即不考虑由问题、方案和争议衍生出来的其他问题.
定义3 (Position) 方案是问题求解的备选答案,所有方案的集合记为
定义4 (Argument) 有明确主张和相应根据的发言称为争议.争议可以表示为一个二元组
如果一个争议只有一个前提
争议可以转换成产生式规则:
ⅰ)只有一个前提的争议:
ⅱ)有多个前提的争议:
本定义是对IBIS模型进行扩展,即对争议进行结构化处理,支持多个前提对一个结论的论证.
在实际协商对话中,争议具有不确定性.可以用模糊争议来表示这种不确定性.
定义5 (Fuzzy Argument) 模糊争议是一个四元组
其中
对于前提
本定义是对IBIS模型进行量化,有了量化就可以计算方案的共识值,并依共识值确定方案的可接受性.
定义6 (Dialogue) 设有两个争议
定义7 (Deliberation Dialogue Framework) 协商对话框架是一个4元组:
协商对话框架可以用一个图表示(如图 2所示).图中矩形表示陈述,圆圈表示争议.由争议指向陈述的带箭头的连线表示争议与陈述之间的论证关系,这里的陈述是争议的结论.连接陈述与争议的无向边表示陈述对争议的支持关系,这里的陈述是争议的前提.
图 2
陈述分问题、方案和一般陈述3类,一般陈述可以作为争议的前提,也可以作为争议的结论.方案只能作为方案争议的前提.问题只能作为方案争议的结论.
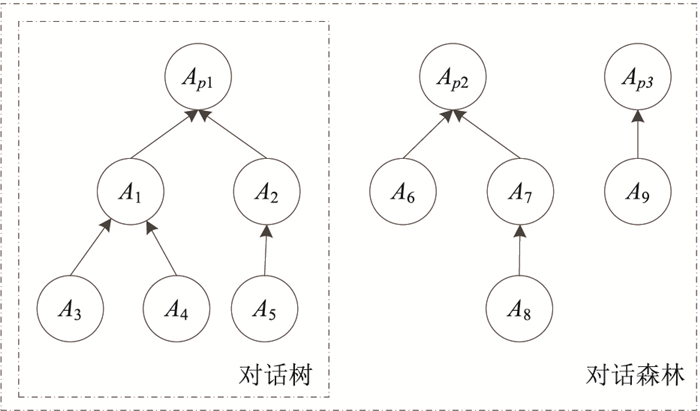
IBIS模型对方案的论证只有一层,因而无法实现对论证的论证.对IBIS模型的扩展的关键是增加对方案的多重论证,即辩论结构,这样就形成了一个以方案争议为根的对话树.如果针对问题提出多个方案,则产生多个对话树,从而构成对话森林.
定义8 (Dialogue Tree) 对话树是有
定义9 (Dialogue Forest)
图 3
4 基于模糊Petri网的共识评价方法
协商对话框架只是描述了对话过程,但并不能确定哪个方案是可接受的,因此接下来需要对方案的可接受性进行计算.本文采用模糊Petri网对协商对话框架进行映射,并提出求方案共识值的算法,最后根据方案的共识值确定方案的可接受性.
4.1 将协商对话框架映射为模糊Petri网
Petri网是一种图形化系统建模工具[29],适合描述具有并发或并行行为的系统.模糊Petri网是对普通Petri网的模糊化.与普通Petri网相比,模糊Petri网的变迁是否点火取决于变迁的阈值
在模糊Petri网运行之前,先进行初始化,即给每个库所赋予一个正实数,称为库所的托肯值.运行时,先计算变迁的各输入弧的输入强度.一个变迁的一个输入弧的输入强度由函数
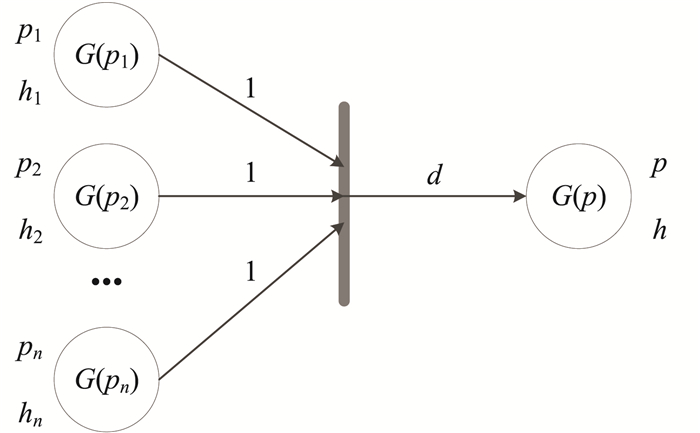
协商对话与基于模糊Petri网的逻辑推理有相似之处,可以将协商对话框架映射为模糊petri网.映射方法是将争议的前提和结论映射为库所,将模糊争议映射为变迁,将陈述可信度映射为库所的托肯值,将争议论证强度映射为变迁到输出库所的连接强度.为了简单起见,输入库所到变迁的连接强度统一定为1.将模糊争议映射为变迁是映射过程的关键.可以先将模糊争议转换为模糊产生式规则,再将模糊产生式规则映射为变迁.设有模糊争议
其对应的模糊petri网如图 4所示.
图 4
定义10 (Deliberation Mapping) 协商对话框架可以转换为模糊Petri网,该Petri网称为协商对话模糊Petri网(Fuzzy Petri Net for Deliberation, FPND). FPND是一个7元组:
当变迁的总输入量
(1)变迁的各输入弧上的输入量与输入库所的托肯值一致,不再另设输入量,即
(2)变迁点火后,只改变变迁输出库所的托肯值,而输入库所的托肯值不变,即不执行
4.2 FPND中托肯值的计算
FPND是随着对话的进行而逐步构造起来的,新产生的争议所对应的变迁的输出库所是被响应争议所对应的变迁的一个输入库所,如果新产生的变迁点火,则会引起前一变迁的输入库所的托肯值的更新,这种更新进而传递到根节点.与基于模糊Petri网的逻辑推理不同[30],非叶子争议节点的前提对应的库所的初始托肯值不为0,因而变迁点火后需要对响应链上的库所托肯值进行合成,这种合成一直要传递到根节点.因而FPND中托肯值的计算包括托肯值合成和托肯值传递两个方面.
4.2.1 托肯值合成计算
设有模糊争议
每个输入弧的输入强度为
变迁点火后,变迁的输出库所的托肯值将发生变化.其计算方法为:
首先计算该库所的所有输入弧的输入量,如果该库所的第
由于
然后将库所
当库所
最后进行托肯值合成:将库所
该公式的一个重要性质是保证了合成后库所的托肯值的取值范围为
4.2.2 基于矩阵迭代运算的托肯值更新算法
一个新的争议产生后,从该争议到根争议的响应链上的所有库所的托肯值都要更新,我们采用矩阵迭代运算对托肯值的更新进行计算.
(1)
(2)
(3)
(4)
算子定义如下:
(1)连接算子
(2)行最小算子
(3)比较算子
(4)集结算子
(5)合成算子
假设有
INPUT:协商对话模糊Petri网(FPND),包括输入矩阵
OUTPUT:各库所的托肯值.
设
STEP 1.计算各变迁输入弧的输入强度,
STEP 2.计算各变迁的总输入量:
STEP 3.将变迁输入量与变迁阈值比较,得到各变迁的有效总输入量:
STEP 4.计算变迁点火后各输出库所的输入量:
STEP 5.计算变迁点火后各库所的托肯值的增加量:
STEP 6.计算当次迭代后各库所的托肯值:
STEP 7.用
4.2.3 算法讨论
托肯值更新函数Token-revision的迭代次数与对话树的高度相同,当迭代到根节点时,所有库所的托肯值将不再发生变化.假设对话树的高度为
协商对话结果是方案所对应的库所的托肯值,这个结果称为方案共识值.方案共识值的取值范围为
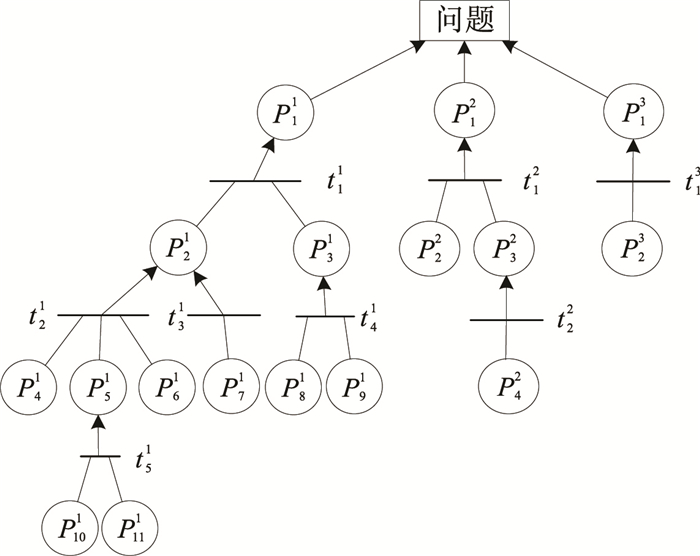
5 实例分析
图 5
表 1 协商对话框架的初始值
| 变迁 | 输入库所 | 输出库所 | 变迁可信度 | 输入库所托肯值 |
| 0.9 | 0.5, 0.9 | |||
| 0.8, 0.9, 0.7 | ||||
| 0.8 | 0.6 | |||
| 0.7, 0.6 | ||||
| 0.6, 0.8 | ||||
| 0.7 | 0.8, 0.3 | |||
| 0.5 | ||||
| 0.5 | 0.5 |
假设所有变迁的点火阈值都0,具体计算如下:
(1)针对方案
1)输入矩阵为:
2)输出矩阵为:
3)变迁阈值向量为:
4)库所初始托肯值向量为:
第一次迭代:
STEP 1.计算各变迁输入弧的输入强度,
STEP 2.计算各变迁的总输入量:
STEP 3.将变迁输入量与变迁阈值比较,得到各变迁的有效总输入量:
STEP 4.计算变迁点火后各库所的输入强度:
STEP 5.计算变迁点火后各库所的托肯值的增加量:
STEP 6.计算本次迭代后各库所的托肯值:
第二次迭代后:
第三次迭代后:
以后库所托肯值不再发生变化,最后得到
(2)针对方案
第二次迭代的结果为:
以后库所托肯值不再发生变化,最后得到
(3)针对方案
对应
在本例中,
在方案
在方案
表 2 托肯值变化表
| 时间节点 | |||||||
| 0 | - | - | - | 0.5 | 0.9 | 0.9 | 0.3 |
| 1 | 0.45 | 0.21 | 0.4 | 0.3558 | 0.468 | 0.522 | 0.18 |
| 2 | 0.3202 | 0.126 | 0.4 | 0.5096 | 0.468 | 0.522 | 0.18 |
| 3 | 0.4212 | 0.126 | 0.4 | 0.5096 | 0.468 | 0.522 | 0.18 |
6 结论
协商对话框架是对协商对话过程的全面刻画,包括争议的结构化分解、争议之间的关系表示,并有相应的争议评价算法.与劝说和谈判对话不同的是,协商对话需要引入不确定性信息表示及处理.协商对话过程中也存在个体信念不一致现象,需要嵌入劝说对话成份,即需要引入辩论推理.本文提出的模型能满足以上要求.一是将争议分解为若干前提和一个结论组成的可废止规则,反映了争议的内部论证结构.二是对IBIS模型进行约简和扩展,使之不仅能表示协商对话实际,同时有利于争议评价计算.约简是指限制问题的泛化和特化,只对单一问题求解;扩展是指增加对方案的多层论证结构,将整个协商对话过程建模成一个对话森林,其中每棵对话树的根节点对应一个方案.三是增加了争议前提和争议的论证强度的量化表示,提出一种基于模糊Petri网的共识评价方法,通过矩阵迭代运算求出方案的最终共识值,算法合理高效.本文方法已用于计算机辅助研讨支持系统中,取得较好的效果.如果要应用于多Agent交互系统中,则还需要做进一步的工作,包括发言信息符号化、Agent信念表示及信念库构建、争议产生方法及对话协议等.
参考文献
从群体支持系统到创造力支持系统
DOI:10.3321/j.issn:1000-6788.2006.05.008 [本文引用: 1]
From group support system to creativity support system
DOI:10.3321/j.issn:1000-6788.2006.05.008 [本文引用: 1]
Case-based strategies for argumentation dialogues in agent societies
Argumentation semantics for defeasible logic
DOI:10.1093/logcom/14.5.675 [本文引用: 1]
Representing epistemic uncertainty by means of dialectical argumentation
DOI:10.1023/A:1016757315265 [本文引用: 1]
Bipolarity in argumentation graphs:Towards a better understanding
DOI:10.1016/j.ijar.2013.03.001 [本文引用: 1]
Coherence and flexibility in dialogue games for argumentation
Argumentation-based inference and decision making -A medical perspective
DOI:10.1109/MIS.2007.102 [本文引用: 1]
Deliberation dialogues for reasoning about safety critical actions
DOI:10.1007/s10458-011-9174-5 [本文引用: 1]
The eightfold way of deliberation dialogue
On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games
The Carneades model of argument and burden of proof
Computer supported argumentation and collaborative decision making:the HERMES system
Automatic evaluation of design alternatives with quantitative argumentation
A computational argumentation methodology for capturing and analyzing design rationale arising from multiple perspectives
综合集成研讨厅中的研讨信息组织模型
DOI:10.3321/j.issn:1000-6788.2005.01.013 [本文引用: 1]
A group argumentation information-structuring model in hall for workshop of metasynthetic engineering
DOI:10.3321/j.issn:1000-6788.2005.01.013 [本文引用: 1]
基于IBIS和Toulmin辩论形式的群体研讨模型
Group argumentation model based on IBIS and Toulmin's argument schema
Petri nets:Properties, analysis and applications
Dynamic representation of fuzzy knowledge based on fuzzy petri net and genetic-particle swarm optimization