奇异摄动问题作为应用数学密切关注的研究对象之一^[1],广泛存在于流体力学^[2]、大气等离子体^[3]、生物和生态^[4]等实际问题中.在这些奇异摄动问题中,有些问题往往涉及到多个小参数,如下列齐次线性方程的初值问题

(1.1) $\begin{eqnarray}\label{60} \left\{\begin{array}{ll} \epsilon x''+\mu ax+bx=0, \, \ 0<t<1, \\ x(0)=1, \, \ x'(0)=0, \end{array}\right. \end{eqnarray} $

其中, $a, \, \ b$为正常数,而$\epsilon, \, \ \mu$为小参数,且当$\mu$趋于零时, $\eta=\epsilon/\mu^{2}$也趋于零.

文献[5]和[6]分别讨论了问题(1.1)渐近解的构造及其极限性态行为.通过分析,问题(1.1)的解在$t=0$附近分别有宽度为$\xi=\mu$和$\xi\eta=\epsilon/\mu$的边界层,并且$\xi\eta$比$\xi$更小.因此,在$t=0$附近有两个层,构成“层中层”,即形成“套层”.换而言之,问题(1.1)在边界层处的时间变化尺度不一样,从而产生不同类型的边界层,即存在快慢层.

本文将研究一类具有快慢层的非光滑奇异摄动问题的空间对照结构,而这类快慢层出现在不同端点的邻域附近内.

考虑如下的奇异摄动方程

(1.2) $\begin{eqnarray}\label{61}\left\{\begin{array}{ll}\epsilon^{4}y''={\rm sgn}(-t)A(y, t)\epsilon y'+B(y, t), \quad -1\leq t\leq 1, \\y(-1, \epsilon)=a, \, \ y(1, \epsilon)=b, \end{array}\right.\end{eqnarray}$

其中, $\epsilon$是小参数, ${\rm sgn}$为符号函数.

令$\epsilon y'=z$,则方程(1.2)可化为等价的方程组

(1.3) $\begin{eqnarray}\label{62}\left\{\begin{array}{ll}\epsilon y'=z, \\\epsilon^{3}z'={\rm sgn}(-t)A(y, t)z+B(y, t), \\y(-1, \epsilon)=a, \, \ y(1, \epsilon)=b.\end{array}\right.\end{eqnarray}$

先提出下列假设.

假设1.1  函数$A(y, t)$、$ B(y, t)$在$D=\{(y, t):|y|\leq l, \, \ -1\leq t\leq 1\}$上充分光滑,其中$l$是给定的正实数.

假设1.2  函数$A(y, t)$满足$A(y, t)>0$.退化方程$B(y, t)$有两个孤立根$\varphi_{i}(t), \, \ i=1, 2$.不妨令$\varphi_{1}(t)<\varphi_{2}(t)$,并且满足不等式

$B_{y}(\varphi_{i}(t), t)>0 \, \ (i=1, 2).$

在上述的假设下,方程(1.3)在区间$[-1, 1]$上可存在空间对照结构解,而且解在不同端点的邻域附近产生不同类型的边界层.为了得到其对应的光滑渐近解,在$t=0$处将方程(1.3)分成左右两个问题.

左问题: $-1\leq t\leq 0$,

(1.4) $\begin{eqnarray}\label{63}\left\{\begin{array}{ll}\epsilon y'^{(-)}=z^{(-)}, \\\epsilon^{3}z'^{(-)}=A(y^{(-)}, t)z^{(-)}+B(y^{(-)}, t), \\y^{(-)}(-1, \epsilon)=a, \, \ y^{(-)}(0, \epsilon)=p(\epsilon).\end{array}\right.\end{eqnarray}$

右问题: $0\leq t\leq 1$,

(1.5) $\begin{eqnarray}\label{64}\left\{\begin{array}{ll}\epsilon y'^{(+)}=z^{(+)}, \\\epsilon^{3}z'^{(+)}=-A(y^{(+)}, t)z^{(+)}+B(y^{(+)}, t), \\y^{(+)}(0, \epsilon)=p(\epsilon), \, \ y^{(+)}(1, \epsilon)=b, \end{array}\right.\end{eqnarray}$

其中, $p(\epsilon)=p_{0}+\epsilon p_{1}+\epsilon^{2}p_{2}+\cdots$. $p_{i}$为待定常数,由下面的光滑性条件(1.6)来确定.

(1.6) $\begin{eqnarray}\label{65}y'^{(-)}(0, \epsilon)=y'^{(+)}(0, \epsilon).\end{eqnarray}$

在上述的假设下,此时左问题(1.4)在$t=-1$的邻域附近出现慢层(时间变化尺度为$1/\epsilon$),在$t=0$的邻域附近则出现快层(时间变化尺度为$1/\epsilon^{3}$).而右问题(1.5)在$t=0$的邻域附近出现快层(时间变化尺度为$1/\epsilon^{3}$),在$t=1$的邻域附近出现慢层(时间变化尺度为$1/\epsilon$).因此,根据边界层函数法^[7],构造问题(1.3)如下形式的渐近解

$y(t, \epsilon)=\bar{y}^{(\mp)}(t, \epsilon)+Ly(\tau, \epsilon)+Q^{(\mp)}y(\tau_{0}, \epsilon)+Ry(\tau_{1}, \epsilon), $

$ z(t, \epsilon)=\bar{z}^{(\mp)}(t, \epsilon)+Lz(\tau, \epsilon)+Q^{(\mp)}z(\tau_{0}, \epsilon)+Ry(\tau_{1}, \epsilon), $

其中, $\tau=\frac{t+1}{\epsilon}$, $\tau_{0}=\frac{t}{\epsilon^{3}}$, $\tau_{1}=\frac{t-1}{\epsilon}$.

正则部分$\bar{x}^{(\mp)}(t, \epsilon)$,左边界层部分$L{x}(\tau, \epsilon)$以及右边界层部分$R{x}(\tau_{1}, \epsilon)$具有相同的渐近展开式,即有如下形式

(2.1) $ \begin{equation}\label{68} \bar{x}^{(\mp)}(t, \epsilon)=\bar{x}_{0}^{(\mp)}(t)+\epsilon \bar{x}_{1}^{(\mp)}(t)+\epsilon^{2}\bar{x}_{2}^{(\mp)}(t)+\cdots, \end{equation}$

(2.2) $ \begin{equation}\label{69} Lx(\tau, \epsilon)=L_{0}x(\tau)+\epsilon L_{1}x(\tau)+\epsilon^{2}L_{2}x(\tau)+\cdots, \end{equation}$

(2.3) $\begin{equation}\label{610} Rx(\tau_{1}, \epsilon)=R_{0}x(\tau_{1})+\epsilon R_{1}x(\tau_{1})+\epsilon^{2}R_{2}x(\tau_{1})+\cdots, \end{equation}$

这里$x=(y, z)^{T}$.但不同的是,此时内部层部分$Q^{(\mp)}y(\tau_{0}, \epsilon)$和$Q^{(\mp)}z(\tau_{0}, \epsilon)$的渐近展式却不一样,分别为

(2.4) $ \begin{equation}\label{611} Q^{(\mp)}y(\tau_{0}, \epsilon)=Q_{0}^{(\mp)}y(\tau_{0})+\epsilon Q_{1}^{(\mp)}y(\tau_{0})+\epsilon^{2}Q_{2}^{(\mp)}y(\tau_{0})+\cdots, \end{equation}$

(2.5) $ \begin{equation}\label{612} Q^{(\mp)}z(\tau_{0}, \epsilon)=\epsilon^{-2}Q_{-2}^{(\mp)}z(\tau_{0})+\epsilon^{-1}Q_{-1}^{(\mp)}z(\tau_{0})+Q_{0}^{(\mp)}z(\tau_{0})+\cdots. \end{equation}$

将(2.1)-(2.5)式分别代入上述相应的左问题和右问题中,通过分离变量并比较$\epsilon$的同次幂系数,则可确定渐近解级数各项系数所需的方程和定解条件.

(1)正则级数(2.1)各项系数的确定.

确定主项$\bar{y}_{0}^{(\mp)}(t)$和$\bar{z}_{0}^{(\mp)}(t)$所满足的方程

$ \begin{eqnarray}\label{613} \left\{\begin{array}{ll} \bar{z}_{0}^{(\mp)}(t)=0, \\ A^{(\mp)}(\bar{y}_{0}^{(\mp)}(t), t)\bar{z}_{0}^{(\mp)}(t)+B(\bar{y}_{0}^{(\mp)}(t), t)=0, \end{array}\right.\nonumber \end{eqnarray} $

其中, $A^{(-)}=A, \, \ A^{(+)}=-A$.这里讨论的是从$\varphi_{1}(t)$到$\varphi_{2}(t)$的解,即取$\bar{y}_{0}^{(\mp)}(t)=\varphi_{1, 2}(t)$.

确定$\bar{y}_{k}^{(\mp)}(t)$和$\bar{z}_{k}^{(\mp)}(t)$所满足的方程

(2.6) $\begin{eqnarray}\label{616} \left\{\begin{array}{ll} \displaystyle\frac{\rm d}{{\rm d}t}\bar{y}_{k-1}^{(\mp)}=\bar{z}_{k}^{(\mp)}, \\ A^{(\mp)}(\bar{y}_{0}^{(\mp)}, t)\bar{z}_{k}^{(-)}+B_{y}(\bar{y}_{0}^{(\mp)}, t)\bar{y}_{k}^{(\mp)}+f_{k}^{(\mp)}(t)=0, \end{array}\right. \end{eqnarray} $

这里$f_{k}^{(\mp)}(t)$是关于$\bar{y}_{j}^{(\mp)}(t), \, \ \bar{z}_{j}^{(\mp)}(t), \, \ j<k$的复合已知函数.根据假设1.2,可从(2.6)式直接解得

$\begin{eqnarray}\label{617} \bar{z}_{k}^{(\mp)}(t)=\frac{\rm d}{{\rm d}t}\bar{y}_{k-1}^{(\mp)}(t), \, \, \ \bar{y}_{k}^{(\mp)}(t)=-\frac{A^{(\mp)}(\varphi_{1, 2}(t), t)\bar{z}_{k}^{(\mp)}(t)+f_{k}^{(\mp)}(t)}{B_{y}(\varphi_{1, 2}(t), t)}.\nonumber \end{eqnarray} $

这样就确定正则级数(2.1)的所有系数.

(2)左边界层级数(2.2)各项系数的确定.

确定$L_{0}y(\tau), \, \ L_{0}z(\tau)$所满足的方程和定解条件

(2.7) $\begin{eqnarray}\label{618} \left\{\begin{array}{ll} \displaystyle\frac{{\rm d}L_{0}y}{{\rm d}\tau}=L_{0}z, \, \ \bar{A}(\tau)L_{0}z+\bar{B}(\tau)=0, \\ \varphi_{1}(-1)+L_{0}y(0)=a, \, \ L_{0}y(+\infty)=0, \end{array}\right. \end{eqnarray}$

其中, “$\bar{}$ ”表示对应函数在点$(\varphi_{1}(-1)+L_{0}y(\tau), -1)$处的取值.

考虑到假设1.2,方程(2.7)可改写为

(2.8) $\begin{eqnarray}\label{619} \left\{\begin{array}{ll} \displaystyle\frac{{\rm d}L_{0}y}{{\rm d}\tau}=-\frac{\bar{B}(\tau)}{\bar{A}(\tau)}\equiv G(L_{0}y), \\ L_{0}y(0)=a-\varphi_{1}(-1), \, \ L_{0}y(+\infty)=0, \end{array}\right. \end{eqnarray} $

其中,函数$G(L_{0}y)=-B(\varphi_{1}(-1)+L_{0}y(\tau), -1)/A(\varphi_{1}(-1)+L_{0}y(\tau), -1)$.方程(2.8)有平衡点$L_{0}y(\tau)=0$,且该平衡点是渐近稳定的.这是因为

(2.9) $\begin{eqnarray}\label{620} \displaystyle\frac{{\rm d}G(L_{0}y)}{{\rm d} L_{0}y}(0)=-\frac{\bar{B}_{y}\bar{A}-\bar{B}\bar{A}_{y}}{\bar{A}^{2}}\Big|_{L_{0}y=0}<0. \end{eqnarray}$

为了保证问题(2.8)的解$L_{0}y(\tau)$的存在性,还需如下假设.

假设2.1  初值$a-\varphi_{1}(-1)$落在方程(2.8)平衡点$L_{0}y(\tau)=0$的吸引域内.

确定$L_{k}y(\tau), \, \ L_{k}z(\tau)$所满足的方程和定解条件

(2.10) $\begin{eqnarray}\label{621}\left\{\begin{array}{ll}\displaystyle\frac{{\rm d}L_{k}y}{{\rm d}\tau}=L_{k}z, \\\bar{A}(\tau)L_{k}z+[\bar{A}_{y}(\tau)L_{0}z+\bar{B}_{y}(\tau)]L_{k}y+\bar{h}_{k}(\tau)=0, \\\bar{y}^{(-)}_{k}(-1)+L_{k}y(0)=0, \, \ L_{k}y(+\infty)=0, \end{array}\right.\end{eqnarray}$

其中, $\bar{h}_{k}(\tau)$是关于$L_{j}z(\tau)$, $L_{j}y(\tau), \, \ 0\leq j<k$的已知函数.方程(2.10)可写成如下等价的形式

(2.11) $\begin{eqnarray}\label{622}\left\{\begin{array}{ll}\displaystyle\frac{{\rm d}L_{k}y}{{\rm d}\tau}=-\frac{[\bar{A}_{y}(\tau)L_{0}z+\bar{B}_{y}(\tau)]L_{k}y+\bar{h}_{k}(\tau)}{\bar{A}(\tau)}, \\\bar{y}^{(-)}_{k}(-1)+L_{k}y(0)=0, \, \ L_{k}y(+\infty)=0.\end{array}\right.\end{eqnarray}$

从方程(2.11)则可确定$L_{k}y(\tau)$.至此就完全确定的左边界层(2.2)中的每一项系数,而且满足下列估计式.

引理2.1  左边界层函数满足下列不等式

$\begin{eqnarray}\label{623}\mid L_{k}y(\tau) \mid < C{\rm e}^{-\kappa\tau}, \, \ \mid L_{k}z(\tau) \mid < C{\rm e}^{-\kappa\tau}, \, \ \tau\geq0, \nonumber\end{eqnarray}$

其中, $C>0$和$\kappa>0$.

证  当$k=0$时,由方程(2.8)可得

$\displaystyle\frac{{\rm d}L_{0}y}{{\rm d}\tau}=G_{y}(\varphi_{1}(-1)+\theta L_{0}y, -1)L_{0}y, \, \ 0<\theta<1.$

故可解得

$L_{0}y(\tau)=(a-\varphi_{1}(-1)){\rm e}^{\int ^{\tau}_{0}G_{y}(\varphi_{1}(-1)+\theta L_{0}y, -1){\rm d}s}.\nonumber $

结合(2.9)式,所以存在常数$T>0$及$\overline{\kappa}>\underline{\kappa}>0$,使得当$\tau>T$时,有下列不等式成立

$ -\overline{\kappa}< G_{y}(\varphi_{1}(-1)+\theta L_{0}y, -1) <-\underline{\kappa}.$

于是就可得到$L_{0}y(\tau)$的估计式

$ | L_{0}y(\tau)| \leq (| a-\varphi_{1}(-1)| {\rm e}^{\int ^{T}_{0}G_{y}{\rm d}s}){\rm e}^{-\int ^{\tau}_{T}\underline{\kappa}{\rm d}s}, $

则有$| L_{0}y(\tau)|< C{\rm e}^{-\kappa\tau}$.当$k>0$时,则根据(2.11)式可得到结论.

(3)内部层级数(2.4), (2.5)各项系数的确定.

确定主项$Q^{(\mp)}_{0}y(\tau_{0})$和$Q^{(\mp)}_{-2}z(\tau_{0})$的方程和定解条件

(2.12) $ \begin{eqnarray}\label{628} \left\{\begin{array}{ll} \displaystyle\frac{{\rm d}Q^{(\mp)}_{0}y}{{\rm d}\tau_{0}}=Q^{(\mp)}_{-2}z, \\ \displaystyle\frac{{\rm d}Q^{(\mp)}_{-2}z}{{\rm d}\tau_{0}}=A^{(\mp)}(\varphi_{1, 2}(0)+Q^{(\mp)}_{0}y, 0)Q^{(\mp)}_{-2}z, \\ \varphi_{1, 2}(0)+Q^{(\mp)}_{0}y(0)=p_{0}, \, \ Q^{(\mp)}_{0}y(\mp\infty)=0. \end{array}\right. \end{eqnarray} $

作变量替换$\tilde{y}^{(\mp)}=\varphi_{1, 2}(0)+Q^{(\mp)}_{0}y(\tau_{0}), \, \ \tilde{z}^{(\mp)}=Q^{(\mp)}_{-2}z(\tau_{0})$,则方程(2.12)可化为

(2.13) $ \begin{eqnarray}\label{629} \left\{\begin{array}{ll} \displaystyle\frac{{\rm d}\tilde{z}^{(\mp)}}{{\rm d}\tau_{0}}=A^{(\mp)}(\tilde{y}^{(\mp)}, 0)\tilde{z}^{(\mp)}, \, \ \displaystyle\frac{{\rm d}\tilde{y}^{(\mp)}}{{\rm d}\tau_{0}}=\tilde{z}^{(\mp)}, \\ \tilde{y}^{(\mp)}(0)=p_{0}, \, \ \tilde{y}^{(\mp)}(\mp\infty)=\varphi_{1, 2}(0). \end{array}\right. \end{eqnarray} $

故可得确定求$\tilde{y}^{(\mp)}(\tau_{0})$的方程和边值条件

(2.14) $\begin{eqnarray}\label{630} \left\{\begin{array}{ll} \displaystyle\frac{{\rm d}\tilde{y}^{(\mp)}}{{\rm d}\tau_{0}}=\displaystyle\int^{\tilde{y}^{(\mp)}} _{\varphi_{1, 2}(0)}A^{(\mp)}(y, 0){\rm d}y\equiv Y^{(\mp)}(\tilde{y}^{(\mp)}), \\ \tilde{y}^{(\mp)}(0)=p_{0}. \end{array}\right. \end{eqnarray}$

方程(2.14)有衡点$\tilde{y}^{(\mp)}(\tau_{0})=\varphi_{1, 2}(0)$.根据假设1.2,有

$\frac{{\rm d}Y^{(\mp)}}{{\rm d}\tilde{y}^{(\mp)}}(\varphi_{1, 2}(0))=A^{(\mp)}(\varphi_{1, 2}(0), 0)>(<)0.$

同样地,从方程(2.14)可得

$ \tilde{z}^{(\mp)}(0)=\int ^{p_{0}}_{\varphi_{1, 2}(0)}A^{(\mp)}(y, 0){\rm d}y.$

根据光滑性条件(1.6),可得

$ Q^{(+)}_{-2}z(0)=Q^{(+)}_{-2}z(0), \, \ Q^{(-)}_{-1}z(0)=Q^{(+)}_{-1}z(0).\nonumber$

即得确定$p_{0}$的表达式为

(2.15) $\begin{eqnarray}\label{649}\tilde{I}(p_{0})=\int^{p_{0}}_{\varphi_{2}(0)}A(y, 0){\rm d}y+\int^{p_{0}}_{\varphi_{1}(0)}A(y, 0){\rm d}y=0, \end{eqnarray}$

引理2.2  在区间$(\varphi_{1}(0), \varphi_{2}(0))$上,方程(2.15)有唯一解$p_{0}$.

证  根据

$\tilde{I}(\varphi_{1}(0))\tilde{I}(\varphi_{2}(0))=-\bigg(\int^{\varphi_{2}(0)}_{\varphi_{1}(0)}A(y, 0){\rm d}y\bigg)^{2}<0. \nonumber$

故由介值定理得,存在$p_{0}\in (\varphi_{1}(0), \varphi_{2}(0))$,使得$\tilde{I}(p_{0})=0$.又$\tilde{I}'(p_{0})=2A(p_{0}, 0)>0$.故$p_{0}$是唯一的.

确定了参数$p_{0}$,通过相平面分析法可知,方程(2.14)解是存在的.至此就完全确定了内部层级数的主项部分.

确定$Q^{(\mp)}_{k}y(\tau_{0})$和$Q^{(\mp)}_{k-2}z(\tau_{0})$的方程和定解条件

(2.16) $\begin{eqnarray}\label{638}\left\{\begin{array}{ll}\displaystyle\frac{{\rm d}Q^{(\mp)}_{k}y}{{\rm d}\tau_{0}}=Q^{(\mp)}_{k-2}z, \\\displaystyle\frac{{\rm d}Q^{(\mp)}_{k-2}z}{{\rm d}\tau_{0}}=\tilde{A}^{(\mp)}Q^{(\mp)}_{k-2}z+\tilde{A}^{(\mp)}_{y}Q_{-2}^{(\mp)}zQ_{k}^{(\mp)}y+\tilde{h}^{(\mp)}_{k}(\tau_{0}), \\Q^{(\mp)}_{k}y(0)=p_{k}-\bar{y}_{k}^{(\mp)}(0), \, \ Q^{(\mp)}_{k}y(\mp\infty)=0, \end{array}\right.\end{eqnarray}$

其中, “$\tilde{}$”表示对应函数在点$(\varphi_{1, 2}(0)+Q^{(\mp)}_{0}y(\tau_{0}), 0)$处的取值, $\tilde{h}^{(\mp)}_{k}(\tau_{0})$为已知的复合函数.从方程(2.16)可计算得

(2.17) $\begin{eqnarray}\label{639}Q^{(-)}_{k-2}z(0)=A^{(\mp)}(p_{0}, 0)[p_{k}-\bar{y}_{k}^{(\mp)}(0)]+\int^{0}_{\mp\infty}\tilde{h}^{(\mp)}_{k}(\tau_{0}){\rm d}\tau_{0}.\end{eqnarray} $

由光滑性条件(1.6),可得

(2.18) $\begin{eqnarray}\label{647}\bar{z}^{(-)}_{k-2}(0)+ Q^{(-)}_{k-2}z(0)=\bar{z}^{(+)}_{k-2}(0)+ Q^{(+)}_{k-2}z(0), \, \ k\geq2.\end{eqnarray}$

从(2.17)和(2.18)式,得到

$\begin{eqnarray*}\label{651}&&\bar{z}^{(-)}_{k-2}(0)+ A(p_{0}, 0)[p_{k}-\bar{y}_{k}^{(-)}(0)]+\int^{0}_{-\infty} \tilde{h}^{(-)}_{k}(\tau_{0}){\rm d}\tau_{0}\\&=&\bar{z}^{(+)}_{k-2}(0)- A(p_{0}, 0)[p_{k}-\bar{y}_{k}^{(+)}(0)]+\int^{0}_{+\infty} \tilde{h}^{(+)}_{k}(\tau_{0}){\rm d}\tau_{0}, \nonumber\end{eqnarray*}$

解得

$p_{k}=\frac{H+\bar{z}_{k-2}^{(+)}(0)-\bar{z}_{k-2}^{(-)}(0)+A(p_{0}, 0)(\bar{y}_{k}^{(-)}(0)-\bar{y}_{k}^{(+)}(0))}{2A(p_{0}, 0)}, \nonumber$

其中

$H=\int^{0}_{+\infty} \tilde{h}^{(+)}_{k}(\tau_{0}){\rm d}\tau_{0}-\int^{0}_{-\infty} \tilde{h}^{(-)}_{k}(\tau_{0}){\rm d}\tau_{0}.\nonumber$

这样内部层级数(2.4), (2.5)的各项系数就确定了,且满足以下估计式.

引理2.3  内部层函数满足下列不等式

$\mid Q^{(\mp)}_{k}y(\tau_{0}) \mid < C{\rm e}^{-\kappa\mid\tau_{0}\mid}, \, \ \mid Q^{(\mp)}_{k-2}z(\tau_{0}) \mid < C{\rm e}^{-\kappa\mid\tau_{0}\mid}, \nonumber$

其中, $C>0$和$\kappa>0$.

(4)右边界层级数(2.3)各项系数的确定

确定$R_{0}y(\tau), \, \ R_{0}z(\tau)$所满足的方程和定解条件

(2.19) $\begin{eqnarray}\label{641}\left\{\begin{array}{ll}\displaystyle\frac{{\rm d}R_{0}y}{{\rm d}\tau}=R_{0}z, \, \ -\hat{A}(\tau_{1})R_{0}z+\hat{B}(\tau_{1})=0, \\\varphi_{2}(1)+R_{0}y(0)=b, \, \ R_{0}y(-\infty)=0, \end{array}\right.\end{eqnarray}$

其中, “$\hat{}$ ”表示对应函数在点$(\varphi_{2}(1)+R_{0}y(\tau_{1}), 1)$处的取值.

根据假设1.2,方程(2.19)可改写为

(2.20) $\begin{eqnarray}\label{642} \left\{\begin{array}{ll} \displaystyle\frac{{\rm d}R_{0}y}{{\rm d}\tau_{1}}=\frac{\hat{B}(\tau_{1})}{\hat{A}(\tau_{1})}\equiv D(R_{0}y), \\ R_{0}y(0)=b-\varphi_{2}(1), \, \ R_{0}y(-\infty)=0. \end{array}\right. \end{eqnarray} $

方程(2.20)有平衡点$R_{0}y(\tau_{1})=0$,且该平衡点是渐近不稳定的.这是因为

$\displaystyle\frac{{\rm d}D(R_{0}y)}{{\rm d} R_{0}y}(0)=\frac{\hat{B}_{y}\hat{A}-\hat{B}\hat{A}_{y}}{\hat{A}^{2}}\Big|_{R_{0}y=0}>0.\nonumber $

为确保问题(2.20)的解$R_{0}y(\tau_{1})$的存在性,还需下列假设.

假设2.2  初值$b-\varphi_{2}(1)$落在方程(2.20)平衡点$R_{0}y(\tau_{1})=0$的影响域内.

确定$R_{k}y(\tau_{1}), \, \ R_{k}z(\tau_{1})$所满足的方程和定解条件

(2.21) $\begin{eqnarray}\label{644}\left\{\begin{array}{ll}\displaystyle\frac{{\rm d}R_{k}y}{{\rm d}\tau_{1}}=R_{k}z, \\-\hat{A}(\tau_{1})R_{k}z+[-\hat{A}_{y}(\tau_{1})R_{0}z+\hat{B}_{y}(\tau_{1})]R_{k}y+\hat{h}_{k}(\tau_{1})=0, \\\bar{y}^{(+)}_{k}(1)+R_{k}y(0)=0, \, \ R_{k}y(-\infty)=0, \end{array}\right.\end{eqnarray}$

其中, $\hat{h}_{k}(\tau_{1})$是关于$R_{j}z(\tau_{1})$, $R_{j}y(\tau_{1}), \, \ 0\leq j<k$的已知函数.故由(2.21)式则可确定出$R_{k}y(\tau_{1})$.这样就确定了右边界层部分的每一项系数,且满足下列估计.

引理2.4  右边界层函数满足下列不等式

$\begin{eqnarray}\label{645}\mid R_{k}y(\tau_{1}) \mid < C{\rm e}^{\kappa\tau_{1}}, \, \ \mid R_{k}z(\tau_{1}) \mid < C{\rm e}^{\kappa\tau_{1}}, \, \ \tau_{1}\leq0, \nonumber\end{eqnarray}$

其中, $C>0$和$\kappa>0$.

注2.1  针对左问题(1.4),作变量替换$\tau=\frac{t-t_{0}}{\epsilon^{\alpha}}$,则方程(1.4)可化为

(2.22) $\begin{eqnarray}\label{6300}\left\{\begin{array}{ll}\epsilon^{1-\alpha} \displaystyle\frac{\rm d}{{\rm d}\tau}y^{(-)}=z^{(-)}, \\\epsilon^{3-\alpha}\displaystyle\frac{\rm d}{{\rm d}\tau}z^{(-)}=A(y^{(-)}, t)z^{(-)}+B(y^{(-)}, t).\end{array}\right.\end{eqnarray}$

通过消去方程(2.22)中的第一个和第二个方程最高阶导数前的$\epsilon$,则有$\alpha=1$和$\alpha=3$.故左问题(1.4)在边界邻域附近内出现的时间变化尺度为$1/\epsilon$和$1/\epsilon^{3}$.

当$\alpha=1$时,左问题(1.4)的附加方程为

(2.23) $\begin{eqnarray}\label{6301} \left\{\begin{array}{ll} \displaystyle\frac{\rm d}{{\rm d}\tau}y^{(-)}=z^{(-)}, \\ A(y^{(-)}, t)z^{(-)}+B(y^{(-)}, t)=0. \end{array}\right. \end{eqnarray} $

类似于(2.7)式的讨论,方程(2.23)有平衡点$y^{(-)}=\varphi_{1}(t)$,且该平衡点是渐近稳定的.因此,在$t=-1$的邻域附近出现慢层(时间变化尺度为$1/\epsilon$).

当$\alpha=3$时,考虑到$\epsilon$的奇异性,则左问题(1.4)的附加方程为

(2.24) $ \begin{eqnarray}\label{6302} \left\{\begin{array}{ll} \displaystyle\frac{\rm d}{{\rm d}\tau}y^{(-)}=z^{(-)}, \\ \displaystyle\frac{\rm d}{{\rm d}\tau}z^{(-)}=A(y^{(-)}, t)z^{(-)}. \end{array}\right. \end{eqnarray}$

类似于(2.12)式的讨论,方程(2.24)有平衡点$y^{(-)}=\varphi_{1}(t)$,且该平衡点是渐近不稳定的.因此,在$t=0$的邻域附近出现快层(时间变化尺度为$1/\epsilon^{3}$).

利用“缝接法”^[8]证明问题多尺度渐近解的存在性.令

$\begin{eqnarray}\tilde{p}(\epsilon)=p_{0}+\epsilon p_{1}+\epsilon^{2}p_{2}+\cdots+\epsilon^{n}(p_{n}+\delta).\nonumber\end{eqnarray}$

作差值函数

$L(\tilde{p}, \epsilon)=\epsilon[\frac{\rm d}{{\rm d}t}y^{(-)}(0, \epsilon)-\frac{\rm d}{{\rm d}t}y^{(+)}(0, \epsilon)]. $

考虑到多尺度渐近解的构造,则有

$ \begin{eqnarray*} L(\tilde{p}, \epsilon)&=&\epsilon[\displaystyle\frac{\rm d}{{\rm d}t}y^{(-)}(t_{0}, \epsilon)-\displaystyle\frac{\rm d}{{\rm d}t}y^{(+)}(t_{0}, \epsilon)]\nonumber\\ &=&\epsilon^{n}[\bar{z}^{(-)}_{n}(0)+ Q^{(-)}_{n}z(0)-\bar{z}^{(+)}_{n}(0)- Q^{(+)}_{n}z(0)]+O(\epsilon^{n+1})\nonumber\\ &=&2\epsilon^{n}A(p_{0}, 0)\delta+O(\epsilon^{n+1}).\nonumber \end{eqnarray*} $

可见,当$\epsilon$充分小,并且取$\delta$为异号值时, $L(\tilde{p}, \epsilon)$也异号,所以由介值定理,存在$p^{\ast}\in [p_{n}-\delta, p_{n}+\delta]$,使得$L(p^{\ast}, \epsilon)=0$.

将上述对问题(1.2)所得到的光滑渐近解归结为如下的定理.

定理3.1  在假设1.1、1.2、2.1和2.2下,则存在充分小的$\epsilon_{0}$.当$0<\epsilon<\epsilon_{0}$时,问题(1.2)的光滑解$y(t, \epsilon)$存在,且具有如下的渐近表达式和估计

$ y(t, \epsilon)=\left\{\begin{array}{ll} \displaystyle\sum\limits_{i=0}^{n}\epsilon^{i}[\bar{y}_{i}^{(-)}(t)+L_{i}y(\tau)+Q_{i}^{(-)}y(\tau_{0})]+O(\epsilon^{n+1}), \, \ &-1\leq t\leq 0, \\ \displaystyle\sum\limits_{i=0}^{n}\epsilon^{i}[\bar{y}_{i}^{(+)}(t)+Q_{i}^{(+)}y(\tau_{0})+R_{i}y(\tau_{1})]+O(\epsilon^{n+1}), \, \ &0\leq t\leq1. \end{array}\right.$

考虑如下的奇异摄动方程

(4.1) $\begin{eqnarray}\label{6102}\left\{\begin{array}{ll}\epsilon^{4}y''={\rm sgn}(-t)\epsilon y'+(y-1-t^{2})(y+1+t^{2}), \\y(-1, \epsilon)=-2, \, \ y(1, \epsilon)=2.\end{array}\right.\end{eqnarray}$

根据本文的算法,方程(4.1)的左问题的正则部分的主项为$\bar{y}_{0}^{(-)}(t)=-1-t^{2}$,而边界层部分的主项分别满足如下方程

(4.2) $ \begin{eqnarray}\label{11618} \left\{\begin{array}{ll} \displaystyle\frac{{\rm d}L_{0}y}{{\rm d}\tau}=L_{0}z, \, \ L_{0}z+L_{0}y(L_{0}y-4)=0, \\ L_{0}y(0)=0, \, \ L_{0}y(+\infty)=0\end{array}\right. \end{eqnarray}$

和

(4.3) $ \begin{eqnarray}\label{11628} \left\{\begin{array}{ll} \displaystyle\frac{{\rm d}Q^{(-)}_{0}y}{{\rm d}\tau_{0}}=Q^{(-)}_{-2}z, \, \ \displaystyle\frac{{\rm d}Q^{(-)}_{-2}z}{{\rm d}\tau_{0}}=Q^{(-)}_{-2}z, \\ Q^{(-)}_{0}y(0)=p_{0}+1, \, \ Q^{(-)}_{0}y(-\infty)=0. \end{array}\right. \end{eqnarray} $

解方程(4.2)和(4.3)可得

$ L_{0}y(\tau)=0, \, \ Q^{(-)}_{0}y(\tau_{0})=(p_{0}+1){\rm e}^{\tau_{0}}, $

这里, $\tau=(t+1)/\epsilon$及$\tau_{0}=t/\epsilon^{3}$.

对于方程(4.1)的右问题,同样有

$\bar{y}_{0}^{(+)}(t)=1+t^{2}, \, \ Q^{(+)}_{0}y(\tau_{0})=(p_{0}-1){\rm e}^{-\tau_{0}}, \, \ R_{0}y(\tau_{1})=0.$

从表达式(2.15),则可知$p_{0}=0$.故方程(4.1)的零次渐近解为

$\left\{\begin{array}{ll} y^{(-)}=-1-t^{2}+{\rm e}^{\tau_{0}}, \\ y^{(+)}=1+t^{2}-{\rm e}^{-\tau_{0}}. \end{array}\right.\nonumber $

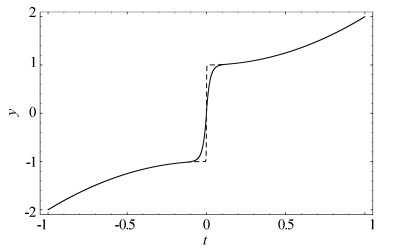
因此,方程(4.1)存在如图 1所示的空间对照结构解.