自1982年,越来越多的学者关注到Hopfield神经网络,其在分类、联想记忆、并行计算和优化中的应用日益广泛.这类应用强烈依赖于网络的动力行为.大量的学者们研究了Hopfield神经的一些动力学行为并取得了可观的成果.例如,文献[1-9]研究了分支和混沌现象, [10-12]研究了周期解, [13-19]讨论了平衡点的稳定性.

值得一提的是, Lyapunov稳定性^[13-19]指的是平衡点的稳定性,此稳定性的前提条件是平衡点存在.但有时在许多真实的物理系统中,平衡点并不存在.因此,一些学者开始研究具有时滞的神经网络的吸引集^[20-27].在文献[20]中验证了,在全局吸引集之外,不存在平衡点、周期性状态和几乎周期性的混沌状态.在文献[27]中针对不同时滞范围的系统给出了原点吸引范围的估计.

众所周知,不等式是一种研究微分方程的重要的技术工具,见文献[28-37].但是,对于一类具有变时滞的非线性和非自治的神经型Hopfield神经网络,研究其渐近行为时,上述参考文献中的不等式是无效的.我们将给出一个积分不等式,用它来研究上述模型的全局吸引集的存在性.

本文的结构如下.首先是预备知识,包括一些必要的定义、假设以及引理.第3部分讨论模型的全局吸引集.第4部分列举例验证主要结果.第5部分给出结论.

本文中, $E_n$表示$n\times n$维单位矩阵. ${\Bbb R} $是实数集, ${\Bbb R} _+=[0, +\infty)$,符号${\Bbb R} ^n$表示$n$维Euclidean空间. $A$是一个方阵, $A^{-1}$为其逆矩阵, $\rho(A)$是其谱半径. $A \leq B (A<B)$表示矩阵$A$和$B$中对应元素均满足$\leq (<)$的不等式关系.如果$ A \geq 0$,则$A$称为一个非负矩阵.所有从拓扑空间$X$到拓扑空间$Y$的连续映射构成空间$C(X, Y)$.对于$x\in {\Bbb R} ^n, \varphi \in C [(-\infty, t_0], {\Bbb R} ^n]$在$ (-\infty, t_0]$上有界, $\tau(t) \in C({\Bbb R} , {\Bbb R} _+)$,我们定义

$ \begin{eqnarray} &&|x|=(|x_1|, \cdots , |x_n|), \;\;\;\;\parallel x(t) \parallel_{\tau(t)}=(\parallel x_1(t) \parallel_{\tau(t)}, \parallel x_2(t) \parallel_{\tau(t)}, \cdots , \parallel x_n(t) \parallel_{\tau(t)}), \nonumber\\ &&\parallel x_i(t) \parallel_{\tau(t)}=\sup\limits_{0 \leq s \leq \tau(t)}|x_i(t-s)|.\nonumber \end{eqnarray}$

我们考虑如下具有变时滞的神经型Hopfield神经网络模型

(2.1) $ \begin{eqnarray} &&{\dot{x}_{i}(t)}=-a_{i}(t)x_{i}(t)+\sum^{n}_{j=1}b_{ij}(t)f_j(x_{j}(t)) +\sum^{n}_{j=1}c_{ij}(t)f_j(\dot{x}_{j}(t-\tau(t))) +I_i(t), \end{eqnarray} $

模型(2.1)由一元神经域$F_x$构成,其中$x_i(t)$是$F_x$中第$i$个神经元的激活, $a_{i}(t)\geq 0$表示被动衰变率, $b_{ij}(t)$和$c_{ij}(t)$分别代表各自的神经元权重系数. $f_j$是激活函数, $I_i$是外部输入. $\tau(t) \in C({\Bbb R} , {\Bbb R} _+)$是传输延迟, $ \lim\limits_{t\rightarrow +\infty }(t-\tau(t))=+\infty$, ${\dot{\tau}(t)}\leq \tau <1$,其中$\tau$是常数.

系统(2.1)的初始条件是$x_i(s)=\varphi_i(s)$, $s \in (-\infty, t_0]$, $i=1, 2, \cdots, n, $其中$\varphi_i(\cdot)$定义在$(-\infty, t_0]$上的实值连续函数.

我们定义如下符号

$ \begin{eqnarray} && a(t)={\rm diag}\{a_1(t), a_2(t), \cdots, a_n(t)\}, \;\;\;\;b(t)=(b_{ij}(t))_{n \times n} , \;\;\;\;c(t)=(c_{ij}(t))_{n \times n}, \nonumber\\ && B(t)=(|b_{ij}(t)|)_{n \times n}, \;\;C(t)=(|c_{ij}(t)|)_{n \times n}, \;\;\bar{I}(t)=(|I_1(t)|, |I_2(t)|, \cdots, |I_n(t)|)^T. \nonumber \end{eqnarray}$

为了方便进一步讨论,我们给出如下假设,定义及重要引理.

(A1)对任意$x_{j}\in {\Bbb R} $, $j \in {\Bbb N}$,存在常数$l_j\geq 0$,使得成立

$|f_j(x_j)|\leql_j|x_j|, \;\;\;L={\rm diag}\{l_1, l_2, \cdots, l_n\}.\nonumber$

(A2)对$ t\geq t_0$, $\forall s \geq t_0$,存在常数矩阵$\Sigma \geq 0$,使得成立

${\rm e}^{-\int_{s}^t a(v){\rm d}v}C(s)L \leq \Sigma.$

(A3)对$ t\geq t_0$,存在非负常数矩阵$\Pi$和常数向量$I \geq 0$,使得成立

$\int_{t_0}^t {\rm e}^{-\int_{s}^t a(v){\rm d}v}B(s)L {\rm d}s \leq \Pi, \;\;\;\;\int_{t_0}^t {\rm e}^{-\int_{s}^t a(v){\rm d}v}\bar{I}(s){\rm d}s\leq I.$

(A4) $\bar{\Pi}\triangleq \Sigma/(1-\tau)+\Pi \geq 0$, $\rho(\bar{\Pi}) \leq 1$.

(A5)对某些$\theta >0$,有$k_i \triangleq \inf\limits_{t_0 \leq s \leq t}\int_{s}^{s+\theta}a_i(v){\rm d}v >0$, $i=1, 2, \cdots, n.$

定义2.1  如果对任意常数$\varepsilon>0$, $t_0 \geq 0$,存在常数$\delta(\varepsilon)>0$,使得对所有$t \geq t_0$, $\parallel x(t, t_0, \varphi) \parallel \leq \varepsilon$及$\sup\limits_{t_0 -\tau \leq s \leq t_0}\parallel \varphi(s) \parallel<\delta(\varepsilon)$成立,则称系统(2.1)关于局部状态$x(t)$一致有界.

定义2.2  如果存在一个紧集$\Omega \subset {\Bbb R} ^n$,对任意初始值$\varphi \in C [(-\infty, t_0], {\Bbb R} ^n] $,成立

$\limsup\limits_{t \rightarrow +\infty}d(x(t), \Omega)=0, $

其中$x(t)=x(t, t_0, \varphi)$, $d(x(t), \Omega)$表示在${\Bbb R} ^n$中$x(t)$到$\Omega$的距离,则称$\Omega$为系统(2.1)的全局吸引集.

定义2.3  如果系统(2.1)是一致有界并且有一个全局吸引集$\Omega$,则称其为Lagrange稳定.

定义2.4^[28]  设$f \in C({\Bbb R} _+, {\Bbb R} _+)$,对任意给定的$\eta$和任意$\varepsilon >0$,存在常数$\beta$, $T$和$\alpha$,使得,对任意$ t \geq \alpha, $下式成立

$\int_\eta^t f(s){\rm d}s \leq \beta, \;\;\;\int_\eta^{t-T} f(s){\rm d}s \leq \varepsilon, $

则称$f(t, s) \in UC_t$.

引理2.1^[37]  对任意非负矩阵$A \geq 0$,如果$\rho(A)<1$,则$(E-A)^{-1}\geq 0$.

引理2.2  令$G(t, t_0) \in C({\Bbb R} \times {\Bbb R} , {{\Bbb R} _+^n})$, $B \in {{\Bbb R} _+^{n \times n}}$, $Q(t, s) \in C({\Bbb R} \times {\Bbb R} , {{\Bbb R} _+^{n \times n}})$, $I=(i_1, i_2, \cdots, i_n)^T \geq 0$, $\varphi(t) \in C((-\infty, t_0], {{\Bbb R} _+^n})$, $\alpha_1$是常数, $x(t) \in C({\Bbb R} , {{\Bbb R} _+^n})$是如下时滞积分不等式的一个解

(2.2) $\begin{eqnarray} && x(t)\leq G(t, t_0)+B{{\parallel x(t)\parallel}_ {\tau(t)}} +\int_{\alpha_1}^t {Q(t, s){\parallel x(s)\parallel}_{\tau(s)}{\rm d}s}+I, \nonumber\\ && x(t)\leq \varphi(t), \;\;\;\;\;\;\;\;\;\;\;\; t\neq t_0. \end{eqnarray} $

若满足如下条件

(ⅰ) $G \triangleq \sup_{t_0 \leq s \leq +\infty}G(s, t_0)$,存在常数非负矩阵$P$满足对$t \geq t_0, $有

(2.3) $\begin{eqnarray} \int_{\alpha_1}^t Q(t, s){\rm d}s \leq P .\end{eqnarray}$

(ⅱ) $\bar P=P+B$, $\rho(\bar P)<1$.

则存在常数向量$M>0$,使得对于$t \geq t_0, $有

(2.4) $\begin{eqnarray}\;\;x(t)<(E_n-\bar P)^{-1}(M+I).\end{eqnarray}$

证  由条件(ⅱ)和引理2.1, $(E_n-\bar P)^{-1}$存在并且$(E_n-\bar P)\geq 0.$由此存在一个常数向量$\bar G >G$,使得

$\varphi(t)<(E_n-\bar P)^{-1}M, \;\;\;\; \forall t \in (-\infty, t_0].$

假设(2.3)式不成立,则一定存在一个常数$t_1>t_0$和一些整数$\alpha \in \{1, 2, \cdots, n\}$使得

(2.5) $x_{\alpha}(t_1)=\{(E_n-\bar P)^{-1}(M+I)\}_{\alpha}, $

(2.6) $x(t)\leq (E_n-\bar P)^{-1}(M+I), t \leq t_1, $

其中$\{\cdot \}_i$表示向量$\{\cdot \}$的第$i$个元素.

不失一般性,我们假设存在一个常数$t_1$, $t_0<t_1$,及一些整数$\alpha$满足(2.5)和(2.6)式.

考虑到表达式(2.2), (2.4)和$G(t_1, t_0)<M$,可得

(2.7) $\begin{eqnarray}x_{\alpha}(t_1) & \leq & \{G(t_1, t_0)+B \parallel x(t_1)\parallel_{\tau(t_1)} +\int_{\alpha_1}^{t_1}Q(t, s)\parallel x(s)\parallel_{\tau(s)}{\rm d}s+I\}_{\alpha}\nonumber\\ \nonumber & < &\{M+[B+\int_{\alpha_1}^{t_1}Q(t, s){\rm d}s](E_n-\barP)^{-1}(M+I)+I\}_{\alpha}\\ \nonumber & \leq & \{M+[B+P](E_n-\barP)^{-1}(M+I)+I\}_{\alpha}\\ \nonumber & = & \{M+\bar P(E_n-\barP)^{-1}(M+I)+I\}_{\alpha}\\ \nonumber & = & \{(\bar P(E_n-\barP)^{-1}+E_n)(M+I)\}_{\alpha}\\ \nonumber & = & \{(E_n-\barP)^{-1}(\bar P+(E_n-\bar P)E_n)(M+I)\}_{\alpha}\\ & = &\{(E_n-\bar P)^{-1}(M+I)\}_{\alpha}, \end{eqnarray}$

这与等式(2.5)矛盾,因此不等式(2.3)成立.证明完毕.

注2.1  与文献[28-33]中的积分不等式相比较,引理2.2中的时滞积分不等式更适用于神经型Hopfield神经网络模型.

定理3.1  假设(A1)-(A4)成立,则系统(2.1)一致有界.

证  由条件(A1),对任意$ t \geq t_0$,有

$ \begin{eqnarray*} |x_i(t)| & \leq & {\rm e}^{-\int_{t_0}^t a_i(v){\rm d}v}|\varphi_i(t_0)|+\int_{t_0}^t {\rm e}^{-\int_s^t a_i(v){\rm d}v}\sum^{n}_{j=1}|b_{ij}(s)|l_j \parallel x_j(s)\parallel _{\tau(s)}{\rm d}s\\ &&+\int_{t_0}^t {\rm e}^{-\int_s^t a_i(v){\rm d}v} \sum^{n}_{j=1}|c_{ij}(s)|l_j | \dot{x}_j(s-\tau(s)) |{\rm d}s +\int_{t_0}^t {\rm e}^{-\int_s^t a_i(v){\rm d}v}\bar{I}(s){\rm d}s.\end{eqnarray*}$

从而

(3.1) $ \begin{eqnarray} |x(t)| & \leq & {\rm e}^{-\int_{t_0}^t a(v){\rm d}v}|\varphi(t_0)|+\int_{t_0}^t {\rm e}^{-\int_s^t a(v){\rm d}v}B(s)L \parallel x(s)\parallel _{\tau(s)}{\rm d}s \nonumber \\&&+\int_{t_0}^t {\rm e}^{-\int_s^t a(v){\rm d}v}C(s)L | \dot{x}(s-\tau(s))|{\rm d}s +\int_{t_0}^t {\rm e}^{-\int_s^t a(v){\rm d}v}\bar{I}(s){\rm d}s. \end{eqnarray} $

由(A2)可得

(3.2) $ \begin{eqnarray} \int_{t_0}^t {\rm e}^{-\int_s^t a(v){\rm d}v}C(s)L| \dot{x}(s-\tau(s))|{\rm d}s &\leq &\Sigma \int_{t_0}^t| \dot{x}(s-\tau(s))|{\rm d}s \nonumber\\ &\leq& \frac{\Sigma}{1-\tau}(\parallel x(t)\parallel _{\tau(t)}+|\varphi(t_0-\tau(t_0))|). \end{eqnarray} $

由(3.1)和(3.2)式,可得

(3.3) $ \begin{eqnarray} |x(t)| & \leq & {\rm e}^{-\int_{t_0}^t a(v){\rm d}v}|\varphi(t_0)|+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))|+\frac{\Sigma}{1-\tau}\parallel x(t)\parallel _{\tau(t)} \nonumber \\&& +\int_{t_0}^t {\rm e}^{-\int_s^t a(v){\rm d}v}LB(s) \parallel x(s)\parallel _{\tau(s)}{\rm d}s+\int_{t_0}^t {\rm e}^{-\int_s^t a(v){\rm d}v}\bar{I}(s){\rm d}s. \end{eqnarray} $

结合(3.3)式,条件(A3), (A4)和引理2.2,可得存在一个常数向量$K>0$,使得

(3.4) $\begin{eqnarray}|x(t)|<(E_n-\bar{\Pi})^{-1}(\bar{\Pi}+K+I), \;\;\;\; \forall t \geq t_0, \end{eqnarray} $

即系统(2.1)的解关于局部状态$x(t)$一致有界.

注3.1  由(3.4)式易得每个解的分量的有界性.

定理3.2  假设满足(A1)-(A5),则集合

$\Omega=\bigg\{\mu \in {\Bbb R} ^n\bigg{|}|\mu|\leq(E_n-\bar{\Pi})^{-1}(\Pi+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))|+I)\bigg\}$

为系统(2.1)的全局吸引集,即系统(2.1)为全局Lagrange稳定.

证  由定理3.1,存在一个非负常数向量$\delta \in {{\Bbb R} }^n $,使得

(3.5) $\begin{eqnarray}\lim\limits_{t \rightarrow +\infty}\sup |x(t)|=\delta \leq (E_n-\bar\Pi)^{-1}(\Pi+K+I).\end{eqnarray}$

下面我们将证明$\delta \in \Omega$.

由条件(A5)和定义2.4, $ {\rm e}^{-\int_s^t a_i(v){\rm d}v} \in UC_t, \; i=1, 2, \cdots, n$.事实上,取$T=m\theta$,存在整数$n$满足$n\theta \leq t-T-t_0 \leq (n+1) \theta$,可得

(3.6) $\begin{eqnarray}\int_{t_0}^{t-T}{\rm e}^{-\int_s^t a_i(v){\rm d}v}{\rm d}s &\leq&\nonumber \sum\limits_{j=0}^n \int_{t_0+j\theta} ^{t_0+(j+1)\theta}{\rm e}^{-\int_s^t a_i(v){\rm d}v}{\rm d}s \\ &\leq&\nonumber \sum\limits_{j=0}^n \theta {\rm e}^{-\int_{t_0+(j+1)\theta} ^{t_0+(n+m)\theta} a_i(v){\rm d}v}\\ &\leq&\nonumber \theta {\rm e}^{-mk_i}({\rm e}^{k_i}+1+{\rm e}^{-k_i}+\cdots+{\rm e}^{-(n-1)k_i})\\ & \leq &\frac{\theta {\rm e}^{-(m-1){k_i}}}{1-{\rm e}^{-k_i}}. \end{eqnarray} $

当$m=0$,可得

(3.7) $\begin{eqnarray} \int_{t_0} ^{t}{\rm e}^{-\int_s^t a_i(v){\rm d}v}{\rm d}s &=&\nonumber\int_{t_0} ^{t_0+n \theta}{\rm e}^{-\int_s^t a_i(v){\rm d}v}{\rm d}s+ \int_{t_0+n \theta} ^{t }{\rm e}^{-\int_s^t a_i(v){\rm d}v}{\rm d}s \\&\leq&\nonumber \theta(1+{\rm e}^{-k_i}+\cdots+{\rm e}^{-(n-1)k_i})+\theta \\&\leq&\theta+\frac{\theta}{1-{\rm e}^{-k_i}}. \end{eqnarray}$

由(3.6)和(3.7)式,可推得对于$i=1, 2, \cdots, n$,有${\rm e}^{-\int_s^t a_i(v){\rm d}v}\in UC_t$.易得${\rm e}^{-\int_s^t a_i(v){\rm d}v}a_i(s)\in UC_t$, $i=1, 2, \cdots, n$.因此,对于任意$\epsilon>0$和$\varepsilon=(1, 1, \cdots, 1)\in {\Bbb R} ^n$,有正数$A$和常数矩阵$R$,使得对任意$ t>t_0+A$,有

(3.8) $ \begin{equation} {\rm e}^{-\int_{t_0}^t a(v){\rm d}v}|\varphi(t_0)|<\frac{\epsilon\varepsilon}{4}, \;\;\;\; \int_{t-A} ^{t}{\rm e}^{-\int_{s}^t a(v){\rm d}v}{\rm d}s\leq R, \end{equation} $

(3.9) $\begin{equation} \int_{t_0} ^{t-A}{\rm e}^{-\int_{s}^t a(v){\rm d}v}B(s)L(E_n-\bar{\Pi})^{-1}(\Pi+K+I){\rm d}s<\frac{\epsilon\varepsilon}{4}. \end{equation} $

根据上极限的定义和$ \lim\limits_{t \rightarrow +\infty}(t-\tau(t))=+\infty$,存在充分大$t_2\geq {t_0+2A}$,满足

(3.10) $\begin{equation} \parallel x(t) \parallel_{\tau(t)}<\delta+\epsilon\varepsilon, \;\;\;\;t \geq t_2, \end{equation} $

其中$ \tau(t)=2A+\sup\limits_{t-2A\leq s\leq t}\tau(s)$.

因此,结合条件(A3), (3.3)和(3.8)-(3.10)式,可得对任意$ t \geq t_2$,有

$ \begin{eqnarray*} |x(t)| & \leq & \frac{\epsilon\varepsilon}{4}+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))| +\frac{\Sigma}{1-\tau}\parallel x(t)\parallel _{\tau(t)}\\ &&+\int_{t_0}^t {\rm e}^{-\int_s^t a(v){\rm d}v}B(s)L \parallel x(s)\parallel _{\tau(s)}{\rm d}s+I\\ & \leq & \frac{\epsilon\varepsilon}{4}+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))| +\frac{\Sigma}{1-\tau}(\bar{\delta}+\epsilon\bar{\varepsilon})\\ &&+(\int_{t_0}^{t-A}+\int_{t-A}^{t}) {\rm e}^{-\int_s^t a(v){\rm d}v} B(s)L \parallel x(s)\parallel _{\tau(s)}{\rm d}s+I\\ & \leq & \frac{\epsilon\varepsilon}{4}+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))| +\frac{\Sigma}{1-\tau}({\delta}+\epsilon{\varepsilon})\\ &&+\frac{\epsilon\varepsilon}{4}+\int_{t-A}^{t} {\rm e}^{-\int_s^t a(v){\rm d}v} B(s)L \parallel x(s)\parallel _{\tau(s)}{\rm d}s+I\\ & \leq & \epsilon\varepsilon+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))|+\bar{\Pi}({\delta}+\epsilon{\varepsilon})+\Pi+I. \end{eqnarray*}$

再由(3.5)式和上极限定义,存在$t_3\geq t_2$满足$|x(t_3)|>\delta-\epsilon\varepsilon$.则

$\delta-\epsilon\varepsilon<\epsilon\varepsilon+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))| +\bar{\Pi}({\delta}+\epsilon{\varepsilon})+\Pi+I.$

令$\epsilon \rightarrow 0$,可得

$\delta < \bar{\Pi}\delta+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))|+\Pi+I $

和

$\delta < (E_n-\bar{\Pi})^{-1}(\Pi+\frac{\Sigma}{1-\tau}|\varphi(t_0-\tau(t_0))|+I), $

即$\delta \in \Omega.$因此集合$\Omega $为系统(2.1)的全局吸引集,即系统(2.1)为全局Lagrange稳定.

注3.2  显然,如果系统(2.1)有一个全局吸引集,则系统(2.1)的解一致有界.

注3.3  若把平衡点作为吸引集的特殊情况,则Lyapunov稳定为Lagrange稳定的特例.因此,如果系统存在平衡点,定理3.2的结论课用于讨论Lyapunov稳定性.

定理3.3  假设定理3.2的所有条件成立及$I_i(t)=0, i=1, \cdots, n$.则$x(t)=0$为系统(2.1)的平衡点,并且全局渐近稳定.

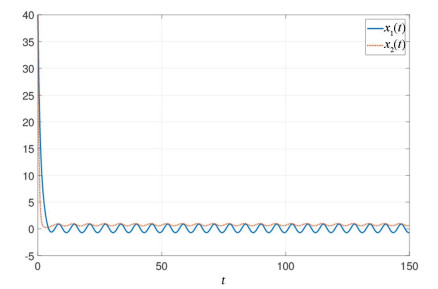
例4.1  考虑如下模型

(4.1) $\begin{eqnarray}\left \{\begin{array}{lll}{\dot{x}_{1}(t)}&=&-x_{1}(t)+0.2165\sin(t) x_{1}(t) +0.2165\cos(t) x_{2}(t)+0.0301\dot{x}_{1}(t-\tau)\\&&+0.1624\dot{x}_{2}(t-\tau)+\sin(t), \\{\dot{x}_{2}(t)}&=&-2x_{2}(t)+0.0005 x_{1}(t)+0.3\dot{x}_{1}(t-\tau)+0.5\dot{x}_{2}(t-\tau)+\arctan(t), \end{array}\right.\end{eqnarray}$

其中$ t \geq 0, $$\tau=0.05$,初始值为$\varphi_1(t)=\varphi_2(t)=40.$显然

$ a(t) = \left(\begin{array}{cc} 1\quad & 0\\ 0\quad& 2 \end{array}\right), \; b(t) = \left(\begin{array}{cc} 0.2165\sin(t)\quad& 0.2165\cos(t)\\ 0.0005\quad&0 \end{array}\right), $

$ B(t) = \left(\begin{array}{cc} 0.2165|\sin(t)|\quad& 0.2165|\cos(t)|\\ 0.0005\quad&0 \end{array}\right), \quadc(t) = \left(\begin{array}{cc} 0.0301 \quad& 0.1624\\ 0.3\quad&0.5 \end{array}\right)=C(t), $

$\bar{I}(t)=(|\sin(t)|, |\arctan(t)|)^T.$经过计算,可得

$\int_{0}^t {\rm e}^{-(t-s)}|\sin (s)|{\rm d}s \leq 0.8660, \quad \int_{0}^t {\rm e}^{-(t-s)}|\cos (s)|{\rm d}s \leq 0.8660, \quad L=E_n, $

${\rm e}^{-\int_{s}^t a(v){\rm d}v}C(s)L \leq \left(\begin{array}{cc} 0.0301\quad & 0.1624\\ 0.3\quad&0.5 \end{array}\right)=\Sigma, $

$\int_{0}^t {\rm e}^{-\int_{s}^t a(v){\rm d}v}B(s)L {\rm d}s \leq \left(\begin{array}{cc} 0.1875 \quad& 0.1875\\ 0.0259\quad& 0.0736 \end{array}\right)=\Pi, $

$\int_{0}^t {\rm e}^{-\int_{s}^t a(v){\rm d}v}\bar{I}(s){\rm d}s\leq \left(\begin{array}{c} 0.8660\\ 0.7854 \end{array}\right)=I, \quad\bar{\Pi}=\left(\begin{array}{cc}0.2191\quad&0.3584 \\ 0.3416 \quad& 0.6\end{array}\right) $

和$\rho(\bar{\Pi})=0.8575<1$.

定理3.2中所有的条件都满足,所以存在$k=\bigg(\begin{array}{c} 0.2857\\ 0.4 \end{array}\bigg), $使得

$\Omega=\bigg\{(x_1, x_2)^T \in {{\Bbb R} }^2 \bigg{|} \left(\begin{array}{c} |x_1|\\|x_2|\end{array}\right) \leq \left(\begin{array}{c} 35.8354\\68.2936\end{array}\right) \bigg\}$

为系统(4.1)的全局吸引集.

基于积分不等式和非负矩阵的性质,考虑了变时滞神经型Hopfield神经网络模型,得到了保证系统Lagrange稳定和全局吸引集的充分条件.并且,本文的方法可以用来研究平衡点的全局渐近稳定性.