具有变时滞的神经型Hopfield神经网络的全局吸引子研究

数学物理学报 ›› 2019, Vol. 39 ›› Issue (4): 823-831.

具有变时滞的神经型Hopfield神经网络的全局吸引子研究

周庆华¹,万立^2,*(),刘杰²

¹ 肇庆学院数学与统计学院广东肇庆 526061
² 武汉纺织大学数学与计算机学院武汉 430073

收稿日期:2018-04-01 出版日期:2019-08-26 发布日期:2019-09-11
通讯作者: 万立 E-mail:wanlinju@aliyun.com
基金资助:
国家自然科学基金(11501499);国家自然科学基金(61573011);国家自然科学基金(11301403);国家自然科学基金(61304022);国家自然科学基金(11271295);广东省自然科学基金(2015A030313707)

Global Attracting Set for Neutral Type Hopfield Neural Networks with Time-Varying Delays

Qinghua Zhou¹,Li Wan^2,*(),Jie Liu²

¹ School of Mathematics and Statistics, Zhaoqing University, Guangdong Zhaoqing 526061
² College of Mathematics and Computer Sciences, Wuhan Textile University, Wuhan 430073

Received:2018-04-01 Online:2019-08-26 Published:2019-09-11
Contact: Li Wan E-mail:wanlinju@aliyun.com
Supported by:
the NSFC(11501499);the NSFC(61573011);the NSFC(11301403);the NSFC(61304022);the NSFC(11271295);the Natural Science Foundation of Guangdong Province(2015A030313707)

摘要/Abstract

摘要：

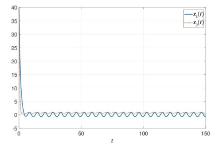
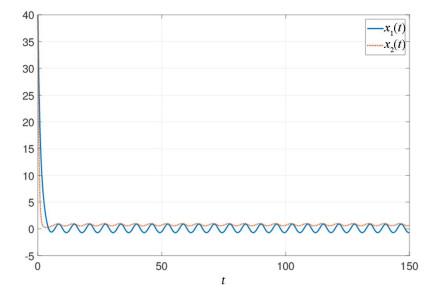
该文探讨了一类具有变时滞的非线性及非自治的神经型Hopfield神经网络的渐近性质.利用非负矩阵的性质和矩阵不等式，得到了保证该系统全局吸引集存在和Lagrange稳定性的充分条件.最后，给出一个例子说明理论的有效性.

关键词: 神经型Hopfield神经网络, 变时滞, Lagrange稳定, 全局吸引集, 积分不等式

Abstract:

This paper deals with the asymptotic properties of a class of nonlinear and nonautonomous neutral type Hopfield neural networks with time-varying delays. By applying the property of nonnegative matrix and an integral inequality, some sufficient conditions are derived to ensure the existence of the global attracting set and the stability in a Lagrange sense for the considered system. Finally, an example is given to demonstrate the effectiveness of our theoretical result.

Key words: Neutral-type Hopfield neural networks, Time-varying delays, Lagrange stability, Global attracting set, Integral inequality

中图分类号:

O193

周庆华,万立,刘杰. 具有变时滞的神经型Hopfield神经网络的全局吸引子研究[J]. 数学物理学报, 2019, 39(4): 823-831.

Qinghua Zhou,Li Wan,Jie Liu. Global Attracting Set for Neutral Type Hopfield Neural Networks with Time-Varying Delays[J]. Acta mathematica scientia,Series A, 2019, 39(4): 823-831.

图/表 1

参考文献 37

1	Huang Y , Yang X S . Hyperchaos and bifurcation in a new class of four-dimensional Hopfield neural networks. Neurocomputing, 2006, 69: 1787- 1795 doi: 10.1016/j.neucom.2005.11.001
2	He W , Cao J . Stability and bifurcation of a class of discrete-time neural networks. Appl Math Model, 2007, 31: 2111- 2122 doi: 10.1016/j.apm.2006.08.006
3	Huang W , Huang Y . Chaos of a new class of Hopfield neural networks. Appl Math Comput, 2008, 206: 1- 11
4	Kaslik E , Balint St . Bifurcation analysis for a discrete-time Hopfield neural network of two neurons with two delays and self-connections. Chaos Soliton Fract, 2009, 39: 83- 91 doi: 10.1016/j.chaos.2007.01.126
5	Zheng P S , Tang W S , Zhang J X . Some novel double-scroll chaotic attractors in Hopfield networks. Neurocomputing, 2010, 73: 2280- 2285 doi: 10.1016/j.neucom.2010.02.015
6	Marichal R L , Gonzalez E J , Marichal G N . Hopf bifurcation stability in Hopfield neural networks. Neural Netw, 2012, 36: 51- 58 doi: 10.1016/j.neunet.2012.09.007
7	Mazrooei-Sebdani R , Farjami S . Bifurcations and chaos in a discrete-time-delayed Hopfield neural network with rings tructures and different internal decays. Neurocomputing, 2013, 99: 154- 162 doi: 10.1016/j.neucom.2012.06.007
8	Akhmet M , Fen M . Generation of cyclic/toroidal chaos by Hopfield neural networks. Neurocomputing, 2014, 145: 230- 239 doi: 10.1016/j.neucom.2014.05.038
9	Mazrooei-Sebdani R , Farjami S . On a discrete-time-delayed Hopfield neural network with ring structures and different internal decays: Bifurcations analysis and chaotic behavior. Neurocomputing, 2015, 151: 188- 195 doi: 10.1016/j.neucom.2014.06.079
10	Wang Q , Fang Y Y , Li H , Su L J , Dai B X . Anti-periodic solutions for high-order Hopfield neural networks with impulses. Neurocomputing, 2014, 138: 339- 346 doi: 10.1016/j.neucom.2014.01.028
11	Yang L , Li Y K . Existence and exponential stability of periodic solution for stochastic Hopfield neural networks on time scales. Neurocomputing, 2015, 167: 543- 550 doi: 10.1016/j.neucom.2015.04.038
12	Wang C . Piecewise pseudo-almost periodic solution for impulsive non-autonomous high-order Hopfield neural networks with variable delays. Neurocomputing, 2016, 171: 1291- 1301 doi: 10.1016/j.neucom.2015.07.054
13	Kaslik E , Sivasundaram S . Multistability in impulsive hybrid Hopfield neural networks with distributed delays. Nonlinear Anal-Real, 2011, 12: 1640- 1649 doi: 10.1016/j.nonrwa.2010.10.018
14	Park M J , Kwon O M , Park J H , Lee S M . Simplified stability criteria for fuzzy Markovian jumping Hopfield neural networks of neutral type with interval time-varying delays. Expert Syst Appl, 2012, 39: 5625- 5633 doi: 10.1016/j.eswa.2011.11.055
15	Wang H , Yu Y G , Wen G G . Stability analysis of fractional-order Hopfield neural networks with time delays. Neural Netw, 2014, 55: 98- 109 doi: 10.1016/j.neunet.2014.03.012
16	Wang H , Yu Y G , Wen G G , et al. Global stability analysis of fractional-order Hopfield neural networks with time delay. Neurocomputing, 2015, 154: 15- 23 doi: 10.1016/j.neucom.2014.12.031
17	Dharani S , Rakkiyappan R , Cao J D . New delay-dependent stability criteria for switched Hopfield neural networks of neutral type with additive time-varying delay components. Neurocomputing, 2015, 151: 827- 834 doi: 10.1016/j.neucom.2014.10.014
18	Song B , Zhang Y , Shu Z , Hu F N . Stability analysis of Hopfield neural networks perturbed by Poisson noises. Neurocomputing, 2016, 196: 53- 58 doi: 10.1016/j.neucom.2016.02.034
19	Zhang S , Yu Y G , Wang Q . Stability analysis of fractional-order Hopfield neural networks with discontinuous activation functions. Neurocomputing, 2016, 171: 1075- 1084 doi: 10.1016/j.neucom.2015.07.077
20	Liao X X , Luo Q , Zeng Z G . Positive invariant and global exponential attractive sets of neural networks with time-varying delays. Neurovomputing, 2008, 71: 513- 518 doi: 10.1016/j.neucom.2007.07.017
21	Crauel H , Debussche A , Flandoli F . Random attractors. J Dynam Differ Equ, 1995, 9: 307- 341
22	Kloeden P , Stonier D J . Cocycle attractors in nonautonomously perturbed dif- ferential equations. Dynam Continuous Discrete Impulsive Systems, 1998, 4: 211- 226
23	Cheban D N . Dissipative functional differential equations. Bull Acad Sci Rep Moldova Mat, 1991, 2 (5): 3- 12
24	Caraballo T , Marn-Rubio P , Valero J . Autonomous and non-autonomous attractors for differential equations with delays. J Differ Equ, 2005, 208: 9- 41 doi: 10.1016/j.jde.2003.09.008
25	Caraballo T , Kloeden P E , Real J . Pullback and forward attractors for a damped wave equation with delays. Stoch Dyn, 2004, 4: 405- 423 doi: 10.1142/S0219493704001139
26	Caraballo T , Real J . Attractors for 2D-Navier-Stokes models with delays. J Differ Equ, 2004, 205: 271- 297 doi: 10.1016/j.jde.2004.04.012
27	Zhang L X , Boukas E K , Haidar A . Delay-range-dependent control synthesis for time-delay systems with actuator saturation. Automatica, 2008, 44: 2691- 2695 doi: 10.1016/j.automatica.2008.03.009
28	Xu D Y . Integro-differential equations and delay integral inequalities. Tohoku Math J, 1992, 44: 365- 378 doi: 10.2748/tmj/1178227303
29	Zhao H Y . Invariant set and attractor of nonautonomous functional differential systems. J Math Anal Appl, 2003, 282: 437- 443 doi: 10.1016/S0022-247X(02)00370-0
30	Xu D Y , Yang Z C . Attracting and invariant sets for a class of implusive functional defferential equations. J Math Anal Appl, 2007, 329: 1036- 1044 doi: 10.1016/j.jmaa.2006.05.072
31	Tian H . The exponential asymtotic stability of singularly perturbed delay differential equations with a bounded lag. J Math Anal Appl, 2002, 270: 143- 149 doi: 10.1016/S0022-247X(02)00056-2
32	Xu D Y , Yang Z G . Exponential stability of nonlinear implusive neutral differential equations with delays. Nonlinear Anal Theory Methods Appl, 2007, 67: 1426- 1439 doi: 10.1016/j.na.2006.07.043
33	Zhu W . Global exponential stability of impulisive reaction-diffusion equation with variable delays. Appl Math Comput, 2008, 205: 362- 369
34	Teng L Y , Xu D Y . Global attracting set for non-autonomous neutral networks with distributed delays. Neurocomputing, 2012, 94: 64- 67 doi: 10.1016/j.neucom.2012.04.020
35	Liu L , Zhu Q X , Feng L C . Lagrange stability for delayed recurrent neural networks with Markovian switching based on stochastic vector Halandy inequalities. Neurocomputing, 2018, 275: 1614- 1621 doi: 10.1016/j.neucom.2017.10.006
36	Popa A C . Global exponential stability of neutral-type octonion-valued neural networks with time-varying delays. Neurocomputing, 2018, 309: 117- 133 doi: 10.1016/j.neucom.2018.05.004
37	LaSalle J P. The Stability of Dynamical System. Philadelphia: SIAM, 1976

Metrics

Viewed

Full text

121

HTML			PDF

Just accepted	Online first	Issue	Just accepted	Online first	Issue
0	0	1	0	0	120

From	Others	local

Times	2	119
Rate	2%	98%

Abstract

Just accepted	Online first	Issue

0	0	75

From	Others	local

Times	74	1
Rate	99%	1%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed

[1]	杨甲山, 李同兴. 时间模上一类二阶阻尼Emden-Fowler型动态方程的振荡性[J]. 数学物理学报, 2018, 38(1): 134-155.
[2]	黄祖达. 一类具反馈控制的时滞飞蝇方程的伪概周期解[J]. 数学物理学报, 2016, 36(3): 558-568.
[3]	罗日才, 许弘雷, 王五生. 一类新的变时滞中立型神经网络的全局渐近稳定性条件[J]. 数学物理学报, 2015, 35(3): 634-640.
[4]	阿卜杜杰力力·阿卜杜热合曼, 蒋海军, 滕志东. 具有混合变时滞的脉冲Cohen-Grossberg神经网络的指数同步[J]. 数学物理学报, 2015, 35(3): 545-557.
[5]	席博彦, 祁锋. s-对数凸函数的Hermite-Hadamard型积分不等式[J]. 数学物理学报, 2015, 35(3): 515-524.
[6]	吴宇, 唐敏, 周察金. 一类非线性弱奇性Wendroff型积分不等式[J]. 数学物理学报, 2014, 34(6): 1465-1473.
[7]	刘琼. 一个具多参数核为双曲余切函数的积分不等式[J]. 数学物理学报, 2014, 34(4): 851-858.
[8]	刘琼, 龙顺潮. 一个推广的Hilbert型积分不等式[J]. 数学物理学报, 2014, 34(1): 179-185.
[9]	张雨田, 罗琦. 具反应扩散项和Neumann边界条件的脉冲变时滞细胞神经网络的全局指数稳定性[J]. 数学物理学报, 2013, 33(4): 777-786.
[10]	匡继昌. 赋范线性空间中的Hilbert型积分不等式[J]. 数学物理学报, 2013, 33(1): 1-5.
[11]	洪勇. 一类具有最佳常数因子的Hardy 型多重积分不等式[J]. 数学物理学报, 2011, 31(6): 1586-1591.
[12]	李俊民. 非线性参数化时变时滞系统自适应迭代学习控制[J]. 数学物理学报, 2011, 31(3): 682-690.
[13]	辛冬梅, 杨必成. 一个新的Hilbert型积分不等式的推广[J]. 数学物理学报, 2010, 30(6): 1648-1653.
[14]	罗日才, 王五生, 许弘雷. 一类非连续函数积分不等式中未知函数的估计及其应用[J]. 数学物理学报, 2010, 30(4): 1176-1182.
[15]	鲁圣洁, 陶祥兴. 多重的非对称核Hardy-Hilbert积分不等式[J]. 数学物理学报, 2009, 29(3): 597-606.