中立型延迟微分系统常出现在生态学、物理学、自动控制等科学与工程领域中^{[1, 7]},其特征是系统右端函数不仅依赖于过去时间的状态,而且还依赖于过去时间状态的变化率.只有极少数中立型延迟微分方程能够获得解析解表达式,其数值分析文献主要研究了线性问题^{[1, 3, 6]}和一些非线性问题^{[1, 10-12]}的稳定性以及基于Lipschitz条件的非线性问题数值解的收敛性.

目前,仅有少量文献研究方程解的渐近估计.鉴于渐近估计不仅比渐近稳定性描述解的性态更加精确,而且能给出非稳定情形解的上界估计式. Iserles在文献[6]中构造了自治中立型比例延迟微分系统Dirichlet级数形式的解,获得了解析解的上界估计式及渐近稳定的充分条件. Liu等^[8-9]考虑了非自治中立型比例延迟微分系统,获得了解析解的渐近估计. Čermák等^[2]考虑了用梯形方法求解非自治非中立型变延迟微分方程,借助于一个泛函不等式获得了数值解的上界估计式及其渐近稳定的一个充分条件. Zhang等^[13]考虑了用$ \theta $ -方法求解非自治中立型比例延迟微分方程,获得了数值解的上界估计式及其渐近稳定的一个充分条件.

本文在文献[2, 13]的基础上,研究非自治变延迟中立型微分方程梯形方法的渐近估计,获得了数值解的上界估计式及其渐近稳定的一个充分条件,并用数值算例验证了所获结果.因为变延迟中立型微分方程更一般化且更难分析处理,故这样的推广是很有必要的.

考虑一类变延迟中立型微分方程

(2.1) $ \begin{equation} y'(t ) = a(t)y(t)+b(t)y(\theta(t))+ c(t)y^\prime(\phi(t)), \ t\geq t_0, \end{equation} $

其中$ a(t), b(t), c(t) $是区间$ [t_0, \infty) $上的非零复值连续函数, $ \theta(t), \phi(t) $是两个可微函数且严格单调递增,进一步, $ \theta(t_0) = t_0, \phi(t_0) = t_0 $,对任意的$ t > t_0 $满足$ \theta(t) < t, \phi(t) < t $.记$ \psi(t) = \theta^{-1}(t) $, $ \xi(t) = \phi^{-1}(t) $.对方程(2.1)两边同时积分得

(2.2) $ \begin{equation} y(t_{n+1}) -y(t_{n}) = \int\nolimits_{t_{n}}^{t_{n+1}} a(s)y(s){\rm d}s + \int\nolimits_{t_{n}}^{t_{n+1}} b(s)y(\theta(s)){\rm d}s + \int\nolimits_{t_{n}}^{t_{n+1}} c(s)y^\prime(\phi(s)){\rm d}s, \end{equation} $

其中$ t_n = t_0 + nh $，$ h > 0 $为给定步长.记$ u_n : = u(t_n) $$ (u = y, a, b, c, \theta, \phi) $, $ \overline{ v}_n : = (v_n - t_0)/h $$ (v = \theta, \phi) $, $ w(x) = c'(\xi(x)) (\xi'(x))^2 + c(\xi(x)) \xi''(x) $,以及$ w_{\phi_{n }} : = w(\phi_{n }) $.用梯形方法对(2.2)式右端积分进行离散得

(2.3) $ \begin{eqnarray} \int\nolimits_{t_{n}}^{t_{n+1}} a(s)y(s){\rm d}s &\approx &\frac{1}{2} h (a_ny_n +a_{n+1}y_{n+1}), \\ \int\nolimits_{t_{n}}^{t_{n+1}} b(s)y(\theta(s)){\rm d}s & = &\int\nolimits_{\theta_n}^{\theta_{n+1}} b(\psi(x)) y(x) \psi'(x){\rm d}x \\ & = &\frac{1}{2} (\theta_{n+1}-\theta_n ) ( b_n y^h(\theta_n) \psi'(\theta_n) + b_{n+1} y^h(\theta_{n+1}) \psi'(\theta_{n+1})) \\ &\approx &h b_n ( \beta_n y_{[\overline{ \theta }_n]} +\alpha_n y_{[\overline{ \theta }_n]+1} ) , \\ \int\nolimits_{t_{n}}^{t_{n+1}} c(s)y'(\phi(s)){\rm d}s & = & c(\xi(x))y(x)\xi'(x)|_{\phi_n}^{\phi_{n+1}} -\int\nolimits_{\phi_n}^{\phi_{n+1}} w(x) y(x) {\rm d}x \\ & = &c_{n+1}y^h(\phi_{n+1})\xi'(\phi_{n+1}) - c_n y^h(\phi_n)\xi'(\phi_n)\\ && -\frac{1}{2} (\phi_{n+1} - \phi_n) ( w_{\phi_{n+1 }} y^h(\phi_{n+1}) + w_{\phi_{n }} y^h(\phi_n) ) \\ &\approx & c_n ( \hat{\alpha_n} y_{[\overline{ \phi }_n]+1} + \hat{\beta_n} y_{[\overline{ \phi }_n]}), \end{eqnarray} $

其中, $ [\cdot] $为取整函数, $ y^h(v_{n+1}) $, $ y^h(v_n) $是$ y_{[\overline{v}_n]} $和$ y_{[\overline{v}_n]+1} $$ (v = \theta, \phi) $的线性组合,即

$ y^h(v_n) \approx (\overline{ v }_n-[\overline{ v}_n]) y_{[\overline{v }_n]+1} +([\overline{v }_n]+1-\overline{ v }_n) y_{[\overline{ v }_n]}, $

$ y^h(v_{n+1}) \approx (\overline{ v }_{n+1}-[\overline{ v }_n]) y_{[\overline{v }_n]+1} +([\overline{ v }_n]+1-\overline{ v }_{n+1}) y_{[\overline{ v }_n]} , $

且

$ \begin{eqnarray*} \alpha_n & = & \frac{1}{2h} (\theta_{n+1}-\theta_n ) \left(\psi'(\theta_n) ( \overline{ \theta }_n - [\overline{ \theta }_n] ) + \frac{b_{n+1}}{b_n} \psi'(\theta_{n+1}) ( \overline{ \theta }_{n+1} - [\overline{ \theta }_n]) \right), \\ \beta_n & = & \frac{1}{2h} (\theta_{n+1}-\theta_n ) \left( \psi'(\theta_n) + \frac{b_{n+1}}{b_n} \psi'(\theta_{n+1}) \right) - \alpha_n , \\ \hat{\alpha_n} & = &\frac{1}{c_n} \left( c_{n+1}\xi'(\phi_{n+1}) - \frac{1}{2} (\phi_{n+1} - \phi_n ) w_{\phi_{n+1 }} \right) ( \overline{ \phi }_{n+1} - [\overline{ \phi }_n]) \\ &&- \frac{1}{c_n} \left( c_n \xi'(\phi_n) + \frac{1}{2} (\phi_{n+1} - \phi_n ) w_{\phi_{n }} \right) ( \overline{ \phi }_n - [\overline{ \phi }_n]), \\ \hat{\beta_n} & = &\frac{1}{c_n} \left( c_{n+1}\xi'(\phi_{n+1}) - \frac{1}{2} (\phi_{n+1} - \phi_n ) w_{\phi_{n+1 }} \right) ( [\overline{ \phi }_n]+1 - \overline{ \phi }_{n+1}) \\ &&- \frac{1}{c_n} \left( c_n \xi'(\phi_n) + \frac{1}{2} (\phi_{n+1} - \phi_n ) w_{\phi_{n }} \right) ([\overline{ \phi }_n] +1 - \overline{ \phi }_n ). \end{eqnarray*} $

综上所述,由方程(2.2)和(2.3)得到如下递推关系

(2.4) $ \begin{equation} y_{n+1} = R_n y_n + h S_n(\beta _n y_{[\overline{ \theta }_n]} + \alpha_n y_{[\overline{ \theta }_n]+1}) + T_n (\hat{\beta_n} y_{[\overline{ \phi }_n]} + \hat{\alpha_n} y_{[\overline{ \phi }_n]+1}) , \end{equation} $

其中

(2.5) $ \begin{equation} R_n = \frac{2+h a_n}{2-h a_{n+1}}, \quad S_n = \frac{2b_n}{2-h a_{n+1}}, \quad T_n = \frac{2c_n }{2-h a_{n+1}} . \end{equation} $

本节将构造方程(2.4)的解$ y_n $的渐近估计.考虑不等式

(3.1) $ \begin{equation} |S_n |h (|\beta_n| \varrho_{[\overline{ \theta }_n]} + |\alpha_n | \varrho_{[\overline{ \theta }_n]+1}) + | T_n | (|\hat{\beta_n}| \varrho_{[\overline{ \phi }_n]} + |\hat{\alpha_n}| \varrho_{[\overline{ \phi }_n]+1}) \leq (1-|R_n|)\varrho_n, \end{equation} $

并假设

(3.2) $ \begin{equation} \begin{array}{lll} \tilde{S}: = \sup\limits_{n\in Z^+}(\left| S_n\right|) < \infty, \; \; \tilde{R}: = \sup\limits_{n\in Z^+}{\left| R_n\right|}< 1, \; \; \tilde{T}: = \sup\limits_{n\in Z^+}(\left| T_n\right|) < \infty, \\ \eta: = \sup\limits_{n\in Z^+}(| \alpha_n|+| \beta_n|) <\infty, \quad \tilde{\eta}: = \sup\limits_{n\in Z^+}(| \hat{\alpha_n}|+|\hat{\beta_n} |)<\infty , \end{array} \end{equation} $

及

(3.3) $ \begin{equation} \tilde{\gamma}: = \frac{h\tilde{S}\eta +\tilde{T} \tilde{\eta}}{1-\tilde{R}}. \end{equation} $

不等式(3.1)在本文中起着极其重要的作用,只须找到(3.1)式的一个显式解,即可构造出方程(2.4)解$ y_n $的渐近估计.为此考虑辅助方程(参见文献[2, 4])

(3.4) $ \begin{equation} \varphi(\tau(t)) = \nu \varphi(t), \quad \nu = \tau'(t_0), \ t\geq t_0. \end{equation} $

在区间$ [t_0, \infty) $上,当$ \tau(t) \in C^2([t_0, \infty)) $, $ \tau(t_0) = t_0 $, $ \tau(t) < t $时, $ \tau'(t) > 0 $且$ \tau'(t_0) < 1 $,则方程(3.4)的解$ \varphi $存在唯一、连续可微、严格递增并满足$ \varphi'(t_0) = 1 $,且

(3.5) $ \begin{equation} \varphi(t) = \lim\limits_{n\rightarrow \infty } \nu^{-n} ( \tau^n(t)- t_0 ), \quad \nu = \tau'(t_0), \ t\geq t_0, \end{equation} $

其中$ \tau^n(t) $是$ \tau(t) $的第$ n $步迭代.利用这些性质可以得到下述引理.

引理3.1^[2]  设$ \tau(t) \in C^2([t_0, \infty)) $,对任意$ t > t_0 $, $ \tau(t_0) = t_0 $, $ \tau(t) < t $, $ \tau'(t) > 0 $以及$ \tau'(t) $在$ [t_0, \infty) $上递减且$ \tau'(t_0) < 1 $,则由(3.5)式定义的函数$ \varphi(t) $是方程(3.4)的解, $ \varphi'(t) $非负连续且在区间$ [t_0, \infty) $上单调递减,并满足$ \frac{\varphi'(t)}{\varphi(t)} \leq \frac{1}{t-t_0}. $

定义

(3.6) $ \begin{equation} \tau(t) = \left\{ \begin{array}{ll} \max(\theta(t), \phi(t)), \quad &{\hbox{当}}\; \; \tilde{\gamma} \geq 1 , \\ \min (\theta(t), \phi(t)), &{\hbox{当}}\; \; 0< \tilde{\gamma}< 1, \end{array}\right. \end{equation} $

显然, $ \tau(t) $满足引理3.1中的所有假设条件.

定理3.1 假设(3.2)式成立, $ \tilde{\gamma} $和$ \varphi(t) $分别由(3.3)与(3.5)式给定, $ t^\star \geq t_0 $是方程$ t- \tau(t) = h $的唯一实根且$ k^\star = [(t^\star -t_0)/h] +1, $则序列

(3.7) $ \begin{equation} \varrho_n = \left\{ \begin{array}{ll} (\varphi(t_0 +(n-k^\star )h) )^{-\log_{\nu} \tilde{\gamma}}, \quad &{\hbox{当}} \; \; \tilde{\gamma} \geq1, \\ (\varphi(t_0 +(n+k^\star )h) )^{-\log_{\nu} \tilde{\gamma}}, &{\hbox{当}} \; \; 0< \tilde{\gamma}< 1, \end{array} \right. \end{equation} $

定义了方程(3.1)的一个正解,即$ \varrho_n > 0 $且满足方程(3.1).

证 令$ \overline{ \tau }_n = (\tau_n- t_0)/h $.当$ \tilde{\gamma}\geq 1 $时, $ \varrho_n $是一个递增序列,则利用(3.4), (3.6)和(3.7)式得

$ \begin{eqnarray*} &&| S_n |h (|\beta _n| \varrho_{[\overline{ \theta }_n]} + |\alpha_n | \varrho_{[\overline{ \theta }_n]+1}) + |T_n| \big(|\hat{\beta_n}| \varrho_{[\overline{ \phi }_n]} + |\hat{\alpha_n}| \varrho_{[\overline{ \phi }_n]+1}\big) \\ & \leq& ( |S_n|h (|\beta _n| + |\alpha_n | ) + |T_n| (|\hat{\beta_n}| + |\hat{\alpha_n}| ))\varrho_{[\overline{ \tau }_n]+1} \\ & \leq&(h\tilde{S}\eta+\tilde{T}\tilde{\eta}) \left(\varphi(t_0 +\overline{ \tau }_n h+h-k^\star h)\right)^{-\log_{\nu}\tilde{\gamma}} \\ &\leq& (h\tilde{S}\eta+\tilde{T}\tilde{\eta}) \left(\varphi( \tau_{(n-k^\star) h})\right)^{-\log_{\nu}\tilde{\gamma}} \\ & = &(1- \tilde{ R}) \varrho_n, \end{eqnarray*} $

即对所有的$ n \geq k^\star $,当$ \tilde{\gamma}\geq 1 $时,不等式(3.1)成立.类似可证得当$ 0 < \tilde{\gamma} < 1 $时,对所有的$ n\in N^+ $,不等式(3.1)成立.

至此,我们显式给出了不等式(3.1)的一个解序列,进而能得到方程(2.4)解$ y_n $的渐近估计.

定理3.2 设$ y_n $是方程(2.4)的一个解,如果(3.2)式成立, $ \tilde{\gamma} $和$ \varphi(t) $分别由(3.3)与(3.5)式给定且$ \nu = \tau'(t_0) $,则

(3.8) $ \begin{equation} y_n = O\left((\varphi(n))^{-\log_{\nu}\tilde{\gamma}}\right), \quad {\hbox{当}}\ n\rightarrow \infty . \end{equation} $

特别地,当$ 0 < \tilde{\gamma} < 1 $时,其解渐近稳定.

证 首先,对方程(2.4)作变换$ z_n = y_n/\varrho_n $, $ \varrho_n $由(3.7)式给定,则

(3.9) $ \begin{eqnarray} z_{n+1}\varrho_{n+1} & = & R_n z_n \varrho_n + h S_n(\beta _n z_{[\overline{ \theta }_n]}\varrho_{[\overline{ \theta }_n]} + \alpha_n z_{[\overline{ \theta }_n]+1}\varrho_{[\overline{ \theta }_n]+1}) \\ &&+ T_n (\hat{\beta_n} z_{[\overline{ \phi }_n]}\varrho_{[\overline{ \phi }_n]} + \hat{\alpha_n} z_{[\overline{ \phi }_n]+1}\varrho_{[\overline{ \phi }_n]+1}). \end{eqnarray} $

当$ n\rightarrow \infty $时,我们需要证明方程(3.9)的任意解$ z_n $均有界.取$ \sigma_0 > \max \left\{\frac{1+\nu }{1-\nu }, \frac{ \tau^{-1}(t_0+k^\star h)- t_0 }{h}\right\} $, $ \sigma_0 \in Z^+ $且定义区间$ I_0: = [[\overline{ \tau }_{\sigma_0}] $, $ \sigma_0]\cap Z^+ $,及$ \sigma_{m+1} : = [\frac{ \tau^{-1}(t_0+(\sigma_m -1)h)-t_0 }{h}] $,这里$ m = 0, 1, \cdots $, $ I_{m+1}: = [\sigma_m, \sigma_{m+1}]\cap Z^+ $,记

$ B_m : = \sup\Big( |z_k |, k \in \bigcup\limits_{j = 0}^m I_j\Big), \quad m = 0, 1, 2, \cdots . $

考虑任意的$ n^\star \in I_{m+1} $, $ n^\star > \sigma _m $,我们希望通过$ z_k $来估计$ z_{n^\star} $,其中$ k \in \bigcup\limits_{j = 0}^m I_j $,分三种情况进行讨论:

(ⅰ)假设$ R_{n^{\star}-1} = 0 $,则

$ \begin{eqnarray*} z_{n^\star} & = & \frac{1}{\varrho_{n^\star}} \left( S_{{n^\star-1}} h (\beta _{n^{\star}-1} z_{[\overline{ \theta }_{n^{\star}-1}]} \varrho_{[\overline{ \theta }_{n^{\star}-1}]} + \alpha_{n^{\star}-1} z_{[\overline{ \theta }_{n^{\star}-1}]+1} \varrho_{[\overline{ \theta }_{n^{\star}-1}]+1}) \right. \\ &&\left. + T_{n^{\star}-1} (\hat{\beta}_{n^{\star}-1} z_{[\overline{ \phi }_{n^{\star}-1}]}\varrho_{[\overline{ \phi }_{n^{\star}-1}]} + \hat{\alpha}_{n^{\star}-1} z_{[\overline{ \phi }_{n^{\star}-1}]+1} \varrho_{[\overline{ \phi }_{n^{\star}-1}]+1}) \right). \end{eqnarray*} $

对上式两边取绝对值且由不等式(3.1)估计$ |z_{n^\star} | $得

$ \begin{eqnarray*} |z_{n^\star} | &\leq& B_m \frac{1}{\varrho_{n^\star}} | S_{{n^\star-1}} h (\beta _{n^{\star}-1} \varrho_{[\overline{ \theta }_{n^{\star}-1}]} + \alpha_{n^{\star}-1} \varrho_{[\overline{ \theta }_{n^{\star}-1}]+1}) \\ &&+ T_{n^{\star}-1} (\hat{\beta}_{n^{\star}-1} \varrho_{[\overline{ \phi }_{n^{\star}-1}]} + \hat{\alpha}_{n^{\star}-1} \varrho_{[\overline{ \phi }_{n^{\star}-1}]+1})| \\ & \leq & B_m \frac{1}{\varrho_{n^\star}}(1-R_{n^\star-1}) \varrho_{n^\star-1} \leq B_m \frac{\varrho_{n^\star-1}}{\varrho_{n^\star}}. \end{eqnarray*} $

当$ \tilde{\gamma} \geq 1 $时, $ \varrho_n $是一个递增序列,故$ \left|z_{n^\star}\right| \leq B_m \frac{\varrho_{n^\star-1}}{\varrho_{n^\star}} \leq B_m $.当$ 0 < \tilde{\gamma} < 1 $时, $ \varrho_n $是一个递减序列,利用中值定理,二项式定理及定理3.2,得

$ \begin{eqnarray*} |z_{n^\star}| &\leq& B_m \frac{\varrho_{n^\star-1}}{\varrho_{n^\star}} = B_m \Big(\frac{\varphi(t_0 +(n^\star+k^\star )h)} {\varphi(t_0 +(n^\star-1+k^\star )h)}\Big)^{\log_{\nu}\tilde{\gamma}} \\ & \leq& B_m \Big(1+h \frac{\varphi'(t_0 +(n^\star-1+k^\star )h)} {\varphi(t_0 +(n^\star-1+k^\star )h)}\Big)^{\log_{\nu}\tilde{\gamma}} \\ & \leq& B_m\Big (1+h \frac{1} {(n^\star-1+k^\star )h}\Big)^{\log_{\nu}\tilde{\gamma}} \\ & \leq& B_m \Big(1+ \frac{K_1} {\sigma_m}\Big), \end{eqnarray*} $

其中$ K_1 > 0 $为正常数.

(ⅱ)假设对任意的$ n \in [\sigma_m, n^\star-1] \cap Z^+ $满足$ R_n \neq 0 $,则(3.9)式两边同乘$ \prod\limits_{l = \sigma_m}^{n}\frac{1}{R_l} $得

$ \begin{eqnarray*} \triangle (z_n\varrho_n \prod\limits_{l = \sigma_m}^{n-1}\frac{1}{R_l}) & = & \left( h S_n(\beta _n z_{[\overline{ \theta }_n]}\varrho_{[\overline{ \theta }_n]} + \alpha_n z_{[\overline{ \theta }_n]+1}\varrho_{[\overline{ \theta }_n]+1}) \right.\\ &&\left. + T_n (\hat{\beta_n} z_{[\overline{ \phi }_n]}\varrho_{[\overline{ \phi }_n]} + \hat{\alpha_n} z_{[\overline{ \phi }_n]+1}\varrho_{[\overline{ \phi }_n]+1}) \right) \prod\limits_{l = \sigma_m}^{n}\frac{1}{R_l} , \end{eqnarray*} $

其中$ \triangle $是向前差分.两边从$ \sigma_m $到$ n^\star-1 $求和得

$ \begin{eqnarray*} z_{n^{\star}} & = & z_{\sigma_m}\frac{\varrho_{\sigma_m}}{\varrho_{n^{\star}}} \prod\limits_{l = \sigma_m}^{n^\star-1}R_l + \frac{1}{\varrho_{n^{\star}}} \sum\limits_{i = \sigma_m}^{n^{\star}-1} \left( h S_i(\beta _i z_{[\overline{ \theta }_i]}\varrho_{[\overline{ \theta }_i]} + \alpha_i z_{[\overline{ \theta }_i]+1}\varrho_{[\overline{ \theta }_i]+1}) \right. \\ &&\left. + T_i (\hat{\beta_i} z_{[\overline{ \phi }_i]}\varrho_{[\overline{ \phi }_i]} + \hat{\alpha_i} z_{[\overline{ \phi }_i]+1}\varrho_{[\overline{ \phi }_i]+1}) \right) \prod\limits_{l = i+1}^{n^{\star}-1}{R_l}. \end{eqnarray*} $

对上式两边取绝对值得

(15) $ \begin{equation} \left|z_{n^{\star}} \right|\leq B_m \left( \frac{\varrho_{\sigma_m}}{\varrho_{n^{\star}}} \prod\limits_{l = \sigma_m}^{n^{\star}-1}{\left| R_l \right|} + \frac{1}{\varrho_{n^{\star}}} \sum\limits_{i = \sigma_m}^{n^{\star}-1}(1-| R_i|)\varrho_i \prod\limits_{l = i+1}^{n^{\star}-1}{| R_l |} \right). \end{equation} $

又因为

$ (1-\left| R_i \right|)\prod\limits_{l = i+1}^{n^{\star}-1}| R_l | = \prod\limits_{l = i+1}^{n^{\star}-1}| R_l | - \prod\limits_{l = i}^{n^{\star}-1}| R_l | = \triangle \prod\limits_{l = i}^{n^{\star}-1}| R_l |, $

所以把上式代入(3.10)式且部分求和得

$ \begin{eqnarray*} |z_{n^{\star}} | & \leq& B_m \left( \frac{\varrho_{\sigma_m}}{\varrho_{n^{\star}}} \prod\limits_{l = \sigma_m}^{n^{\star}-1}{| R_l |} + \frac{1}{\varrho_{n^{\star}}} \sum\limits_{i = \sigma_m}^{n^{\star}-1}\varrho_i \triangle \prod\limits_{l = i}^{n^{\star}-1}{| R_l |} \right) \\ & = & B_m \left( \frac{\varrho_{\sigma_m}}{\varrho_{n^{\star}}} \prod\limits_{l = \sigma_m}^{n^{\star}-1}{| R_l |} +1- \prod\limits_{l = \sigma_m}^{n^{\star}-1}{| R_l |} \frac{\varrho_{\sigma_m}}{\varrho_{n^{\star}}} -\sum\limits_{i = \sigma_m}^{n^{\star}-1} \prod\limits_{l = i+1}^{n^{\star}-1}{| R_l |} \frac{\triangle \varrho_i }{\varrho_{n^{\star}}} \right) \\ & = &B_m \left( 1- \frac{1}{\varrho_{n^{\star}}} \sum\limits_{i = \sigma_m}^{n^{\star}-1}{\triangle \varrho_i } \prod\limits_{l = i+1}^{n^{\star}-1}{| R_l |} \right) \\ & = &B_m \left( 1- \frac{1}{\varrho_{n^{\star}}} \sum\limits_{i = \sigma_m}^{n^{\star}-1} {\frac{\triangle \varrho_i }{1-| R_i |}} \triangle \prod\limits_{l = i}^{n^{\star}-1}{| R_l |} \right). \end{eqnarray*} $

当$ \tilde{\gamma} \geq 1 $时, $ \varrho_n $是一个递增序列且$ \triangle \varrho_i\geq 0 $,故$ \left|z_{n^{\star}} \right|\leq B_m $.当$ 0 < \tilde{\gamma} < 1 $时, $ \varrho_n $是一个递减序列且$ \triangle \varrho_i\leq 0 $, $ \triangle \varrho_i\geq \triangle \varrho_{i-1} $,利用中值定理及$ \varphi'(t) $单调递减性得

$ \begin{eqnarray*} -\triangle \varrho_{\sigma_m} & = & (\varphi(t_0 +(\sigma_m +k^\star )h))^{-\log_{\nu}\tilde{\gamma}} - (\varphi(t_0 +(\sigma_{m} +1 +k^\star )h))^{-\log_{\nu}\tilde{\gamma}} \\ & \leq &h \log_{\nu}\tilde{\gamma} (\varphi(t_0 +(\sigma_m +k^\star )h))^{-\log_{\nu}\tilde{\gamma}-1} \varphi'(t_0 +(\sigma_m +k^\star )h), \\ \varrho_{\sigma_{m+1}} & = &(\varphi(t_0 +(\sigma_{m+1} +k^\star )h))^{-\log_{\nu}\tilde{\gamma}} \\ & \geq&(\frac{\overline{K}_2}{\nu})^{-\log_{\nu}\tilde{\gamma}} ( \varphi(t_0 + (\sigma_m + k^\star )))^{-\log_{\nu}\tilde{\gamma}}, \end{eqnarray*} $

其中$ \overline{K}_2 $是一个适当的正实数(由(3.4)式可知),再利用不等式$ \frac{-\triangle \varrho_i}{1-\left|R_i \right|} \leq \frac{-\triangle \varrho_{\sigma_m}}{1- \tilde{R} } $得

$ \begin{eqnarray*} |z_{n^{\star}} | & \leq& B_m \left( 1- \frac{\triangle \varrho_{\sigma_m}}{\varrho_{n^{\star}}(1- \tilde{R} )} \sum\limits_{i = \sigma_m}^{n^{\star}-1} \triangle \prod\limits_{l = i}^{n^{\star}-1}{| R_l |} \right) \\ & = &B_m \left( 1- \frac{\triangle \varrho_{\sigma_m}}{\varrho_{n^{\star}}(1- \tilde{R})} (1-\prod\limits_{i = \sigma_m}^{n^{\star}-1}{| R_l |}) \right) \\ & \leq &B_m \left( 1- \frac{\triangle \varrho_{\sigma_m}}{\varrho_{\sigma_{m+1}}(1- \tilde{R} )} \right) \\ & \leq& B_m \left( 1 + \frac{h \log_{\nu}\tilde{\gamma} \varphi'(t_0 +(\sigma_m +k^\star )h) } {(1- \tilde{R}) (\varphi(t_0 +(\sigma_m +k^\star )h))} (\frac{\overline{K}_2}{\nu})^{-\log_{\nu}\tilde{\gamma}} \right) \\ & \leq & B_m \Big( 1+\frac{K_2}{ \sigma_m }\Big), \end{eqnarray*} $

其中$ K_2 $的一个正常数.

(ⅲ)假设$ R_{n^{\star}-1} \neq 0 $且存在$ k \in [\sigma_m, n^\star-2] \cap Z^+ $使得$ R_k = 0 $.定义$ \sigma^\star : = \sup(k, k \in [\sigma_m, n^{\star}-2] \cap Z^+ $及$ R_n = 0 $),则

$ R_{\sigma^{\star}} = 0, R_{\sigma^{\star}+1} \neq 0, R_{n^{\star}} \neq 0. $

对方程(3.9)两边同乘$ \prod\limits_{l = \sigma^{\star}+1}^{n}\frac{1}{R_l} $,且从$ \sigma^{\star}+1 $到$ n^{\star}-1 $求和得

$ \begin{eqnarray*} z_{n^{\star}} & = &z_{\sigma^\star+1} \frac{\varrho_{\sigma^\star+1}}{\varrho_{n^{\star}}} \prod\limits_{l = \sigma^{\star}+1}^{n^{\star}-1}{R_l} + h \frac{1}{\varrho_{n^{\star}}} \sum\limits_{i = \sigma^\star+1}^{n^{\star}-1} \left( h S_i(\beta _i z_{[\overline{ \theta }_i]}\varrho_{[\overline{ \theta }_i]} + \alpha_i z_{[\overline{ \theta }_i]+1}\varrho_{[\overline{ \theta }_i]+1}) \right. \\ & &\left. + T_i (\hat{\beta_i} z_{[\overline{ \phi }_i]}\varrho_{[\overline{ \phi }_i]} + \hat{\alpha_i} z_{[\overline{ \phi }_i]+1}\varrho_{[\overline{ \phi }_i]+1}) \right) \prod\limits_{l = i+1}^{n^{\star}-1}{R_l}. \end{eqnarray*} $

由$ \sigma^\star $的定义知$ R_{\sigma^\star} = 0 $,则由情况(i)结论得到估计式

$ \left|z_{\sigma^\star+1}\right| \leq B_m \Big (1+ \frac{K_1}{\sigma_m}\Big), \quad K_1 > 0. $

又由(3.1)式得

$ |z_{n^\star}| \leq B_m \Big(1+ \frac{K_1}{\sigma_m}\Big) \left( \frac{\varrho_{\sigma^\star+1}}{\varrho_{n^{\star}}} \prod\limits_{l = \sigma^\star+1}^{n^{\star}-1}{\left| R_l \right|} + \frac{1}{\varrho_{n^{\star}}} \sum\limits_{i = \sigma^\star+1}^{n^{\star}-1}(1-| R_i |)\varrho_i \prod\limits_{l = i+1}^{n^{\star}-1}{| R_l |} \right), $

上式即为对不等式(3.10)右端作相应修改(用$ \sigma^\star+1 $代替$ \sigma_m $).采用情况(ⅱ)相同技巧,得

$ \left|z_{n^\star}\right| \leq B_m\Big(1+ \frac{K_1}{\sigma_m}\Big) \Big (1+ \frac{K_2}{\sigma_m}\Big) \leq B_m\Big(1+\frac{K_3}{\sigma_m}\Big) , $

其中$ K_3 $是一个正常数.

综上三种情况(ⅰ), (ⅱ), (ⅲ),对任意的$ n^{\star} \in I_{m+1} $, $ n^{\star} > \sigma_m $有

$ \left| z_{n^\star}\right| \leq B_m \left(1+ O(\frac{1}{\sigma_m})\right) , \quad\; m \rightarrow \infty. $

因此$ B_{m+1}\leq B_m (1+ O(1/\sigma_m)) $.当$ m \rightarrow \infty $时,它保证了$ \prod\limits_{j = 1}^m(1+ 1/\sigma_j) $是收敛的.再由引理3.1可得

$ \begin{eqnarray*} \sigma_{m+1} & \geq &\frac{1}{h} ( \theta^{-1}((\sigma_m -1)h +t_0)-t_0 -h ) \\ & \geq& \frac{1}{h} ( \varphi^{-1}(\varphi(\frac{1}{\nu}(\sigma_m -1)h +t_0))-t_0 -h ) \\ & = & \frac{1}{\nu} \sigma_m -\frac{1}{\nu} -1 , \end{eqnarray*} $

故$ \sigma_m \geq \nu^{-m}(\sigma_0- \frac{1+\nu}{1-\nu}) $及相应的无穷积收敛.所以当$ m \rightarrow \infty $时,序列$ {B_m} $一致有界,即(3.8)式成立.

注3.1 当$ \theta(t) = \phi(t) $时, (2.4)式可以改写为

(3.11) $ \begin{equation} y_{n+1} = R_n y_n + (h S_n \beta_n + T_n \hat{\beta_n}) y_{\lfloor\overline{ \theta }_n\rfloor} + (h S_n \alpha_n + T_n \hat{\alpha_n}) y_{\lfloor\overline{ \theta }_n\rfloor+1}), \end{equation} $

考虑不等式

$ |h S_n \beta_n + T_n \hat{\beta_n}| \varrho_{[\overline{ \theta }_n]} + |h S_n \alpha_n + T_n \hat{\alpha_n}| \varrho_{[\overline{ \theta }_n]+1} \leq (1-|R_n|)\varrho_n, $

并假设

(3.12) $ \begin{equation} \begin{array}{lll} \tilde{R}: = \sup\limits_{n\in Z^+}{\left| R_n\right|}< 1, \; \; S_{\alpha}: = \sup\limits_{n\in Z^+}(| h S_n \beta_n + T_n \hat{\beta_n} |) < \infty, \\ S_{\beta}: = \sup\limits_{n\in Z^+}(| h S_n \alpha_n + T_n \hat{\alpha_n}|) < \infty, \end{array} \end{equation} $

及

(3.13) $ \begin{equation} \gamma: = \frac{ S_{\alpha} +S_{\beta}}{1-\tilde{R}}, \end{equation} $

则可以得到方程(3.11)解的渐近估计

(3.14) $ \begin{equation} y_n = O\left((\varphi(n))^{-\log_{\nu}\gamma}\right), \quad {\hbox{当}}\ n\rightarrow \infty . \end{equation} $

特别地,当$ 0 < \gamma < 1 $时,其解渐近稳定.

注3.2 当$ \theta(t) = pt, \phi(t) = \lambda t $均取比例延迟时,辅助方程(3.4)变为

$ \varphi(q t) = q \varphi(t), \quad q = \left\{ \begin{array}{ll} \max(p, \lambda), \quad &{\hbox{当}}\; \; \tilde{\gamma} \geq 1 , \\ \min (p, \lambda), &{\hbox{当}}\; \; 0< \tilde{\gamma}< 1, \end{array}\right. $

引理3.1与定理3.1的所有假设条件显然成立.此时,定理3.2与注3.1均是文献[13]中相关结论的直接推广,所以变延迟项$ \theta(t), \phi(t) $更具一般性.

例3.1 考虑中立型延迟微分方程

$ y'(t ) = a(t)y(t)+b(t)y(t^\varepsilon)+ c(t)y^\prime(t^\varepsilon), \ t\geq 1, $

其中$ 0 < \varepsilon < 1 $, $ a(t), b(t), c(t) $均是区间$ [1, \infty) $上的非零复值连续函数.令$ t_{n } = 1+ nh $, $ \overline{\varepsilon}_n = \frac{ t_n^\varepsilon -1}{h} $, $ w_{\varepsilon_{n }} = c'_n (t_{n }^{1-\varepsilon})^2 + c_n (1-\varepsilon) t_{n }^{1-2\varepsilon} $,则(2.4)式可以改写为

(3.15) $ \begin{equation} y_{n+1} = R_n y_n + (h S_n \beta_n + T_n \hat{\beta_n}) y_{[ \overline{\varepsilon}_n ]} + (h S_n \alpha_n + T_n \hat{\alpha_n}) y_{[ \overline{\varepsilon}_n ]+1}, \end{equation} $

其中$ R_n, S_n, T_n $由(2.5)式给定,且

$ \begin{eqnarray*} \alpha_n & = &\frac{1}{2h\varepsilon } (t_{n+1}^\varepsilon - t_{n }^\varepsilon ) \left( t_{n }^{1-\varepsilon} ( \overline{\varepsilon}_n - [\overline{\varepsilon}_n ] ) +\frac{b_{n+1}}{b_n} t_{n+1}^{1-\varepsilon} ( \overline{\varepsilon}_{n+1} - [ \overline{\varepsilon}_n ] ) \right), \\ \beta_n & = & \frac{1}{2h\varepsilon } (t_{n+1}^\varepsilon - t_{n }^\varepsilon ) \left( t_{n }^{1-\varepsilon} + \frac{b_{n+1}}{b_n} t_{n+1}^{1-\varepsilon} \right) - \alpha_n, \\ \hat{\alpha_n} & = & \frac{1}{c_n \varepsilon} \left( c_{n+1} t_{n+1}^{1-\varepsilon} - \frac{1}{2\varepsilon} ( t_{n+1}^\varepsilon - t_{n }^\varepsilon ) w_{\varepsilon_{n+1 }} \right) ( \overline{\varepsilon}_{n+1} - [\overline{\varepsilon}_n ] ) \\ &&- \frac{1}{c_n \varepsilon} \left( c_n t_{n }^{1-\varepsilon} + \frac{1}{2\varepsilon} (t_{n+1}^\varepsilon-t_{n }^\varepsilon ) w_{\varepsilon_{n }} \right) ( \overline{\varepsilon}_{n } - [\overline{\varepsilon}_n ] ), \\ \hat{\beta_n} & = &\frac{1}{c_n \varepsilon} \left( c_{n+1} t_{n+1}^{1-\varepsilon} - \frac{1}{2\varepsilon} (t_{n+1}^\varepsilon - t_{n }^\varepsilon ) w_{\varepsilon_{n+1 }} \right) (1- \overline{\varepsilon}_{n+1} + [\overline{\varepsilon}_n ] ) \\ && - \frac{1}{c_n \varepsilon} \left( c_n t_{n }^{1-\varepsilon} + \frac{1}{2\varepsilon} (t_{n+1}^\varepsilon-t_{n }^\varepsilon ) w_{\varepsilon_{n }} \right) ( 1-\overline{\varepsilon}_{n } + [\overline{\varepsilon}_n ] ). \end{eqnarray*} $

不难验证,当$ \theta(t) = \phi(t) = t^\varepsilon $时,引理3.1与定理3.2的所有假设条件均成立,其辅助泛函方程(3.4)为

$ \varphi( t^\varepsilon) = \varepsilon \varphi(t), \quad t\geq 1, $

且解$ \varphi(t) = \log t $.借助于上述泛函方程,则可得类似于(3.8)与(3.14)式的渐近估计.

推论3.1 设$ y_n $是方程(3.15)的一个解,如果(3.2)式成立且$ \tilde{\gamma} $是由(3.3)式给定,则

$ y_n = O\left((\log n)^{-\log_{\varepsilon} \tilde{\gamma}}\right), \quad {\hbox{当}}\ n\rightarrow \infty . $

推论3.2  设$ y_n $是方程(3.15)的一个解,如果(3.12)式成立且$ \gamma $是由(3.13)式给定,则

$ y_n = O\left((\log n)^{-\log_{\varepsilon} \gamma}\right), \quad {\hbox{当}}\ n\rightarrow \infty . $

本节将用一个数值例子来验证已获理论结果的正确性及方法的有效性.

例4.1 考虑初值问题

(3.16) $ \begin{equation} y'(t) = -10y(t)- 15y(\frac{t}{2})+ 0.6 y'(\frac{t}{2}), \; \; y(0) = 1, \; \; t \geq 0. \end{equation} $

取步长$ h = 0.05 $,容易计算得$ |R| = 0.6 $, $ |S| = 12 $, $ |T| = 0.48 $, $ \eta = 1 $, $ \tilde{\eta} = 2 $,且$ \tilde{\gamma} = 3.9 $和$ \gamma = 3.15 $.所以本文所得渐近估计(3.8)和(3.14)分别为

(3.17) $ \begin{equation} y_n = O(n^{1.96347412397489}), \qquad {\hbox{当}} \, n \rightarrow \infty, \end{equation} $

(3.18) $ \begin{equation} y_n = O(n^{1.65535182861255}), \qquad {\hbox{当}} \, n \rightarrow \infty, \end{equation} $

即分别存在适当的实常数$ L_1 > 0, L_2 > 0 $使得

$ |y_n | \leq L_1 n^{1.96347412397489}, \qquad n {\hbox{足够大}}, $

$ |y_n | \leq L_2 n^{1.65535182861255}, \qquad n {\hbox{足够大}}. $

因为$ \gamma > 1 $,所以

$ \varrho_n = (n-2)^{1.65535182861255} , \quad |z_n| = |\frac{y_n}{\varrho_n} | = |y_n(n-2)^{-1.65535182861255} |. $

由定理3.2的证明可知,取$ L_2 = B_0 $,且

$ B_0 = \sup(|y_n(n-2)^{-1.65535182861255} |, n\in [[\frac{\sigma_0}{2}], \sigma_0] \cap Z^+). $

令$ \sigma_0 = 20 $,则$ L_2 = B_0 = 0.10490479511068 $,用同样的方法计算得到$ L_1 = 0.05527556369595 $,渐近估计分别为

$ |y_n | \leq 0.05527556369595 \cdot n^{1.96347412397489}, \qquad n \geq 20 , $

$ |y_n | \leq 0.10490479511068 \cdot n^{1.65535182861255}, \qquad n \geq 20 . $

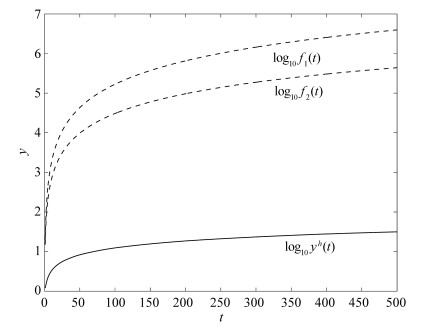
至此,我们给出了方程(3.16)的数值解$ y_{n} $的上界估计式

$ f_1(t) = 0.05527556369595 \left(\frac{t}{h}\right)^{1.96347412397489}, $

$ f_2(t) = 0.10490479511068 \left(\frac{t}{h}\right)^{1.65535182861255}. $

图 1分别给出了$ (t, \log_{10} f_1(t)) $, $ (t, \log_{10} f_2(t)) $和$ (t, \log_{10} y^h(t)) $的图形,其中$ t\in [1, 500] $, $ y^h(t) $是$ y_{n} $和$ y_{n+1} $的线性组合.