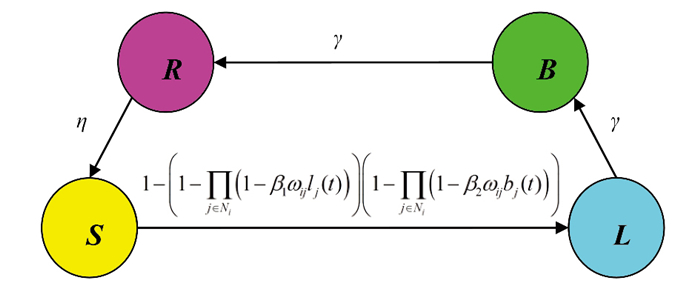1 引言
1987年, Cohen首次提出了第一个计算机病毒传播动力学模型[1].从那时起,许多计算机病毒传播模型相继被提出,例如, SIS模型[2], SIR模型[3-4], SIRS模型[5-7], SEIRS模型[8], SLBS模型[9-13], SIPS模型[14], SIRC模型[15]等.另一方面,网络的拓扑对病毒传播的影响也引起了众多学者的广泛关注,网络上的病毒传播模型被大量提出.例如SI模型[16-17], SIS模型[18-22], SIR模型[23-27]和SLBS模型[28]在网络上被重新提出了.为了研究无向和未加权网络上的病毒传播模型, Wang et al[29], Mieghem[30], Youssef, Scoglio[31]以及Yang[32]等人提出了个体的平均场理论方法(IBMF).然而,由于计算机病毒传播具有方向性,并且接触频率或网络带宽对计算机病毒传播也有影响,那么大多数真实网络可能包含有向边[33]和加权边[34].广义网络可以很好地表示上述真实网络.
为了更好地研究广义网络拓扑对计算机病毒传播的影响,文章受SIR模型启发,将恢复状态(R)引入SLBS模型,提出了一种基于广义网络的新型SLBRS模型.理论结果表明,广义网络的特征值在病毒传播中起着至关重要的作用.
文章的布局如下:在第2节中,详细介绍了广义网络和计算机病毒传播模型.在第3节中,对模型进行了全面分析.在第4节中,得到了数值模拟结果.最后,在第5节中,做出了全文总结.
2 模型
为了详细描述模型,提出以下符号表达式.
在SLBRS模型上,节点可以被分为四组:未感染节点(
令
于是,给出以下假设(参考图 1).
图 1
(H1)易感节点
(H2)潜在节点变成为爆发节点的概率是
(H3)爆发节点变成为恢复节点的概率是
(H4)恢复节点变成为易感节点的概率是
由于
根据(H1)-(H4),可以推导出以下等式
将这些方程代入上述公式并使
在原点附近对非线性模型(2.1)进行线性化,可以得到以三
可以将模型(2.1) (模型(2.2))视为基于广义网络的SLBRS模型.
3 模型分析
非线性系统(2.1)和线性系统(2.2)都具有唯一的无病毒平衡点
令
令
然后,系统(2.2)可以以矩阵的形式表示如下
令
定理 3.1 考虑线性系统(2.2),
(a)如果
(b)如果
证 系统(3.1)在
等式(3.3)有两种可能的情况.
情况 1
该等式具有一个
情况 2
这个等式具有
其中
如果
然后考虑系统(2.2)的全局稳定性.
引理 3.1[35] 考虑在紧凑集
引理 3.2 集合
证
具有
作为法外向量.对于
证毕.
因此,结果遵循引理3.1.
定理 3.3[35] 考虑一个
其中
(C1)对于所有
(C2)对于所有
(C3)原点集是包含集合
(1)
(2)
定理 3.2 考虑线性系统(2.2).如果
证
此外,
线性系统(2.2)是非线性系统(2.1)的上界,即
因此,非线性系统(2.1)中的所有元素都小于线性系统(2.2)中的元素.根据定理3.2,可以得到
定理 3.3 考虑非线性系统(2.1).如果
定理 3.4 考虑线性系统(2.2).如果
这表明如果
定理 3.5 如果
证 注意到系统(2.2)的任何解都是有界的,因此命题的结论很容易从文献[36]的推论(1)得出.
定理 3.6 如果
证 定理3.5可以确定病毒平衡点的存在.需要证明,如果
经过计算,可得出
但对于所有
显然这是矛盾的.
同理,当
现在将证明
其中
如果
可以获得如下等式
根据
如果
或
由于
令
猜想 3.1 考虑系统(2.2),假设
4 数值分析
该节通过一些数值例子来验证上述结论.设
(1)将有250个权重为
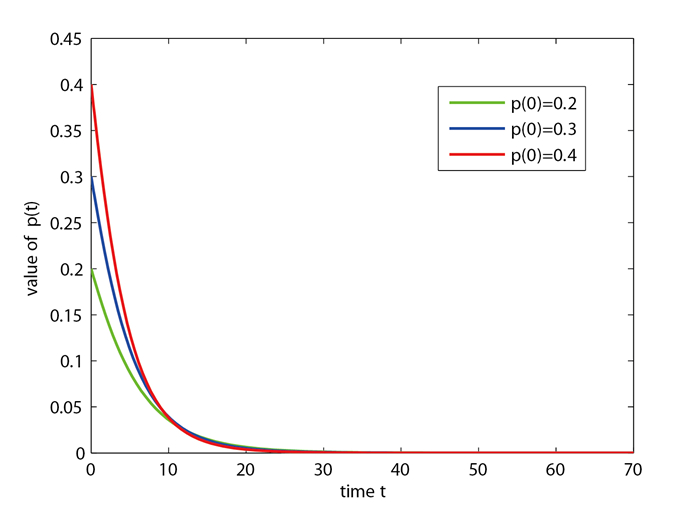
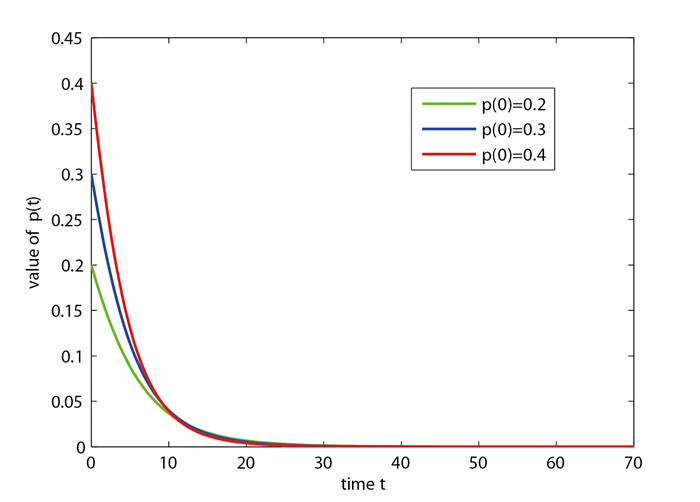
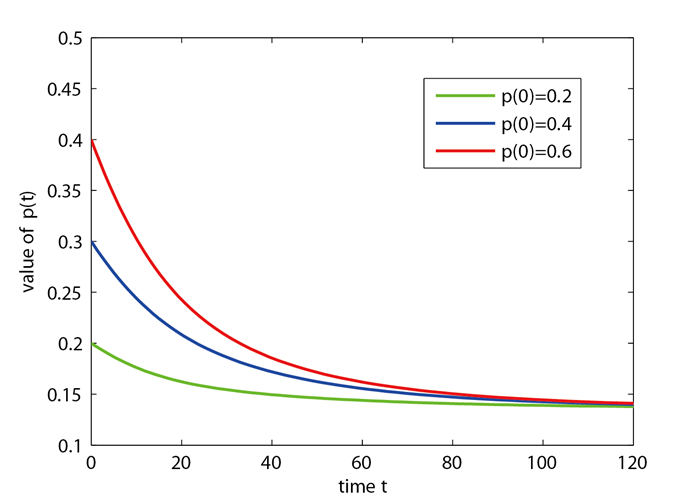
情况 1 非线性系统(2.1)初始条件参数取值为
图 2
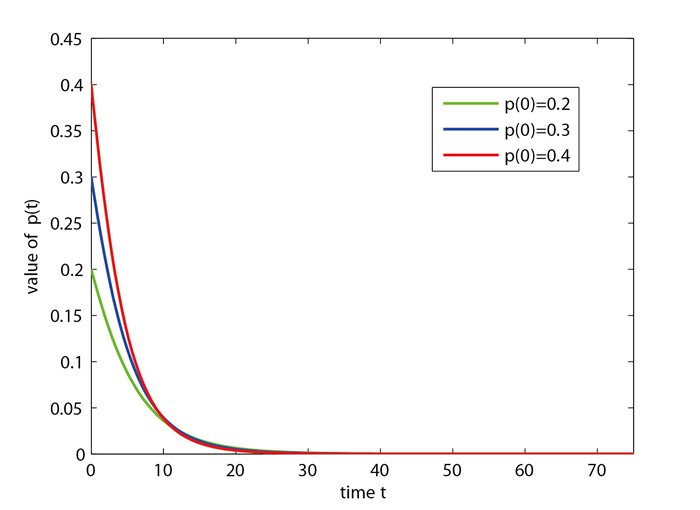
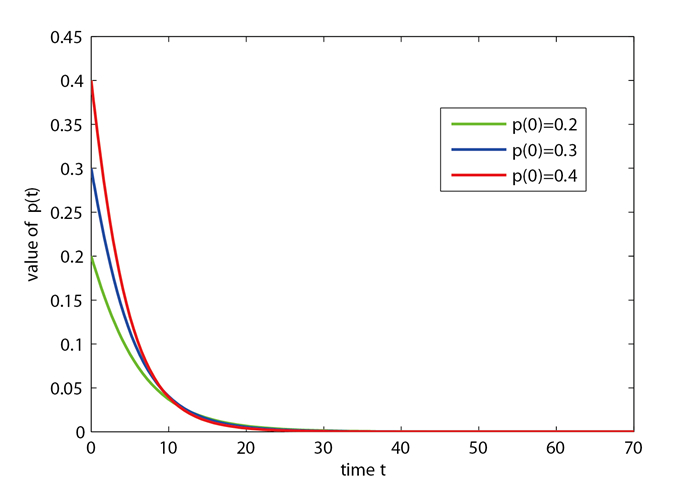
情况 2 线性系统(2.2)初始条件参数取值为
图 3
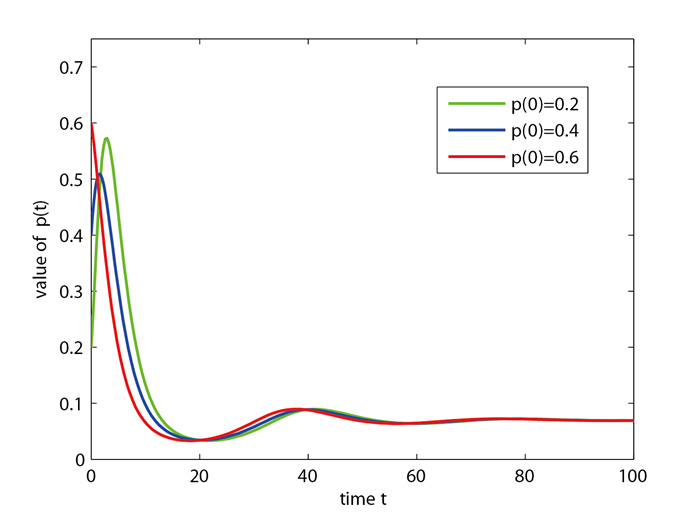
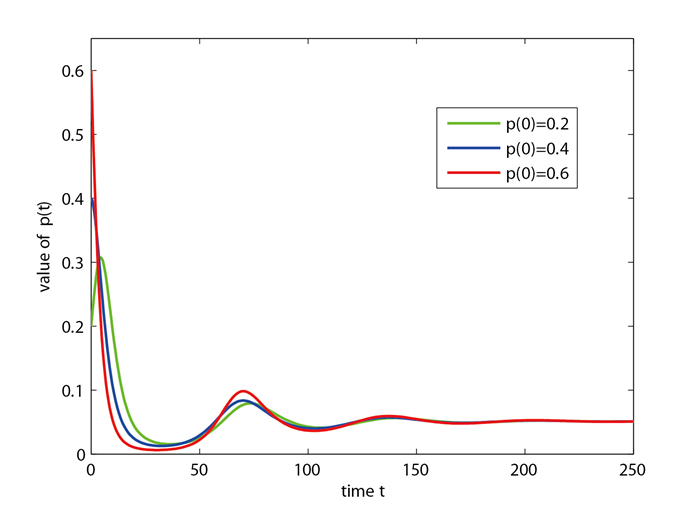
情况 3 线性系统(2.2)初始条件参数取值为
图 4
(2)将具有随机权重为
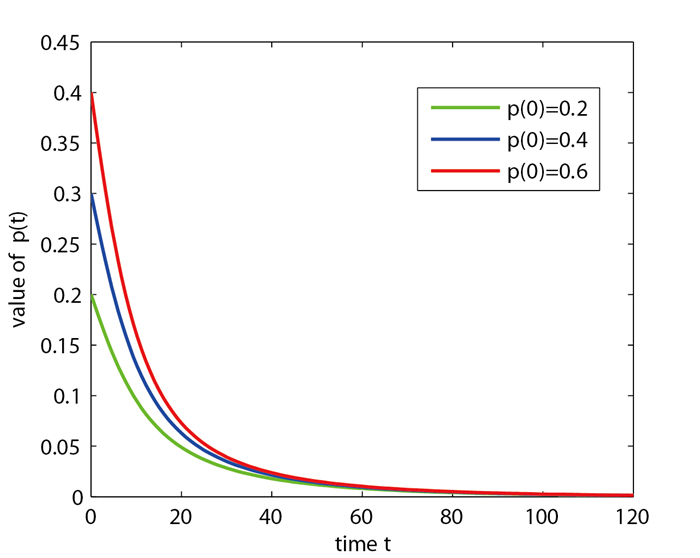
情况 4 非线性系统(2.1)初始条件参数取值为
图 5
情况 5 线性系统(2.2)初始条件参数取值为
图 6
情况 6 线性系统(2.2)初始条件参数取值为
图 7
(3)将有250个节点且边的权重受正态分布的影响,边权重的均值取0.5、权重的标准差为0.25的Barab6si-Albert(BA)无标度图作为传播网络.于是,
情况 7 非线性系统(2.1)初始条件参数取值为
图 8
情况 8 线性系统(2.2)初始条件参数取值为
图 9
情况 9 线性系统(2.2)初始条件参数取值为
图 10
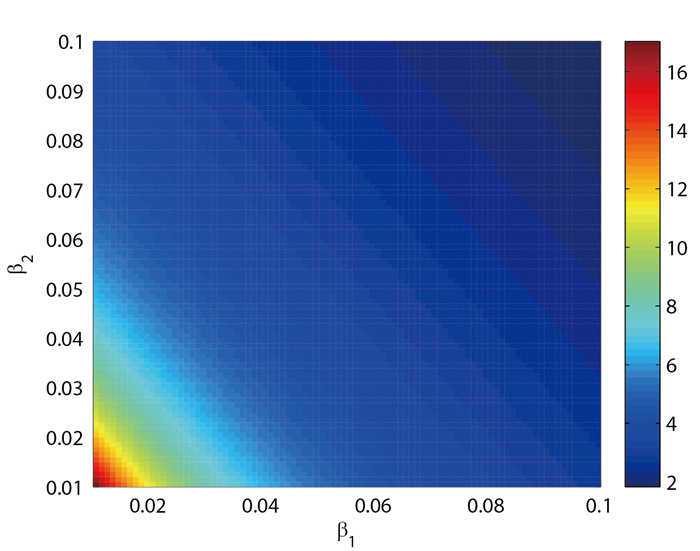
(4)传播阙值
图 11
图 12
从这些结果中,该文提出了以下控制计算机病毒传播的建议.
(a)通过防火墙过滤和阻止可疑消息,以降低感染率
(b)定期洁除计算机上的病毒,以提高治愈率
5 结论
该文旨在探讨广义网络对计算机病毒传播的影响.为此提出了一种新的非线性和新的线性计算机病毒传播模型.模型分析表明,网络的最大特征值是决定病毒流行的关键因素.于是据此给出了非线性和线性模型中无病毒平衡点的全局稳定性的充分条件.病毒平衡点在线性模型中的全局吸引力也得到了证实.最后,该文还给出了一些具体数值例子.
据我们所知,还有很多关于这个方向的工作尚未完成,例如:多层网络上的SLBRS模型;时变网络上的SLBRS模型,这些将是我们未来的研究工作.
参考文献
Computer viruses:Theory and experiments
A novel computer virus model and its dynamics
DOI:10.1016/j.nonrwa.2011.07.048 [本文引用: 1]
Modeling and analysis of the spread of computer virus
A propagation model of computer virus with nonlinear vaccination probability
Theoretical and experimental analysis of the impacts of removable storage media and antivirus software on viral spread
An epidemic model of computer viruses with vaccination and generalized nonlinear incidence rate
Dynamic model of worms with vertical transmission in computer network
The spread of computer viruses under the influence of removable storage devices
A new epidemic model of computer viruses
A novel computer virus propagation model and its dynamics
DOI:10.1080/00207160.2012.715388
A computer virus model with graded cure rates
DOI:10.1016/j.nonrwa.2012.07.005
The impact of patch forwarding on the prevalence of computer virus:A theoretical assessment approach
DOI:10.1016/j.apm.2016.10.028 [本文引用: 1]
Velocity and hierarchical spread of epidemic outbreaks in scale-free networks
DOI:10.1103/PhysRevLett.92.178701 [本文引用: 1]
Small but slow world:how network topology and burstiness slow down spreading
Behaviors of susceptible-infected epidemics on scale-free networks with identical infectivity
An SIS model with infective medium on complex networks
Modeling the propagation of mobile malware on complex networks
Global asymptotic stability and a property of the SIS model on bipartite networks
DOI:10.1016/j.nonrwa.2011.09.003
Modeling computer virus prevalence with a susceptible-infected-susceptible model with reintroduction
A note on the global behaviour of the network-based SIS epidemic model
DOI:10.1016/j.nonrwa.2007.04.001 [本文引用: 1]
Thresholds for epidemic spreading in networks
DOI:10.1103/PhysRevLett.105.218701 [本文引用: 1]
The impact of countermeasure propagation on the prevalence of computer viruses
Thresholds for Virus Spread on Networks
Epidemic outbreaks in complex heterogeneous networks
Epidemics of computer viruses:A complex-network approach
Virus spread in networks
DOI:10.1109/TNET.2008.925623 [本文引用: 1]
An individual-based approach to SIR epidemics in contact networks
DOI:10.1016/j.jtbi.2011.05.029 [本文引用: 1]
Predicting epidemics on directed contact networks
DOI:10.1016/j.jtbi.2005.10.004 [本文引用: 1]
Analysis of weighted networks
A deterministic model for gonorrhea in a nonhomogeneous population