1 引言
浅水波由Saint-Venant方程组[4]来描述,这个方程组大约在130年前就被提出来了,至今仍然广泛的应用于河流、湖泊或是海洋的水的流动.在一维的情形下, Saint-Venant方程组为
初始条件为
这里
我们主要考虑方程组的稳态解
在许多的实际应用当中,我们考虑其中一类特殊的稳态解称为"Lake at rest",也称为"静稳态解"
2 KP格式
KP格式也称为半离散的中心迎风格式
这里
中心迎风数值通量为
这里用以下通量记号
这里的值
这个解由分片线性重构给出
斜率限制器选择minmod限制器.
最后
为了和谐性,在不影响守恒性的同时,人们往往改用对自由面
如果
如果
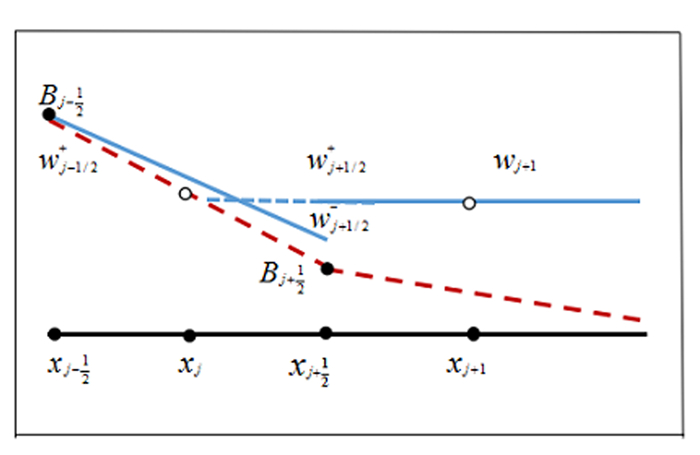
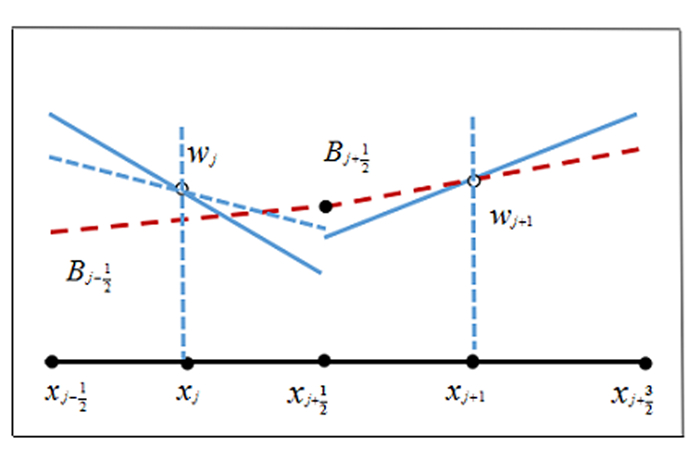
这种重构方法,虽然保证了在重构过程中水深非负性,但是在干湿界面附近的和谐性出现问题,这从图 2.1中可以体现.
图 2.1
因为如果满足
进而可以得到
3 BCKN格式
BCKN格式可以看作是KP格式的一个改进.在研究了KP格式之后,我们可以发现KP格式的不足之处是在干湿交错单元没有和谐性, BCKN格式解决了这个问题.接下来,我们研究BCKN格式的重构过程.
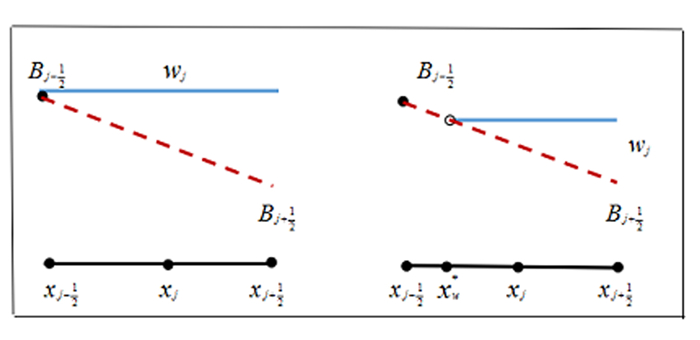
当出现干湿界面的情况时,中心迎风格式在重构阶段有可能使得格式产生负的水深, 图 3.1可以帮我们很好的理解这一点.为了叙述简单只考虑以下情形:
图 3.1
假设在某个几乎干的单元
而且在单元
也就是单元
计算单元
如果单元
否则是连续的分片线性函数
这样定义以后,在单元
其中
至此可以得到
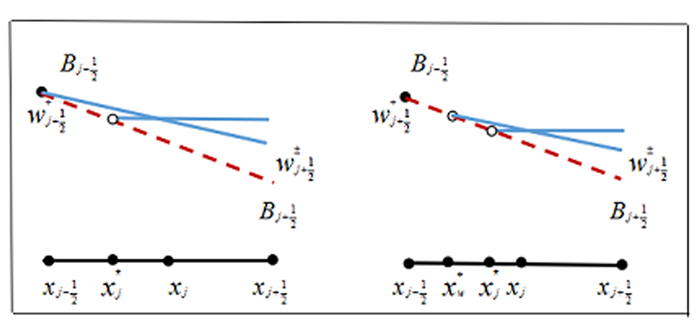
关于BCKN格式,在半淹没单元
可得
图 3.2
根据守恒性要求,如果
这里
综合两种情形我们可以得到重构的值
从重构的整个过程不难理解, BCKN格式的核心思想就是建立了
4 T格式
T格式虽然也是中心格式,但是与KP格式和BCKN格式都有着很大的区别. KP格式和BCKN格式使用的网格都是非交错网格,而T格式的网格则是交错网格,因为方程的解同样是分片线性的一个近似解,格式同样具有二阶精度. T格式的主要思想大致可以分为三个部分: "向前投影", "预测步", "向后投影".将方程
其中
通量满足
因为对方程的解进行了线性化处理,即
通过求解积分
从而可以得到"向前投影"
同理可以得到"向后投影"
通过对上式积分等式的处理我们可以得到交错网格上的中心格式
其中
源项的离散为
求解这个步骤还需要"预测步"
其中
T格式的修正过程为
为了叙述的简洁,省略时间记号并且我们只描述两种情形: (1)
第一种情形
如果
如果
第二种情形
如果
如果
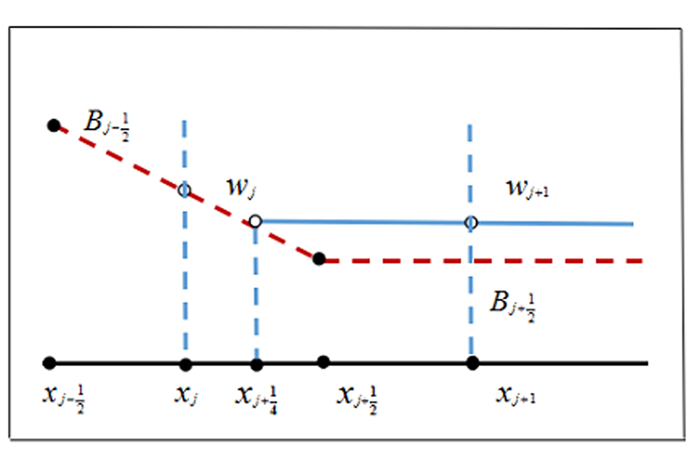
这样的修正的过程可以使得格式具有保正性,但是却破坏了和谐性.考虑如图 4.1中所示有下面定理.
图 4.1
定理4.1 考虑计算区域出现干湿界面:取
证 不妨假设
结论得证.
T格式在交错单元解的更新公式中关于源项的离散不能保证守恒性,如图 4.2中所示.水深的积分平均值
图 4.2
事实上水深的积分平均值为
基于以上两种原因易知格式不满足和谐性要求.
5 数值算例
我们在这一部分主要研究: KP格式, BCKN格式, T格式的部分应用.这里我们取KP格式和BCKN格式的斜率限制器为
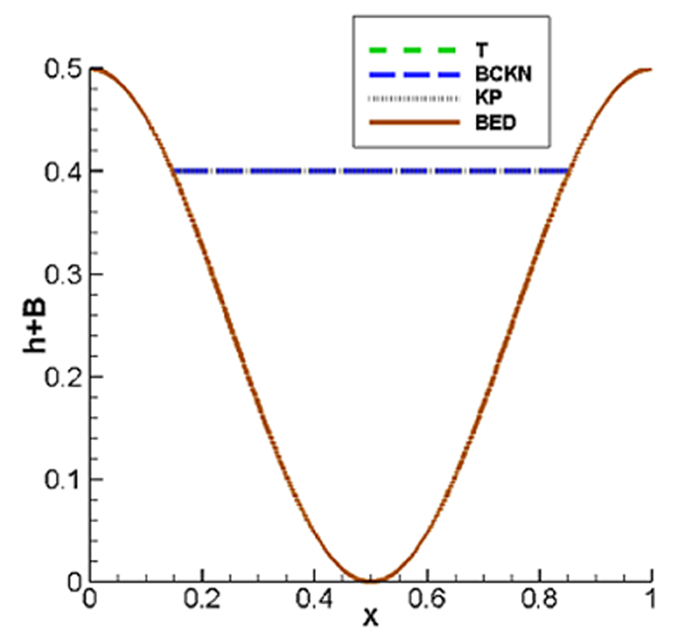
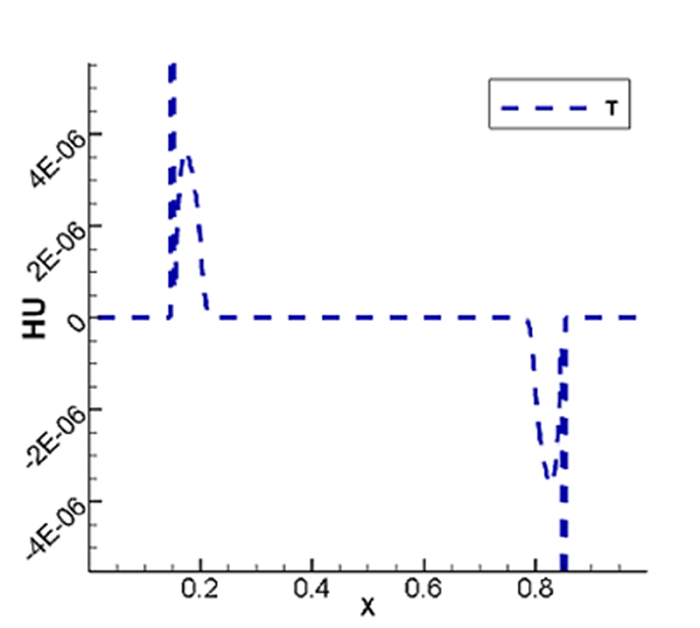
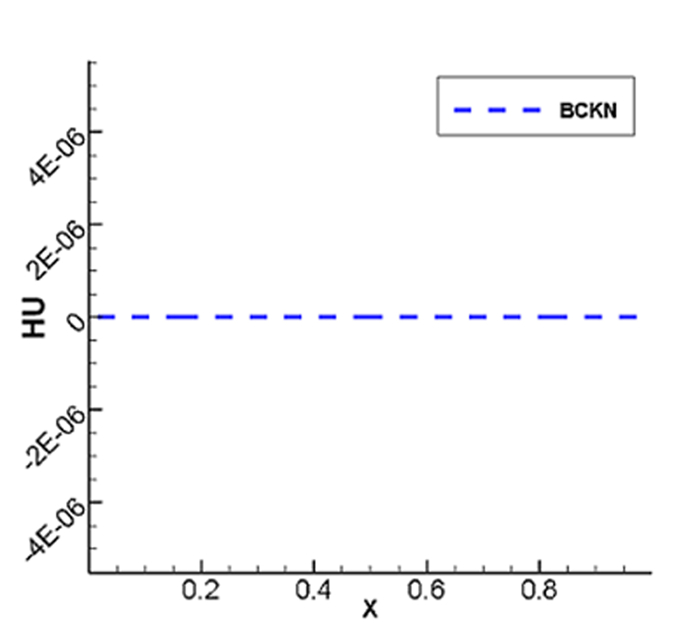
5.1 静水及其扰动
我们首先考虑静水情形,即在有水的部分
水深的初始值以及水的初始速度为
图 5.1
图 5.2
图 5.3
图 5.4
其次我们考虑当水面有一定扰动的情形.同样取底部函数为
水深的初始值以及水的初始速度为
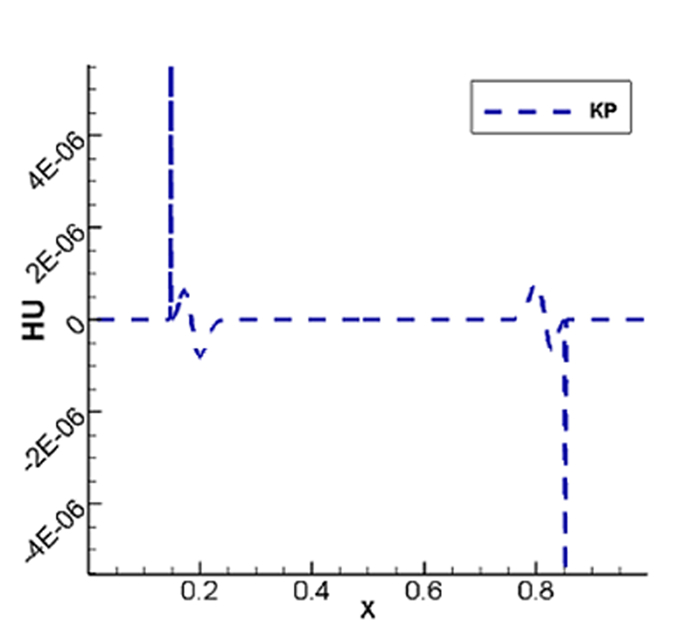
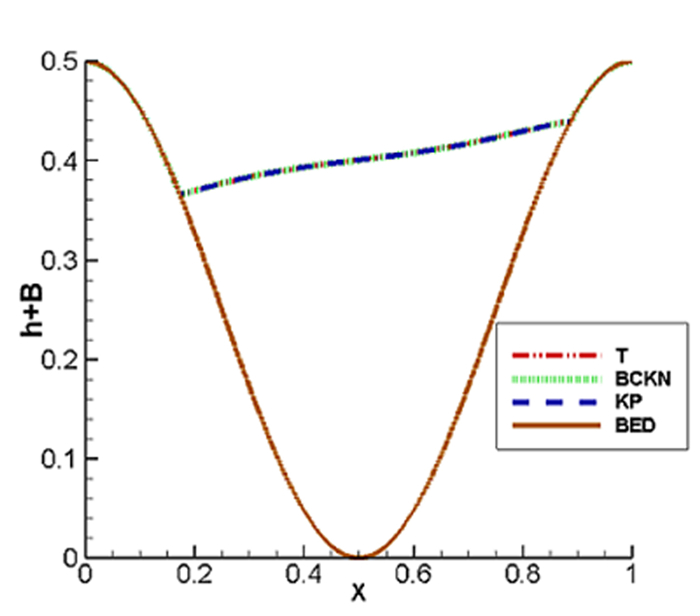
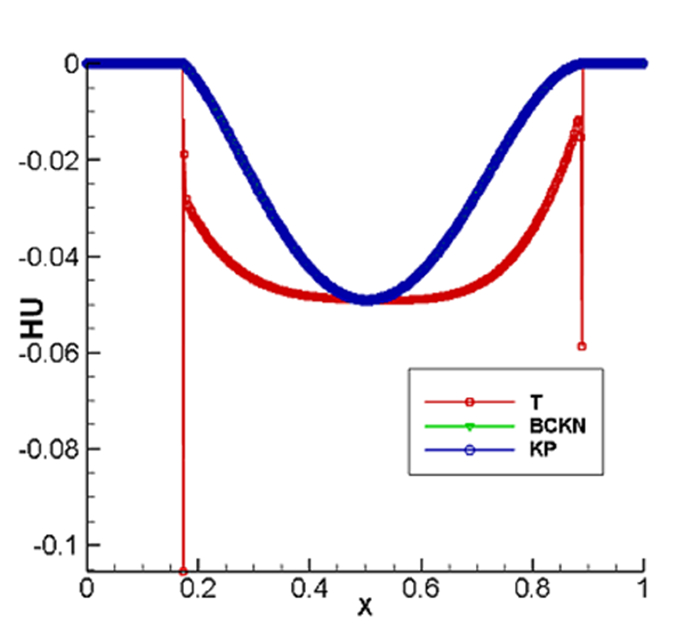
图 5.5
图 5.6
5.2 黎曼问题
在这一部分我们主要考虑以下黎曼问题.底部函数为
水的初始速度
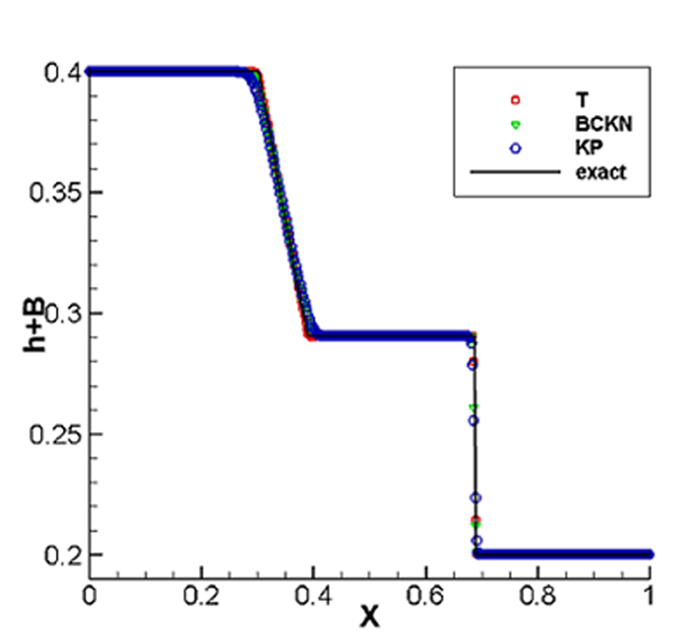
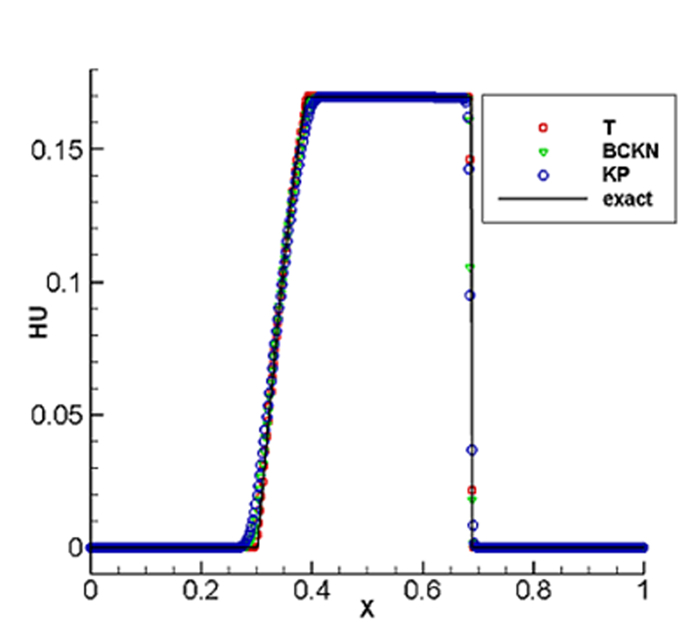
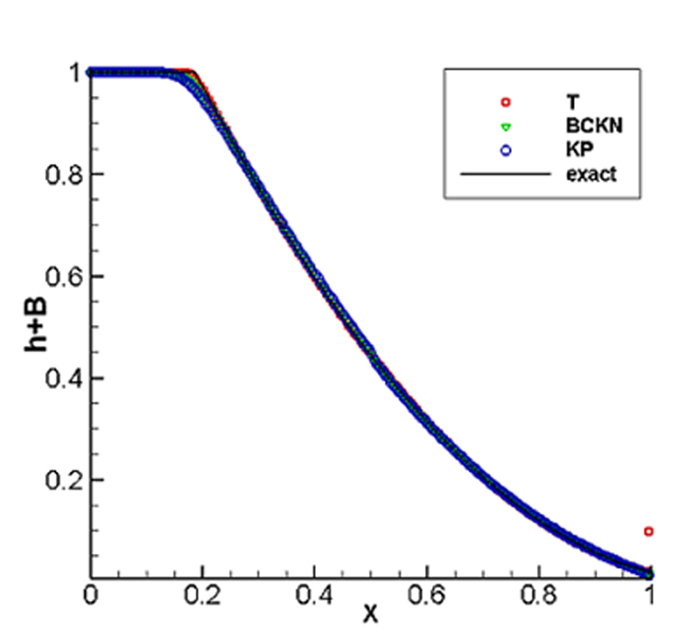
图 5.7
图 5.8
其次我们考虑以下黎曼问题.底部函数为
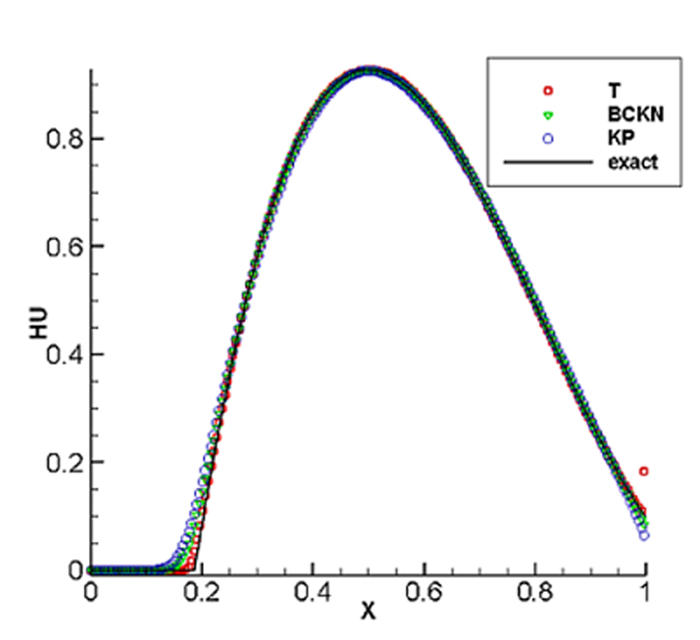
图 5.9
图 5.10
6 总结
论文总结研究了受关注的浅水波方程的离散格式: KP格式, BCKN格式, T格式. KP格式和BCKN格式中都需要局部速度的值,因此又称为中心-迎风格式. T格式可以看作是NT格式在带有源项的浅水波方程上的应用.我们在论文中主要是分析研究三种格式在求解带有源项的浅水波方程上时的优势以及不足之处.浅水波方程对于其数值格式有较高的要求,在实际应用中我们更关心在稳态解附近的行为,所以要求格式具有和谐性,特别是当计算区域出现干湿界面的时候需要保持水深恒为非负,同时又要求数值格式具有较高的精度.通过一些算例的展示我们可以看到BCKN格式可以满足所有的要求.这里需要特别指出的是我们在应用BCKN格式和KP格式时斜率限制器的选择为
参考文献
A second-order well-balanced positivity preserving central-upwind scheme for the saint-venant system
DOI:10.4310/CMS.2007.v5.n1.a6 [本文引用: 1]
A well-balanced reconstruction of wet/dry fronts for the shallow water equations
DOI:10.1007/s10915-012-9677-5 [本文引用: 1]
Well-balanced central schemes for systems of shallow water equations with wet and dry states
DOI:10.1016/j.apm.2015.09.073 [本文引用: 1]
Théorie du mouvement non permanent des eaux, avec application auxcrues des riviéres et à l'introduction des marées dans leur lit
On a well-balanced high-order finite volume scheme for the shallow water equations with bottom topography and dry areas
Finite volume evolution galerkin methods for the shallow water equations with dry beds
DOI:10.4208/cicp.220210.020710a
Central-upwind schemes for the saint-venant system
A kinetic scheme for the saint-venant system with a source term
Stabilized residual distribution for shallow water simulations
DOI:10.1016/j.jcp.2008.10.020 [本文引用: 1]
Well-balanced finite volume schemes of arbitrary order of accuracy for shallow water flows