1 引言
其中
的持久性和正平衡点的局部渐近稳定性和全局渐近稳定性等动力性质.在系统(1.2)中
在本文中,我们以时滞
2 准备工作
由系统(1.2)可知,除
的
成立,那么平衡点
在这一部分中我们主要给出系统正平衡点
令
线性化后是
其中
成立,则
由文献[15]中的引理4.1,引理4.2,定理4.1和注释4.1,我们有下面结论.
引理2.1 如果条件
成立,则当
引理2.2 (ⅰ)~若(H
成立且
(ⅱ)~若(H
成立且
引理2.2中的(ⅰ)、(ⅱ)两种情形表明当
和
定理2.1在系统(1.2)中,
(ⅰ) 若(H
(ⅱ) 若(H
(ⅲ) 若(H
记
为方程(2.5)的根满足
则下面的横截条件成立
需要注意的是,由sign
由定理2.1我们可以直接得出下面的定理.
定理2.2 在系统(1.2)中,时滞
3 Hopf分支
由第二部分的分析和定理2.2可知,
首先,通过引入无穷小生成元把时滞系统(1.2)转化为无穷维系统.需要下面两小步.
(ⅰ) 将系统(1.2)无量纲化.令
其中
令
由Riesz表现定理,存在一个
事实上,我们可以选择
也就是
则满足方程(3.2).
(ⅱ) 引入无穷小生成元.为了把时滞系统(1.2)转化为抽象常微分形式,我们引入无穷小的生成元
且
其中
则系统(1.2)等价于下面的算子方程
其中
其次,利用谱分解理论和无穷维系统的中心流行理论求出限制在中心流形上的流所满足的二维常微分方程.我们进行接下来的两小步.
(ⅰ) 引入
和一个双线性型
其中
我们知道
即
令
近而,由
(ⅱ) 得到二维常微分方程.与Hassard[16]用同样的符号标记,我们先计算刻画在
在中心流形
其中
对系统(1.2)的解
我们可以重新整理(3.8)式为
其中
再则,分析二维常微分方程且通过比较系数法求得这个二维常微分方程的系数.我们需要分(ⅰ)和(ⅱ)两小步得到(3.10)式的系数.
(ⅰ) 计算
其中
展开上述级数并进行系数比较后可得
由(3.8)和(3.9)式,令
由(3.7)式,我们有
且
其中
因此
由(3.14)式和
与(3.10)式比较系数,可得
因此,我们可以求出
(ⅱ) 计算
由(3.16)式,为了计算
我们讨论(3.11)式中
和
因此
由上式比较系数可得
且
由(3.17)式得
再由(3.3)式,可得
求解
利用同样的方法,由(3.18)式,我们有
再由(3.3)式,可得
求解
接下来,为了求
由(3.11)式,可得
因此
将(3.14)式代入上面等式中,比较
且
由
把(3.19)和(3.21)式代入(3.23)式中,有
由
可得
因此
由
把(3.20)和(3.22)式代入(3.25)式中可得
由(3.24)式,可得
因此
由
最后,得到hopf分支关于稳定性、方向和周期的特性.将有下面的(ⅰ)和(ⅱ)两小步去完成.
(ⅰ) 计算参数
(ⅱ) 因此,我们可以计算出参数
定理3.1 对系统(1.2)来说,下列结论成立
(1) 如果
(2) 如果
(3) 如果
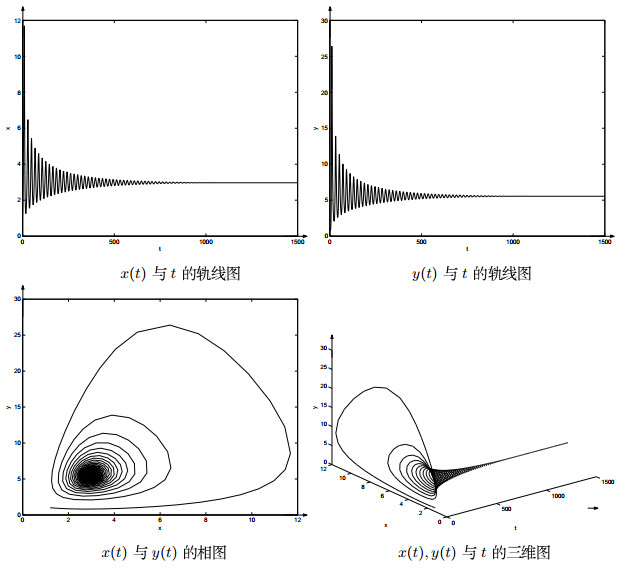
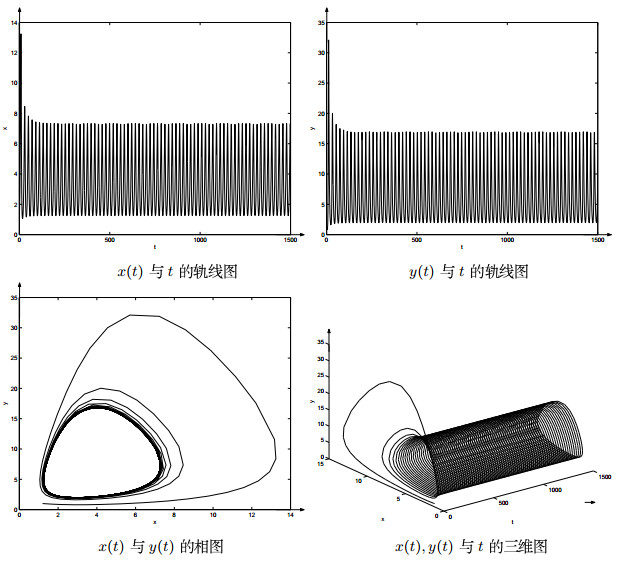
4 数值模拟
在这一部分中,我们将用数值模拟表明系统(1.2)有趣的动力行为.从下面例子可以看出,随着时滞
例4.1 令
通过数值计算,我们有
图 1
图 2
5 结论
在前期准备工作中得到:条件(H
参考文献
A time-delay model of single-species growth with stage structure
DOI:10.1016/0025-5564(90)90019-U [本文引用: 1]
Coupling in predator-prey dynamics:ratio-dependence
DOI:10.1016/S0022-5193(89)80211-5
Dynamics of the density dependent and nonautonomous predator-prey system with Beddington-DeAngelis functional response
DOI:10.3934/dcdsb
Uniqueness of periodic solutions of a nonautonomous density-dependent predator-prey system
DOI:10.1016/j.jmaa.2014.09.008
Bifurcation analysis in a predator-prey system with stage-structure and harvesting
DOI:10.1016/j.jfranklin.2010.03.017
Local Hopf bifurcation and global periodic solutions in a delayed predator-prey system
DOI:10.1016/j.jmaa.2004.06.056 [本文引用: 1]
Mutual interference between parasites or predators and its effect on searching efficiency
A model of trophic interaction
Functional response modified by predator density
DOI:10.1007/s00442-008-1225-5 [本文引用: 1]
Competition in populations of one age group
A model for a species with two life history stages and added mortality
DOI:10.1016/0304-3800(80)90081-2 [本文引用: 1]
Dynamics of the density dependent predator-prey system with Beddington-DeAngelis functional response
DOI:10.1016/j.jmaa.2010.08.029 [本文引用: 6]