1 引言
自1963年美国著名气象学家Lorenz在文献[1]中提出第一个三维自治混沌系统(即Lorenz系统)以来,混沌系统的构造与理论研究成为了非线性科学的热点问题,在这研究过程中众多三维混沌系统被相继提出,其中Chen系统[2]和Lü系统[3]是不得不提及的.在文献[4]意义下Chen系统是Lorenz系统的对偶系统, Lü系统则充当二者之间的桥梁角色.还有Sprott在1994年通过计算机搜索找出的19个三维混沌系统[5], Rössler系统[6]和Chua系统[7]也都受到了学者们的普遍关注.更多有关三维混沌系统的报道可以参看文献[8-10].大部分系统有1个平衡点或者2个对称平衡点或者3个平衡点,甚至更多,其共同特征是所有平衡点皆不稳定[11].在2008年, Yang和Chen[12]提出了一个具有一个鞍点和两个稳定结焦点的混沌系统[13]. Wei和Yang在文献[14]介绍了一类仅有两个稳定平衡点的混沌系统.值得注意的是,上述混沌系统有一个共同的特点,那就是两个对称的平衡点总是有相同的稳定性.在文献[15]中Liu等人提出一个新的三维混沌系统,
为了更深入了解系统(1.1)所生成的各类吸引子的几何结构,分析系统全局动力学特征,探究所生成混沌吸引子的几何机理,本文首先运用Poincaré紧致化技术来对系统(1.1)的无穷远动力学行为进行分析,然后通过添加线性反馈控制项
2 基本性质
在系统(1.1)中,
为了分析系统(1.1)的全局动力学行为,下面我们简单介绍三维Poincaré紧致化技术.
记系统(1.1)为如下形式
其中
它等价于多项式向量场
是
3 无穷远动力学
为了叙述方便,首先给出如下引理.
引理3.1[27] 考虑系统
假设方程
(1) 如果
(ⅰ) 对(2.1)式做变换
令
(3.2)式有两个零特征值为
令
计算得
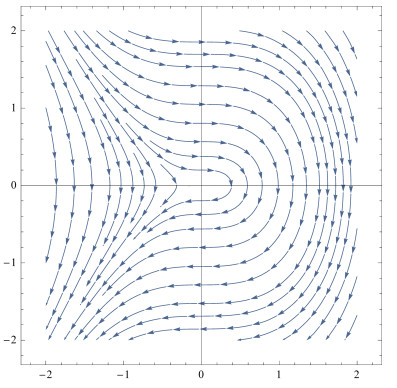
由引理3.1知,点
图 1
(ⅱ) 对(2.1)式做变换
如果令
显然,此方程组无解,即系统(1.1)在
(ⅲ) 对(2.1)式做变换
若令
系统(3.4)有唯一平衡点
设
有如下形式解
将(3.6)式代入(3.5)式,得
解以上方程可得
则(3.5)式的解为
将
由此知,
计算得
由上式可得,
且
综上所述,
由引理3.1知,点
图 2
4 异宿轨道
在这一节,我们设计一个控制器
值得注意,控制器
令
此系统的平衡点是一条线
特征值为
当
若
若
特别地,若
图 3
图 3
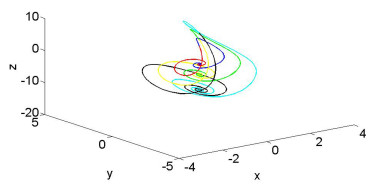
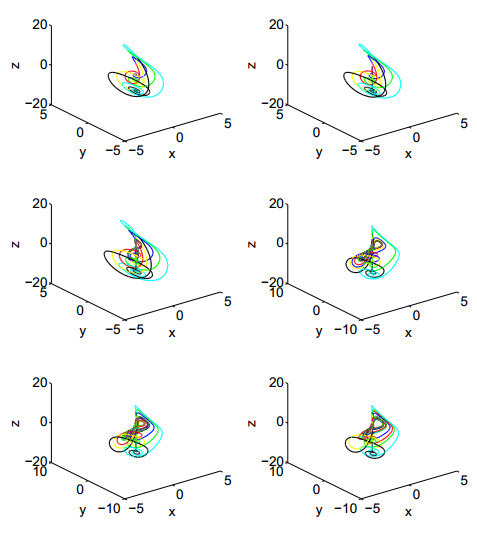
下面,我们取定
图 4
图 4
吸引子随着奇异异宿环的消失而产生,参数
从图 4中看出当参数
5 结论
为了深入了解系统混沌的几何机理,该文研究一类具有位置对称稳定性总是相反的新的混沌系统的全局动力学行为.基于
参考文献
Deterministic nonperiodic flow
DOI:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2 [本文引用: 1]
Yet another chaotic attractor
DOI:10.1142/S0218127499001024 [本文引用: 1]
A new chaotic attractor coined
DOI:10.1142/S0218127402004620 [本文引用: 1]
Control Systems:From Linear Analysis to Synthesis of Chaos
Some simple chaotic flows
DOI:10.1103/PhysRevE.50.R647 [本文引用: 1]
An equation for continuous chaos
DOI:10.1016/0375-9601(76)90101-8 [本文引用: 1]
The double scroll family
DOI:10.1109/TCS.1986.1085869 [本文引用: 1]
Analysis of a new chaotic system
DOI:10.1016/j.physa.2004.12.040 [本文引用: 1]
Analysis, control, synchronization, and circuit design of a novel chaotic system
A new 3D chaotic system with golden proportion equilibria:Analysis and electronic circuit realization
DOI:10.1016/j.compeleceng.2012.08.007 [本文引用: 1]
On a generalized Lorenz canonical form of chaotic systems
DOI:10.1142/S0218127402005467 [本文引用: 1]
A chaotic system with one saddle and two stable node-foci
DOI:10.1142/S0218127408021063 [本文引用: 1]
An unusual 3D autonomous quadratic chaotic system with two stable node-foci
DOI:10.1142/S0218127410026320 [本文引用: 1]
Dynamical analysis of a new autonomous 3-D chaotic system only with stable equilibria
DOI:10.1016/j.nonrwa.2010.05.038 [本文引用: 1]
An unusual chaotic system and its control
DOI:10.1016/j.mcm.2012.12.006 [本文引用: 2]
Intermittent and passivity based control strategies for a hyperchaotic system
DOI:10.1016/j.amc.2013.06.089 [本文引用: 1]
Singular orbits and dynamics at infinity of a conjugate Lorenz-like system
DOI:10.3846/13926292.2015.1019944
New results to a three-dimensional chaotic system with two different kinds of nonisolated equilibria
Controlling chaos
DOI:10.1103/PhysRevLett.64.1196 [本文引用: 1]
Optical cryptosystem based on synchronization of hyper-chaos generated by a delayed feedback laser diode
DOI:10.1103/PhysRevLett.80.2249
On feedback control of chaotic continuous-time systems
Nonlinear H.∞ synchronization of Lur'e systems:dynamic output feedback case
Feedback control methods for stabilizing unstable equilibrium points in a new chaotic system
Adaptive synchronization of two novel different hyperchaotic systems with partly uncertain parameters
不确定非线性系统的鲁棒自适应控制器
Robust adaptive controller for uncertain nonlinear system
Dynamics of the Lü system on the invariant algebraic surface and at infinity
DOI:10.1142/S0218127411029938 [本文引用: 1]