众所周知,多元正则变化能够使得随机向量${\bf X}$各个组成部分具有重尾性且按照相同的比例展示出极值行为,这保证了在其尾域存在渐近相依结构.特别地,总的超越的严重性可由尾指数$\alpha:=\sup\big\{\beta\geq 0: \textrm{E}||{\bf X}||^\beta<+\infty\big\}$来表示,该指数是一个将有限矩从无限矩分离出去的非负实数.此外,其尾部相依结构是由谱测度$\Psi$来刻画,此测度是单位球超越方向的渐近概率分布.作为结果,多元正则变化的假设使得我们能够根据相对于谱测度$\Psi$的积分表示尾相依系数以及其它很多相依特性.为了更多的细节,读者可参阅文献[5]和[1].

对于多元正则变化的随机损失向量${\bf X}$,文献[7]应用了极值风险指数去刻画投资组合损失的渐近性.众所知周,损失向量${\bf X}$的极值风险指数$\gamma_{{\bf w}}$是一个由投资组合权重向量${\bf w}$,尾指数$\alpha$和谱测度$\Psi$所表示的泛函,它度量了极值投资组合损失的敏感性并刻画了极值损失的概率分布的特征.特别地,由文献[7]可以看出极值风险指数$\gamma_{{\bf w}}$也可以被用来确定相对于极值投资组合损失的最优投资组合的分散.

为了比较相对于极值投资组合损失的多元概率分布,文献[8]给出了所谓的渐近投资组合损失(简记为APL)序.对于多元正则变化模型, APL序与根据极值风险指数$\gamma_{{\bf w}}$进行模型评价有关且可以被用来比较相对于多元极值投资组合损失模型的风险.在本文中,基于APL序,强渐近投资组合损失(简记为SAPL)序被提出. SAPL序可以通过所得到的相关极限而被应用到渐近量化极值投资组合的尾部概率的比值.在多元正则变化的相依结构下,我们得到了SAPL序的充分和必要准则,这些准则可以看做是对文献[8]对应结果的补充,完善和改进.这些得到的有关SAPL序的准则是由所涉及到的风险的尾部控制条件以及有关风险向量的正则化谱测度的一个积分序条件而组成. SAPL序的充分性准则的一个优点是极值投资组合损失的尾部概率的比值可以被渐近地量化.通过所得到的渐近比值,一个投资组合损失的风险价值可以被另一个投资组合损失的风险价值作近似估计,这在比较风险模型时具有实用性.另外一方面, SAPL序还被发现与相关的凸序及超模序有关.

本文的结构如下:部分2介绍了SAPL序并且和有关尾部概率的比值的极限做了一个简短的探讨.作为一个有趣的例子,我们给出了相对于椭球分布的SAPL序的充分性准则.为了便于参考,我们在部分3中简短地回顾了多元正则变化,谱测度与其正则标准化以及极值风险指数.部分4聚焦于多元正则变化随机风险向量.我们根据分量的SAPL序和一个正则化谱测度的恰当的序给出了SAPL序的充分和必要准则.此外,在SAPL序,凸序以及超模序之间的关系也被讨论.最后,在部分5中,我们通过一个例子例证了我们所得到的主要结果.

对于随机损失向量${\bf X}=(X_1, \cdots, X_d)\in\mathbb{R}^d$以及相关的单位简单形

$ \Sigma_d:=\bigg\{{\bf w}=(w_1, \cdots, w_d)\in \mathbb{R}_+^d: \sum\limits_{i=1}^d w_i=1\bigg\}$

上的投资组合向量${\bf w}$而言,投资组合损失被定义为${\bf w}^T {\bf X}=\sum\limits_{i=1}^d w_i X_i$.根据文献[8],一随机向量${\bf X}\in\mathbb{R}^d$以渐近投资组合损失(简记为APL)序比另一个随机${\bf Y}=(Y_1, \cdots, Y_d)\in\mathbb{R}^d$小,记为${\bf X}\le_{apl} {\bf Y}$,如果对于任意的${\bf w}\in \Sigma_d$,有

$ \limsup\limits_{t\to+\infty}\frac{P({\bf w}^T {\bf X}>t)}{P({\bf w}^T{\bf Y}>t)}\leq 1.$

在本文中,基于${\bf X}\le_{apl} {\bf Y}$之上,随机向量${\bf X}\in\mathbb{R}^d$以强渐近投资组合损失(简记为SAPL)序比随机向量${\bf Y}\in\mathbb{R}^d$小,对应地,记为${\bf X}\le_{sapl} {\bf Y}$,如果对于任意的${\bf w}\in \Sigma_d$,有

$ \lim\limits_{t\to+\infty}\frac{P({\bf w}^T {\bf X}>t)}{P({\bf w}^T {\bf Y}>t)}\le 1, $

其中按惯例$\frac{0}{0}=1$.

显而易见,强渐近投资组合损失序$\le_{sapl}$在分量按比例变换下保持不变.对于实向量${\bf v}=(v_1, \cdots, v_d)$与${\bf x}=(x_1, \cdots, x_d)$,令${\bf v}*{\bf x}=(v_1x_1, \cdots, v_dx_d)$.由于对于任意的${\bf v}\in \mathbb{R}_+^d$, ${\bf X}\le_{sapl}{\bf Y}$蕴含了${\bf v}*{\bf X}\le_{sapl}{\bf v}*{\bf Y}$,所以投资组合向量${\bf w}\in\Sigma_d$可以被等价地表示为${\bf w}\in \mathbb{R}_+^d$.在多元正则变化情形下,我们将根据$|X_1|\le_{sapl}|Y_1|, \cdots, |X_d|\le_{sapl}|Y_d|$以及随机向量${\bf X}$和${\bf Y}$的渐近相依结构的一个合适的序给出${\bf X}\le_{sapl}{\bf Y}$的充分性准则.

对于任意的投资组合${\bf w}\in \Sigma_d$,序关系${\bf X}\le_{sapl}{\bf Y}$断言了投资组合损失${\bf w}^T{\bf X}$以常用的随机序比投资组合损失${\bf w}^T{\bf Y}$小.此外,序关系${\bf X}\le_{sapl}{\bf Y}$还可以通过所涉及到的极限而被用于渐近量化极值投资组合损失${\bf w}^T{\bf X}$和${\bf w}^T{\bf Y}$的尾部概率的比值.显然, SAPL序只牵涉到极值投资组合损失.我们将在定理2.2中通过椭球分布来例证SAPL序.

现在,让我们建立一个有关两随机变量之间SAPL序的充分性准则的引理,此引理将在建立椭球分布间的SAPL序被用到.

又忆一非负随机变量$X$被称为具有尾指数$\alpha>0$正则变化的,记为$X\in {\rm RV}$或$X\in {\rm RV}_{\alpha}$,如果对于所有的$x>0$,都有$\lim\limits_{t\to +\infty}\frac{P(X>tx)}{P(X>t)}=x^{-\alpha}$.

引理2.1  假设一随机变量$V$独立于随机变量$R_i\in {\rm RV}_{\alpha}$, $i=1, 2$.若$R_1\le_{sapl}R_2$且对于某$\varepsilon>0$有${\rm E}(V)_{+}^{\alpha+\varepsilon}<+\infty$,则$R_1V\le_{sapl}R_2V$.

证  由于$R_i\in {\rm RV}_{\alpha}$以及对于某$\varepsilon>0$有${\rm E}(V)_{+}^{\alpha+\varepsilon}<+\infty$,故有

$ \lim\limits_{t\to+\infty}\frac{P(R_iV>t)}{P(R_1>t)}={\rm E}(V)_{+}^{\alpha}, \qquad i=1, 2.$

又由$R_1\le_{sapl}R_2$,我们有

$\lim\limits_{t\to+\infty}\frac{P(R_1>t)}{P(R_2>t)}\leq 1.$

把上面所得的关系式合并在一起可得

$\lim\limits_{t\to+\infty}\frac{P(R_1V>t)}{P(R_2V>t)}\leq 1.$

上式意味着$R_1V\le_{sapl}R_2V$.证毕.

一随机向量${\bf X}$被称为是服从椭球分布,记为${\cal E}({\bf \mu}, C, R)$,如果存在${\bf \mu}\in \mathbb{R}^d$和矩阵$A\in\mathbb{R}^{d\times d}$使得

${\bf X}\stackrel{d}{=}{\bf \mu}+RA{\bf U}, $

其中非负的$R$与在欧几里得球${\Bbb S}_2^d=\{{\bf s}\in \mathbb{R}^d: \|{\bf s}\|=1\}$上均匀分布的随机向量${\bf U}$是独立的.除了一常数因子外具有唯一性的矩阵$C\equiv AA^T$,由于$\textrm{Cov}({\bf X}) =\textrm{Var}(R)AA^T$,它还被称为随机向量${\bf X}$的广义协方差矩阵.易知${\rm E}\big(\|{\bf X}\|_2^2\big)<+\infty$等价于${\rm E}(R^2)<+\infty$.下面的定理给出了椭球分布间的序关系$\le_{sapl}$的充分性准则.

定理2.2  假设${\bf X}\sim {\cal E}({\bf \mu}_1, C_1, R_1)$和${\bf Y}\sim {\cal E}({\bf \mu}_2, C_2, R_2)$,其中$R_i\in {\rm RV}_{\alpha}$, $i=1, 2$.若${\bf \mu}_1\le{\bf \mu}_2$, $R_1\le_{sapl}R_2$以及对于任意的${\bf w}\in \Sigma_d$,有

(2.1) $ \begin{equation}\label{eqn2.7}{\bf w}^T C_1 {\bf w}\leq {\bf w}^T C_2 {\bf w}, \end{equation}$

则有

${\bf X}\le_{sapl}{\bf Y}.$

证  类似文献[8,定理2.7]的证明,不失一般性,我们假定${\bf \mu}_1={\bf \mu}_2={\bf 0}$.则对于任意的${\bf w}\in \Sigma_d$有

${\bf w}^T{\bf X}\stackrel{d}{=}R_1a_1{\bf v}_1{\bf U}\quad \mbox{和} \quad {\bf w}^T{\bf Y}\stackrel{d}{=}R_2a_2{\bf v}_2 {\bf U}, $

其中$a_i=\big({\bf w}^TC_i{\bf w}\big)^{1/2}$, ${\bf v}_i=a_i^{-1}A_i^T{\bf w}$, $i=1, 2$.由(2.1)式,我们可以更一步地假定$a_i>0$, $i=1, 2$.

由于${\bf v}_i^T{\bf v}_i=1$,故而${\bf v}_i^T{\bf U}$是${\bf U}\sim \textrm{unif}\big({\Bbb S}_2^d\big)$在单位长度向量上的正交投影.根据对称性, ${\bf v}_i^T{\bf U}\stackrel{d}{=}\|{\bf v}_i\|_2 U_1=U_1$的分布独立于${\bf v}_i$, $i=1, 2$,这意味着${\bf w}^T{\bf X}\stackrel{d}{=}a_1R_1U_1$和${\bf w}^T{\bf Y}\stackrel{d}{=}a_2R_2U_1$.根据$0<a_1\leq a_2$, $R_1\le_{sapl} R_2$以及引理2.1,我们有${\bf w}^T{\bf X}\le_{sapl}{\bf w}^T{\bf Y}$.证毕.

在给出主要结果之前,我们在这一部分给出多元正则变化,谱测度和其正则化以及极值风险指数的概念上的一个简介.

一随机向量${\bf X}\in\mathbb{R}^d$被称为是多元正则变化的(记为MRV),如果存在一序列$a_n\to +\infty$和在Borel $\sigma$ -域${\cal B}\big([-\infty, \infty]^d\ \backslash \{{\bf 0}\}\big)$上的一非零的Radon测度$\nu$使得$\nu\big([-\infty, +\infty]^d\ \backslash \mathbb{R}^d\ \big)=0$和${\bf X}/a_n$的概率分布函数$P_{{\bf X}/a_n}$在${\cal B}\big([-\infty, \infty]^d\ \backslash \{{\bf 0}\}\big)$上,当$n\to+\infty$时,满足

(3.1) $\begin{equation}\label{eqn3.1}nP_{{\bf X}/a_n}\stackrel{v}{\longrightarrow}\nu, \end{equation}$

其中$\stackrel{v}{\longrightarrow}$代表的是Radon测度的淡收敛.根据文献[5],一个椭球分布${\cal E}({\bf \mu}, C, R)$的多元正则变化等价于半径因子$R$的正则变化.

为了保证所有的资产损失$X_1, \cdots, X_d$与投资组合损失${\bf w}^T{\bf X}$的极值相关,除了(3.1)式以外,我们还假定测度$\nu$是非退化的,也就是

(3.2) $\begin{equation}\label{eqn3.2}\nu\big(\{{\bf x}\in \mathbb{R}^d: |x_i|>1\}\big)>0, \quad i=1, \cdots, d.\end{equation}$

注意到(3.1)式的极限测度$\nu$除了一个常数因子外具有唯一性,在集合$A_{\|\cdot\|}:=\{{\bf x}\in \mathbb{R}^d: \|x\|>1\}$上通过

(3.3) $ \begin{equation}\label{eqn3.3} \nu\big(A_{\|\cdot\|}\big)=1, \end{equation}$

其中$\|\cdot\|$是$\mathbb{R}^d$上的一个范数,极限测度$\nu$可以被标准化,另外,它在去掉向量${\bf 0}$的集合$A\in {\cal B}\big([-\infty, \infty]^d\ \backslash\{{\bf 0}\}\big)$上还展现了如下的成比例性质

(3.4) $\begin{equation}\label{eqn3.4}\nu(tA)=t^{-\alpha}\nu(A), \end{equation}$

其中指数$\alpha \in(0, +\infty)$对于每个随机向量${\bf X}$都是唯一的,从而被称为随机向量${\bf X}$的尾指数.其次,在上尾域满足(3.2)式的测度$\nu$也通过以下关系式

$P\big({\bf M}_n/a_n\in [-{\bf \infty}, {\bf x}]\big)\stackrel{w}{\longrightarrow}\exp\big\{-\nu\big([-\infty, \infty]^d\ \backslash [-{\bf \infty}, {\bf x}]\big)\big\}, \quad {{\bf x}\in (0, \infty]^d, }$

刻画分量方向上的极大值向量${\bf M}_n:=(M_{n, 1}, \cdots, M_{n, d})^T$的渐近分布,其中$M_{n, i}:=\max\{X_{1, i}, $$\cdots, X_{n, i}\}$, $i=1, \cdots, d$.故而$\nu$也被称为指数测度.为了获得更多的细节,读者可参阅文献[10-11]以及[3-4].

令$\tau({\bf x})=(\|{\bf x}\|, {\bf x}/\|{\bf x}\|)$是${\bf x}\in\mathbb{R}^d$相对于任意范数$\|\cdot\|$的极坐标.成比例性质(3.4)的一个直接结果是在

$\nu^\tau=c\rho_\alpha\otimes \Psi$

意义下有乘积表示$\nu^\tau=\nu\circ \tau$,其中$c>0$是一个常数,对于$x\in (0, \infty]$测度$\rho_\alpha((x, \infty]) =x^{-\alpha}$以及相对于范数$\|\cdot\|$在单位球${\Bbb S}_{\|\cdot\|}^d: =\{{\bf s}\in \mathbb{R}^d: \|{\bf s}\|=1\}$上的概率测度$\Psi$被称为$\nu$或${\bf X}$的谱测度.从现在开始,对于尾指数$\alpha$和谱测度$\Psi$的多元正则变化的随机向量${\bf X}$,我们把它记为${\bf X}\in {\rm MRV}_{\alpha, \Psi}$.对应于${\bf X}$的正则化谱测度$\nu^\ast$, $\Psi$的正则化版本被记为$\Psi^\ast$.由指数测度$\nu$可知,测度$\nu^\ast$对于$t>0$也有比例性质$\nu^\ast(tA)=t^{-1}\nu^\ast(A)$,从而也有如下的极坐标形式的乘积结构

$\nu^\ast \circ \tau^{-1}=\rho_1 \otimes \Psi^\ast,$

其中测度$\Psi^\ast$是${\bf X}$的正则化谱测度.

众所周知, ${\bf X}\in {\rm MRV}_{\alpha, \Psi}$蕴含着对于$\mathbb{R}^d$上任意范数$\|\cdot\|$都有$\|{\bf X}\|\in {\rm RV}_{\alpha}$.另外,根据文献[2],投资组合损失${\bf X}\in {\rm MRV}_{\alpha, \Psi}$意味着任意投资组合损失${\bf w}^T{\bf X}$都是正则变化的,其尾知数为$\alpha$.

令$\|\cdot\|_1$为和范数.对于与投资组合向量${\bf w}\in \Sigma_d$相关的随机向量${\bf X}\in {\rm MRV}$,其极值风险指数$\gamma_{{\bf w}}$可以被定义为

(3.5) $\begin{equation}\label{eqn3.5}\gamma_{{\bf w}}({\bf X})=\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big(\|{\bf X}\|_1>t\big)}.\end{equation}$

应用由(3.3)式标准化的$\nu$并利用其中的范数$\|\cdot\|$,我们有

$\gamma_{{\bf w}}({\bf X})=\nu\big(\big\{{\bf x}\in \mathbb{R}^d: {\bf w}^T{\bf x}>1\big\}\big), $

运用谱测度$\Psi$和尾指数$\alpha$,极值风险指数$\gamma_{{\bf w}}$还可以被表示为

$\gamma_{{\bf w}}({\bf X})=\int_{{\Bbb S}_1^d}({\bf w}^T{\bf s})_{+}^\alpha {\rm d}\Psi({\bf s}), \qquad{\bf w}\in \bigg\{{\bf x}\in \mathbb{R}^d: \sum\limits_{i=1}^{d}x_i=1\bigg\}.$

极值风险指数$\gamma_{{\bf w}}$可以被用来比较不同投资组合的风险,例如,可参阅文献[7].

为了研究极值投资组合损失的风险,我们在本部分研究了MRV结构下的SAPL序的充分和必要准则.

作为主要结论,定理4.2基于分量方向上的序$|X_i|\le_{sapl}|Y_i|$, $i=1, \cdots, d$以及随机向量${\bf X}$和${\bf Y}$的正则化谱测度的一个适当的序给出了${\bf X}\le_{sapl}{\bf Y}$的充分和必要准则.从所得到的与${\bf X}\le_{sapl}{\bf Y}$有关的极限,投资组合损失${\bf w}^T{\bf X}$的风险价值可由另一个投资组合损失${\bf w}^T{\bf Y}$所对应的风险价值做近似估计.此外,通过所得到的充分性准则,我们得到了在SAPL序,凸序和超模序之间的关系. SAPL序的必要性准则容许我们得到了有关正则化谱测度的序.

让我们从多元正则变化和SAPL序之间关系开始.

命题4.1  对于$\mathbb{R}^d$上的MRV随机向量${\bf X}$和${\bf Y}$,如果对任意的${\bf w}\in \Sigma_d$有$\lim\limits_{t\to+\infty} \frac{P(\|{\bf X}\|_1>t)}{P(\|{\bf Y}\|_1>t)}$$=0$和$\gamma_{{\bf w}}({\bf Y})>0$,那么

${\bf X}\le_{sapl}{\bf Y}.$

证  由极值风险指数的定义(3.5)可得

$\gamma_{{\bf w}}({\bf X})=\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big(\|{\bf X}\|_1>t\big)}\ \quad\mbox{和}\quad \gamma_{{\bf w}}({\bf Y})=\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf Y}>t\big)}{P\big(\|{\bf Y}\|_1>t\big)}.$

由以上结果, $\gamma_{{\bf w}}({\bf Y})>0$以及$\lim\limits_{t\to+\infty}\frac{P(\|{\bf X}\|_1>t)}{P(\|{\bf Y}\|_1>t)}=0$可推出

$\begin{eqnarray*}\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big({\bf w}^T{\bf Y}>t\big)}&=&\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big(\|{\bf X}\|_1>t\big)}\frac{P\big(\|{\bf Y}\|_1>t\big)}{P\big({\bf w}^T{\bf Y}>t\big)}\frac{P\big(\|{\bf X}\|_1>t\big)}{P\big(\|{\bf Y}\|_1>t\big)}\\&=&\frac{\gamma_{{\bf w}}({\bf X})}{\gamma_{{\bf w}}({\bf Y})}\lim\limits_{t\to+\infty}\frac{P\big(\|{\bf X}\|_1>t\big)}{P\big(\|{\bf Y}\|_1>t\big)}= 0, \end{eqnarray*}$

上式严格小于$1$,从而有${\bf X}\le_{sapl}{\bf Y}$.

注意到${\bf X}\in {\rm MRV}_{\alpha_1, \Psi_1}$和${\bf Y}\in {\rm MRV}_{\alpha_2, \Psi_2}$分别蕴含着$\|{\bf X}\|_1\in {\rm RV}_{\alpha_1}$和$\|{\bf Y}\|_1\in {\rm RV}_{\alpha_2}$.如果$\alpha_1>\alpha_2$,那么$\lim\limits_{t\to+\infty}\frac{P(\|{\bf X}\|_1>t)}{P(\|{\bf Y}\|_1>t)}=0$,于是由命题4.1立得${\bf X}\le_{sapl}{\bf Y}$.此外,根据命题4.1,具有相同尾指数$\alpha$的${\bf X}$和${\bf Y}$是研究相依结构对极值投资组合损失序的影响的基本环境.在MRV的结构下,尾域的渐进相依性的特征被谱测度$\Psi$或其正则版$\Psi^\ast$刻画,其中正则化谱测度$\Psi^\ast$在分量比例变换下保持不变.由于SAPL序在分量比例变换下也具有不变性,故而在刻画SAPL序特征时正则化谱测度$\Psi^\ast$被保留应用.由文献[8,命题3.2]知,对于满足(3.2)式的${\bf X}\in {\rm MRV}_{\alpha, \Psi}$有

$ \gamma_{{\bf w}}({\bf X})=\int_{{\Bbb S}_1^d}g_{{\bf w}, \alpha}({\bf vs}){\rm d}\Psi^\ast({\bf s}), $

其中$\Psi^\ast$是${\bf X}$的正则化谱测度,另外,还有分量为$v_i=\gamma_{{\bf e}_i}({\bf X})+\gamma_{{\bf -e}_i}({\bf X})$的比例向量${\bf v}=(v_1, \cdots, v_d)$和函数$g_{{\bf w}, \alpha}: \mathbb{R}^d\rightarrow \mathbb{R}$使得

$g_{{\bf w}, \alpha}({\bf x})=\bigg(\sum\limits_{i=1}^{d}w_i \cdot\Big((x_i)_{+}^{1/\alpha}-(x_i)_{-}^{1/\alpha}\Big)\bigg)_{+}^{\alpha}. $

更进一步,通过对所有的$i, j\in \{1, \cdots, d\}$都成立的平衡尾部条件

(4.1) $\begin{equation}\label{eqn4.2} \lim\limits_{t\to+\infty}\frac{P(|X_i|>t)}{P(|X_j|>t)}=1, \end{equation} $

文献[8,命题3.3(a)]断言对满足条件(4.1)的${\bf X}\in {\rm MRV}_{\alpha, \Psi}$有

(4.2) $ \begin{equation}\label{eqn4.3} \frac{\gamma_{{\bf w}}({\bf X})}{\gamma_{{\bf e}_1}({\bf X})+\gamma_{-{\bf e}_1}({\bf X})} =\int_{{\Bbb S}_1^d}g_{{\bf w}, \alpha}({\bf s}){\rm d}\Psi^\ast({\bf s}) =\Psi_{{\bf X}}^\ast g_{{\bf w}, \alpha}. \end{equation}$

由(4.2)式中的记号$\Psi^\ast g_{{\bf w}, \alpha}$,对任意的$g_{{\bf w}, \alpha}\in {\cal G}_\alpha$,积分序关系$\Psi^\ast\le_{{\cal G}_\alpha} \Phi^\ast$被定义为

$\Psi^\ast g_{{\bf w}, \alpha}\leq \Phi^\ast g_{{\bf w}, \alpha}, $

其中${\cal G}_\alpha:= \left\{g_{{\bf w}, \alpha}: {\bf w}\in \Sigma_d\right\}$, $\alpha>0$,而$\Psi^\ast$和$\Phi^\ast$是${\Bbb S}_1^d$上的正则化谱测度.

基于平衡尾部条件,分量间的SAPL序以及积分序关系$\le_{{\cal G}_\alpha}$,定理4.2给出了极值投资组合损失SAPL序的充分必要准则,而且此定理允许我们将随机向量间的$\le_{sapl}$降低到分量间的$\le_{sapl}$和正则化谱测度间的$\le_{{\cal G}_\alpha}$.

定理4.2  假设${\bf X}\in {\rm MRV}_{\alpha, \Psi_{{\bf X}}}$和${\bf Y}\in {\rm MRV}_{\alpha, \Psi_{{\bf Y}}}$对所有的$i, j\in \{1, \cdots, d\}$都满足如下的平衡尾部条件

(4.3) $\begin{equation}\label{bal}\lim\limits_{t\to+\infty}\frac{P(|X_i|>t)}{P(|X_j|>t)}=1\quad \mbox{和}\quad \lim\limits_{t\to+\infty}\frac{P(|Y_i|>t)}{P(|Y_j|>t)}=1.\end{equation}$

若$|X_1|\le_{sapl} |Y_1|$,则$\Psi_{{\bf X}}^*\le_{{\cal G}_\alpha}\Psi_{{\bf Y}}^*$蕴含着

${\bf X}\le_{sapl} {\bf Y}.$

反之,若${\bf X}\le_{sapl} {\bf Y}$和$|Y_1|\le_{sapl} |X_1|$,则

$\Psi_{{\bf X}}^\ast\le_{{\cal G}_\alpha}\Psi_{{\bf Y}}^\ast.$

证  根据(3.5)式, ${\bf X}$的尾部平衡条件和结论(4.2),我们有

$\begin{eqnarray*}\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big(|X_1|>t\big)}&=&\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big(\|{\bf X}\|_1>t\big)}\frac{P\big(\|{\bf X}\|_1>t\big)}{P\big(|X_1|>t\big)}\\&=&\gamma_{{\bf w}}({\bf X})\left[\lim\limits_{t\to+\infty}\frac{P\big(X_1>t\big)}{P\big(\|{\bf X}\|_1>t\big)}+\lim\limits_{t\to+\infty}\frac{P\big(-X_1>t\big)}{P\big(\|{\bf X}\|_1>t\big)}\right]^{-1}\\&= &\frac{\gamma_{{\bf w}}({\bf X})}{\gamma_{{\bf e}_1}({\bf X})+\gamma_{{\bf -e}_1}({\bf X})}\\&=&\Psi_{{\bf X}}^\ast g_{{\bf w}, \alpha}.\end{eqnarray*}$

类似地,我们也有

$\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf Y}>t\big)}{P\big(|Y_1|>t\big)}=\Psi_{{\bf Y}}^\ast g_{{\bf w}, \alpha}.$

将上述两个结果与$\Psi_{{\bf X}}^\ast\le_{{\cal G}_\alpha}\Psi_{{\bf Y}}^\ast$和$|X_1|\le_{sapl} |Y_1|$结合在一起可推得

$\begin{eqnarray*}\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big({\bf w}^T{\bf Y}>t\big)}&=&\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big(|X_1|>t\big)}\frac{P\big(|Y_1|>t\big)}{P\big({\bf w}^T{\bf Y}>t\big)}\frac{P\big(|X_1|>t\big)}{P\big(|Y_1|>t\big)}\\&=&\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big(|X_1|>t\big)}\\&&\cdot\lim\limits_{t\to+\infty}\frac{P\big(|Y_1|>t\big)}{P\big({\bf w}^T{\bf Y}>t\big)}\cdot\lim\limits_{t\to+\infty}\frac{P\big(|X_1|>t\big)}{P\big(|Y_1|>t\big)}\\&=&\frac{\Psi_{{\bf X}}^\ast g_{{\bf w}, \alpha}}{\Psi_{{\bf Y}}^\ast g_{{\bf w}, \alpha}}\cdot\lim\limits_{t\to+\infty}\frac{P\big(|X_1|>t\big)}{P\big(|Y_1|>t\big)}\\&\le& 1, \end{eqnarray*}$

这意味着${\bf X}\le_{sapl} {\bf Y}$.

另一方面,通过上述的讨论以及假设$|Y_1|\le_{sapl} |X_1|$,对$g_{{\bf w}, \alpha}\in {\cal G}_\alpha$,我们有

$\frac{\Psi_{{\bf X}}^\ast g_{{\bf w}, \alpha}}{\Psi_{{\bf Y}}^\ast g_{{\bf w}, \alpha}}=\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)}{P\big({\bf w}^T{\bf Y}>t\big)}\cdot\lim\limits_{t\to+\infty}\frac{P\big(|Y_1|>t\big)}{P\big(|X_1|>t\big)}\leq 1, $

这蕴含着$\Psi_{{\bf X}}^\ast\le_{{\cal G}_\alpha}\Psi_{{\bf Y}}^\ast$.证毕.

根据定理4.2的充分性准则,极限为$1$的$|X_1|\le_{sapl}|Y_1|$,也就是$\lim\limits_{t\to+\infty}\frac{P(|X_1|>t)}{P(|Y_1|>t)}=1$和$\Psi_{{\bf X}}^\ast\le_{{\cal G}_\alpha}\Psi_{{\bf Y}}^\ast$在${\bf X}\in {\rm MRV}_{\alpha, \Psi_{{\bf X}}}$, ${\bf Y}\in {\rm MRV}_{\alpha, \Psi_{{\bf Y}}}$以及${\bf X}$和${\bf Y}$满足所谓的平衡尾部条件下蕴含着${\bf X}\le_{sapl} {\bf Y}$.由于$\le_{sapl}$比$\le_{apl}$强,故而定理4.2的充分性准则改进了文献[8,定理3.6]的(b)部分的对应准则.此外,定理4.2中所得到的序${\bf X}\le_{sapl} {\bf Y}$可以用于风险的比较,也就是极限$\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)} {P\big({\bf w}^T{\bf Y}>t\big)}$可以被用于渐近量化极值投资组合损失的尾部概率的比值.

令$\textrm{VaR}_\beta(X):=\inf\big\{x: P(X\leq x)\geq \beta\big\}$表示随机损失$X$和置信水平$0<\beta<1$的风险价值.更进一步,由定理4.2和计算,我们可以直接得到下面的推论.

推论4.3  假设${\bf X}\in {\rm MRV}_{\alpha, \Psi_{{\bf X}}}$和${\bf Y}\in {\rm MRV}_{\alpha, \Psi_{{\bf Y}}}$满足平衡尾部条件(4.3).如果$|X_1|\le_{sapl} |Y_1|$,那么$\Psi_{{\bf X}}^*\le_{{\cal G}_\alpha}\Psi_{{\bf Y}}^*$蕴含着当$\beta\to 1$时,有

$P\big({\bf w}^T{\bf Y}> \textrm{VaR}_\beta\big({\bf w}^T{\bf X}\big)\big)\sim \frac{1-\beta}{c}, $

其中$0<c=\lim\limits_{t\to+\infty}\frac{P({\bf w}^T{\bf X}>t)}{P({\bf w}^T{\bf Y}>t)}\leq 1$以及$a(\beta)\sim b(\beta)$意味着$\lim\limits_{\beta\to 1}\frac{a(\beta)}{b(\beta)}=1$.

注4.4  由推论4.3知当$\beta$靠近$1$时有

$\textrm{VaR}_\beta\big({\bf w}^T{\bf X}\big)\approx \textrm{VaR}_{1-(1-\beta)/c}\big({\bf w}^T{\bf Y}\big).$

作为结果,当难以计算得到${\bf w}^T{\bf X}$的具体分布时,我们可以通过构造另一个容易计算风险价值的投资组合损失${\bf w}^T{\bf Y}$,对于$\beta$靠近$1$利用构造出的对应的风险价值$\textrm{VaR}_{1-(1-\beta)/c} \big({\bf w}^T{\bf Y}\big)$去估计$\textrm{VaR}_\beta\big({\bf w}^T{\bf X}\big)$.通过文献[9,推论2.3],对于$\beta\rightarrow 1$有

$\begin{eqnarray*}\textrm{VaR}_{1-(1-\beta)/c}\big({\bf w}^T{\bf Y}\big)&\sim& \frac{\gamma^{1/\alpha}_{{\bf w}}\big({\bf Y}\big)}{\gamma^{1/\alpha}_{{\bf e_1}}\big({\bf Y}\big)+\cdots+\gamma^{1/\alpha}_{{\bf e_d}}\big({\bf Y}\big)}\big(\textrm{VaR}_{1-(1-\beta)/c}\big(Y_1\big)\\&&+\cdots+\big(\textrm{VaR}_{1-(1-\beta)/c}\big(Y_d\big)\big).\end{eqnarray*}$

从而当$\beta$靠近$1$时,我们有

$\textrm{VaR}_{\beta}\big({\bf w}^T{\bf X}\big)\approx \frac{\gamma^{1/\alpha}_{{\bf w}}\big({\bf Y}\big)}{\gamma^{1/\alpha}_{{\bf e_1}}\big({\bf Y}\big)+\cdots+\gamma^{1/\alpha}_{{\bf e_d}}\big({\bf Y}\big)}\\\big(\textrm{VaR}_{1-(1-\beta)/c}\big(Y_1\big)+\cdots+\big(\textrm{VaR}_{1-(1-\beta)/c}\big(Y_d\big)\big).$

接下来,我们回顾一个有用的引理,此引理体现了MRV的随机损失向量的最好和最糟糕的可能的分散效果.

引理4.5^[8]  对于在$\Sigma_d$上的任一正则化谱测度$\Psi^\ast$, $\Psi_0^\ast:=\sum\limits_{i=1}^d \delta_{{\bf e}_i}$和$\Psi_1^\ast:=d\cdot\sum\limits_{i=1}^d \delta_{(1/d, \cdots, 1/d)}$,有

(ⅰ)当$\alpha\geq 1$时, $\Psi_0^\ast\le_{{\cal G}_\alpha}\Psi^\ast\le_{{\cal G}_\alpha}\Psi_1^\ast$;

(ⅱ)当$0<\alpha\leq 1$时, $\Psi_1^\ast\le_{{\cal G}_\alpha}\Psi^\ast\le_{{\cal G}_\alpha}\Psi_0^\ast$.

下面的推论可直接由定理4.2和引理4.5推得.

推论4.6  假设${\bf X}\in \mathbb{R} _+^d$是MRV的,其尾指数$\alpha\in (0, +\infty)$并有相同的一元边际分布$F$, ${\bf Y}$的各个边际是独立的且有相同的分布$F$,并且${\bf Z}$的边际是同单调的且有相同的分布$F$.则

(ⅰ)当$\alpha\geq 1$时, ${\bf Y}\le_{sapl}{\bf X}\le_{sapl}{\bf Z}$;

(ⅱ)当$0<\alpha\leq 1$时, ${\bf Z}\le_{sapl}{\bf X}\le_{sapl}{\bf Y}$.

引理4.7  假设${\bf X}$和${\bf Y}$在$\mathbb{R}^d$上是MRV的,它们有相同的尾指数$\alpha\neq 1$并满足平衡尾部条件(4.3).

(ⅰ)对于$\alpha>1$有$\Psi_{{\bf X}}^\ast\le_{{\cal G}_\alpha}\Psi_{{\bf Y}}^\ast$,如果对于任意的${\bf w}\in \Sigma_d$有$ \limsup\limits_{u\to+\infty} \frac{{\rm E}({\bf w}^T{\bf X}-u)_+}{{\rm E}({\bf w}^T{\bf Y}-u)_+}\leq 1$和

(4.4) $ \begin{equation}\label{eqn4.4} \limsup\limits_{t\to+\infty}\frac{P(|X_1|>t)}{P(|Y_1|>t)}=1; \end{equation}$

(ⅱ)对于$\alpha<1$有$\Psi_{{\bf Y}}^\ast\le_{{\cal G}_\alpha}\Psi_{{\bf X}}^\ast$,如果$\lim\limits_{t\to+\infty}\frac{P(|X_1|>t)}{P(|Y_1|>t)}=1$以及对于任意的${\bf w}\in \Sigma_d$有$\limsup\limits_{u\to+ \infty}\frac{{\rm E}[({\bf w}^T{\bf X})_{+}\wedge u]}{{\rm E}[({\bf w}^T{\bf Y})_{+}\wedge u]}\geq 1$.

基于引理4.7和定理4.2,我们可以得到SAPL序,凸序以及超模序之间的关系.关于凸序和超模序的相关定义可参阅文献[8].

推论4.8  ${\bf X}\le_{sapl}{\bf Y}$如果(ⅰ) ${\bf X}$和${\bf Y}$满足引理4.7 (ⅰ)的条件,其中条件(4.4)被$\lim\limits_{t\to+\infty}\frac{P(|X_1|>t)}{P(|Y_1|>t)}=1$代替,或者(ⅱ) ${\bf X}$和${\bf Y}$满足引理4.7 (ⅱ)的条件.

定理4.2的充分性准则可以被用于给多MRV椭球分布间的正则化谱测度排序.考虑随机向量${\bf X}\stackrel{d}{=}RA_1{\bf U}$和${\bf Y}\stackrel{d}{=}RA_2{\bf U}$,其中非负随机变量$R\in {\rm RV}_{\alpha}$($0<\alpha<+\infty$)与向量${\bf U}$独立,并且$d$ -维正定矩阵$C_i=A_iA_i^T$, $i=1, 2$满足条件(2.1),其中对角线元素为$c_{i, i}$, $i=1, \cdots, d$.于是由定理2.2,我们有${\bf X}\le_{sapl}{\bf Y}$.由SAPL序在分量比例变换下不变性,对于${\bf w}=(w_1, \cdots, w_d)$我们有${\bf wX}\le_{sapl}{\bf wY}$,其中$w_i=c_{i, i}^{-1/2}$, $i=1, \cdots, d$.其次,由文献[8,命题3.10]的证明过程,对于$i, j\in \{1, \cdots, d\}$有$w_iX_i\stackrel{d}{=}w_jY_j$.所以,由定理4.2的必要性准则和正则化谱测度在分量比例变换下的不变性,我们有

$\Psi_{{\bf X}}^\ast(\alpha, C_1)=\Psi_{{\bf wX}}^\ast\le_{{\cal G}_\alpha}\Psi_{{\bf wY}}^\ast=\Psi_{{\bf Y}}^\ast(\alpha, C_2), $

也就是$\Psi_{{\bf X}}^\ast(\alpha, C_1)\le_{{\cal G}_\alpha} \Psi_{{\bf Y}}^\ast(\alpha, C_2)$.这也是文献[8,命题3.10]的结论.

对于非平衡尾部的随机向量,则由定理4.2和$\le_{sapl}$在分量再比例下的不变性我们可直接得到下面的推论.

推论4.9  假设${\bf X}\in {\rm MRV}_{\alpha, \Psi_{{\bf X}}}$满足条件(3.2)和${\bf Y}\in {\rm MRV}_{\alpha, \Psi_{{\bf Y}}}$有平衡尾部.如果存在${\bf v}\in (0, \infty)^d$使得${\bf vX}$有平衡尾部, $|v_1X_1|\le_{sapl}|Y_1|$以及条件${\bf X}\le_{sapl}{\bf vX}$或${\bf Y} \le_{sapl}{\bf vY}$被满足,那么$\Psi_{{\bf X}}^\ast\le_{{\cal G}_\alpha} \Psi_{{\bf Y}}^\ast$蕴含着${\bf X}\le_{sapl}{\bf Y}$.

最后一个结果是基于谱测度$\Psi^\ast$和$\Phi^\ast$在$\Sigma_d$上的序$\le_{{\cal G}_1}$的一致性: $\Psi^\ast\le_{{\cal G}_1}\Phi^\ast$和$\Phi^\ast\le_{{\cal G}_1}\Psi^\ast$.谱测度在$\Sigma_d$上的这种特殊性使得将随机向量间SAPL序降为它们对应坐标间的SAPL序成为可能.

命题4.10  对于$\mathbb{R}_+^d$上尾指数为$\alpha=1$的MRV的${\bf X}$和${\bf Y}$,如果${\bf Y}$满足条件(3.2),那么$X_i\le_{sapl}Y_i$, $i=1, \cdots, d$蕴含着${\bf X}\le_{sapl}{\bf Y}$.

证  文献[6,引理5.22]的证明知:

(ⅰ)不失一般性,令${\bf Y}$有平衡尾部,再由$X_i\le_{sapl}Y_i$可推出

$\lambda_i=\lim\limits_{t\to+\infty}\frac{P(X_i>t)}{P(Y_i>t)}=\lim\limits_{t\to+\infty} \frac{P(X_i>t)}{P(Y_1>t)}\leq 1, \qquad i=1, \cdots, d;$

(ⅱ)对于${\bf w}\in \Sigma_d$,极值风险指数

$\gamma_{{\bf w}}({\bf X})=\sum\limits_{i=1}^d w_i\gamma_{{\bf e}_i}({\bf X})\leq \gamma_{{\bf e}_j}({\bf X}), $

其中$j=\arg\max\limits_{i=1, \cdots, d}\gamma_{{\bf e}_i}({\bf X})$,并且极值风险指数

$\gamma_{{\bf w}}({\bf Y})=\sum\limits_{i=1}^d w_i\gamma_{{\bf e}_i}({\bf Y})= \gamma_{{\bf e}_1}({\bf Y}).$

将上面两点联合起来,我们有

$\begin{eqnarray*}&&\lim\limits_{t\to+\infty}\frac{P({\bf w}^T{\bf X}>t)}{P({\bf w}^T{\bf Y}>t)}\\&=&\lim\limits_{t\to+\infty}\frac{P({\bf w}^T{\bf X}>t)}{P(X_j>t)}\cdot\frac{P\big(X_j>t\big)}{P(Y_1>t)}\cdot\frac{P(Y_1>t\big)}{P({\bf w}^T{\bf Y}>t)}\\&=&\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T{\bf X}>t\big)/P\big(\|{\bf X}\|_1>t\big)}{P\big(X_j>t\big)/P\big(\|{\bf X}\|_1>t\big)}\cdot\frac{P\big(X_j>t\big)}{P\big(Y_1>t\big)}\\&&\cdot\frac{P\big(Y_1>t\big)/P\big(\|{\bf Y}\|_1>t\big)}{P\big({\bf w}^T{\bf Y}>t\big)/P\big(\|{\bf Y}\|_1>t\big)}\\&=&\frac{\gamma_{{\bf w}}({\bf X})}{\gamma_{{\bf e}_j}({\bf X})}\cdot \lambda_j\cdot \frac{\gamma_{{\bf e}_1}({\bf Y})}{\gamma_{{\bf w}}({\bf Y})}\\&=&\lambda_j\cdot\frac{\gamma_{{\bf w}}({\bf X})}{\gamma_{{\bf e}_j}({\bf X})}\\&\le &\lambda_j\le 1, \end{eqnarray*}$

上式蕴含着${\bf X}\le_{sapl}{\bf Y}$.

在本部分,我们给出一例,用它例证我们的主要结果定理4.2.

例5.1  若随机向量${\bf X}\in \mathbb{R}^d$依分布等于$\mu+\sqrt{\alpha/W}{\bf Z}$,其中随即向量${\bf Z}\sim {\cal N}(0, C)$与随机变量$W\sim \chi_\alpha^2$是独立的,则${\bf X}$服从位置参数为$\mu$,自由度为$\alpha>0$以及广义协差阵为$C$的多元学生- $t$分布.此为,随即向量${\bf X}$也是椭球分布的并且还是尾指数为$\alpha$的MRV.

令二元随即向量${\bf X}$和${\bf Y}$服从自由度为$\alpha>0$,广义协差阵分别为$C_{\rho_1}$和$C_{\rho_2}$的学生- $t$分布,其中

$C_{\rho_i}=\Bigg( \begin{array}{cc}1&\rho_i\\\rho_i&1\end{array} \Bigg), \qquad i=1, 2.$

如果$\rho_1< \rho_2$,那么由文献[8,命题3.10]所得的$\Psi_{{\bf X} }^\ast\le_{{\cal G}_\alpha}\Psi_{{\bf Y}}^\ast$和定理4.2,我们有${\bf X}\le_{sapl}{\bf Y}$,此结果明显比文献[8,例5.3]所得到的结果${\bf X}\le_{apl}{\bf Y}$更强.

接下来,为了经验性地例证SAPL序,我们将进行蒙特卡罗模拟.为此,我们将利用上述提到的二元学生- $t$分布并分别从两个总体中随机产生两个一百万的样本,然后经验性地确定这两个模拟的总体间有SAPL序的存在.具体的细节如下.

(ⅰ)考虑两个随机向量${\bf X}\sim \sqrt{3/W_1}{\bf Z}_1$和${\bf Y}\sim \sqrt{3/W_2}{\bf Z}_2$,其中对于$i=1, 2$, $W_i\sim \chi^2_{3}$和${\bf Z}_i\sim N({\bf 0}, C_{\rho_i})$是相互独立的,并且$\rho_1=0.1<\rho_2=0.3$.

(ⅱ)相对于自由度为$3$的两个卡方分布和两个均值为零向量、协方差阵为$C_{0.1}$和$C_{0.3}$二元正态分布,我们随机地产生容量为一百万样本${\bf x}_i$和${\bf y}_i$, $i=1, 2, \cdots, 10^6$,从而得到了两个期待的服从二元学生-$t$分布的样本.

(ⅲ)产生下面的单位简单形

$\Sigma_{2}=\left\{(w_{1}, w_{2})^T\in\mathbb{R}_+^2:w_{1}+w_{2}=1\right\}, $

并令$w_{1}=0.5$以及$w_{2}=0.5$.

(ⅳ)计算模拟样本${\bf x}_1, \cdots, {\bf x}_{10^6}$在概率$\beta = 0.9930, 0.9901, \cdots, 0.9970$处的样本分位数$\widehat {\textrm{VaR}}_{\beta} ({\bf w}^T{\bf X})$,从而得到了对于$i=1, 2, \cdots, 10^6$处的事件$(w_{1}, w_{2}) \cdot{\bf y}_i>\widehat {\textrm{VaR}}_{\beta}({\bf w}^T{\bf X})$样本频率$\frac{1}{10^6}\sum\limits_{i=1}^{10^6}I\big({\bf w}^T{\bf y}_{i}>\widehat {\textrm{VaR}}_{\beta}({\bf w}^T{\bf X})\big)$.

(ⅴ)在最后一步,我们计算$\frac{1}{10^6}\sum\limits_{i=1}^{10^6}I \big({\bf w}^T{\bf x}_{i}>\widehat {\textrm{VaR}}_{\beta}({\bf w}^T{\bf X}) \big)$和样本频率$\frac{1}{10^6}\sum\limits_{i=1}^{10^6}{\rm I} \big({\bf w}^T{\bf y}_{i}>\widehat {\textrm{VaR}}_{\beta}({\bf w}^T {\bf X})\big)$在概率$\beta = 0.9930, 0.9901, \cdots, 0.9970$处的比值.

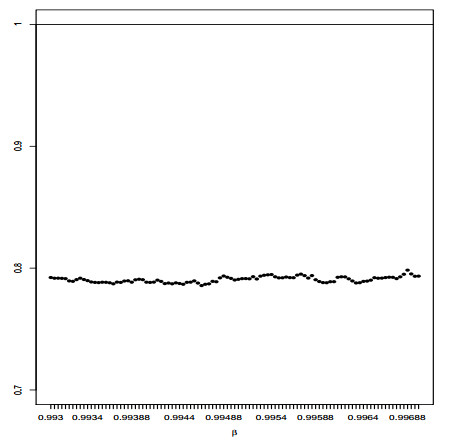
在图 1中,我们在单位简单形上做出了上述在最后一步所得到的比值所对应的点.如图所见,当$\beta$由$0.9930$递增到$0.9970$时,所得到的点稳定在水平线$0.8$以下.这经验性地验证了${\bf X}\le_{sapl}{\bf Y}$的存在.

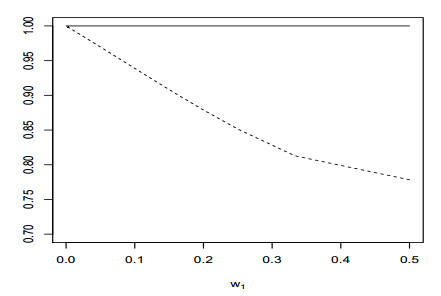
最后,我们给出一个渐近比值的具体的表达式.由文献[9]可得

$\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T {\bf X}>t\big)}{P(X_1>t)}=\left(\frac{{\bf w}^T C{\bf w}}{C_{11}}\right)^{\alpha/2}, \qquad {{\bf w}\in \Sigma_2.}$

因此不但${\bf X}\le_{sapl}{\bf Y}$可以被验证,而且它的相关的渐近比值也可以被清晰地表示出来.事实上,由上述极限我们有

$\lim\limits_{t\to+\infty}\frac{P\big({\bf w}^T {\bf X}>t\big)}{P\big({\bf w}^T {\bf Y}>t\big)}=\left(\frac{{\bf w}^T C_1{\bf w}}{{\bf w}^T C_2{\bf w}} \right)^{\alpha/2}=\left(\frac{w_1^2+w_2^2+2\rho_1w_1w_2}{w_1^2+w_2^2 +2\rho_2w_1w_2}\right)^{\alpha/2}.$

令$\alpha=3$, $\rho_1=0.1$, $\rho_2=0.3$, ${\bf w}_1=(1/5, 4/5)^T$, ${\bf w}_2=(1/4, 3/4)^T$, ${\bf w}_3=(1/3, 2/3)^T$和${\bf w}_4=(1/2, 1/2)^T$或者${\bf w}_1=(1/2001, 2000/2001)^T$, ${\bf w}_2=(1/2000, 1999/2000)^T$, $\cdots$, ${\bf w}_{2000}=(1/2, 1/2)^T$,对应的渐近比值被计算并且列在表 1或者图 2.显然,所有的渐近比值都比$1$小.这些数值结果证实了投资组合损失${\bf w}^T{\bf X}$渐近随机地小于对应的投资组合损失${\bf w}^T{\bf Y}$,其中${\bf w}\in \Sigma_2$.上述观测结果是显然的,因为对于$\rho_1< \rho_2$,渐近比值$\left(\frac{w_1^2+w_2^2+2\rho_1w_1w_2}{w_1^2+w_2^2 +2\rho_2w_1w_2}\right)^{\alpha/2}\le 1$.