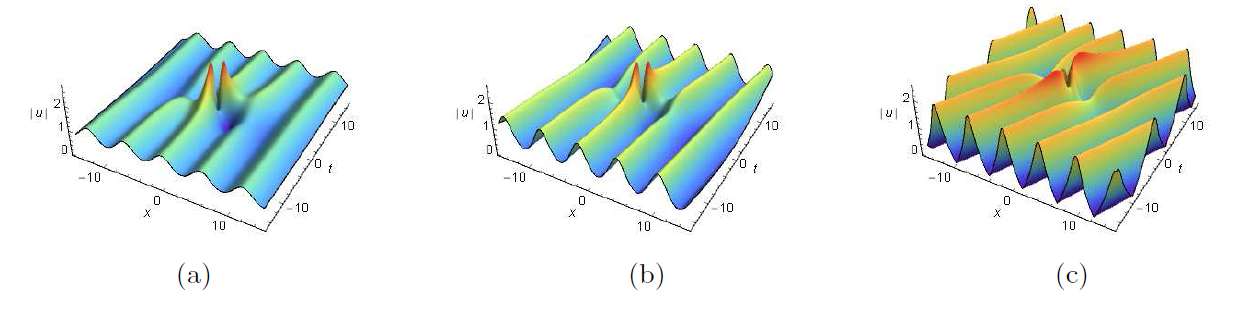
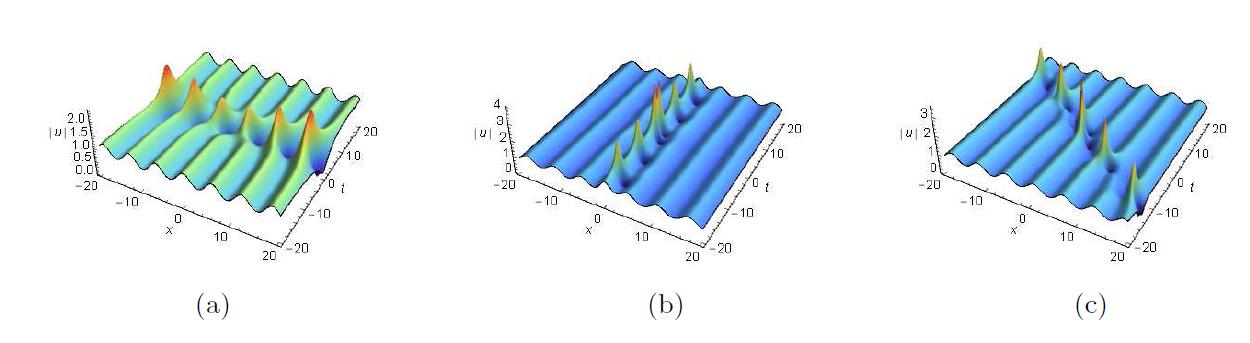
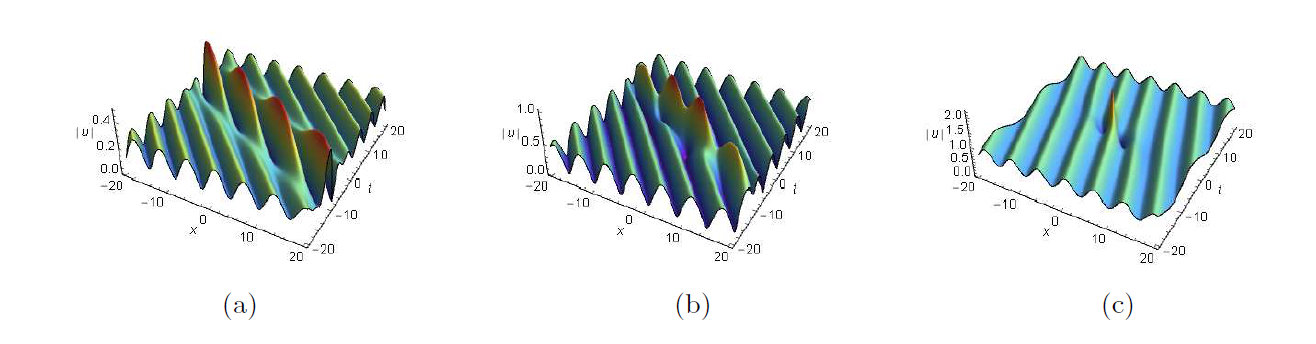
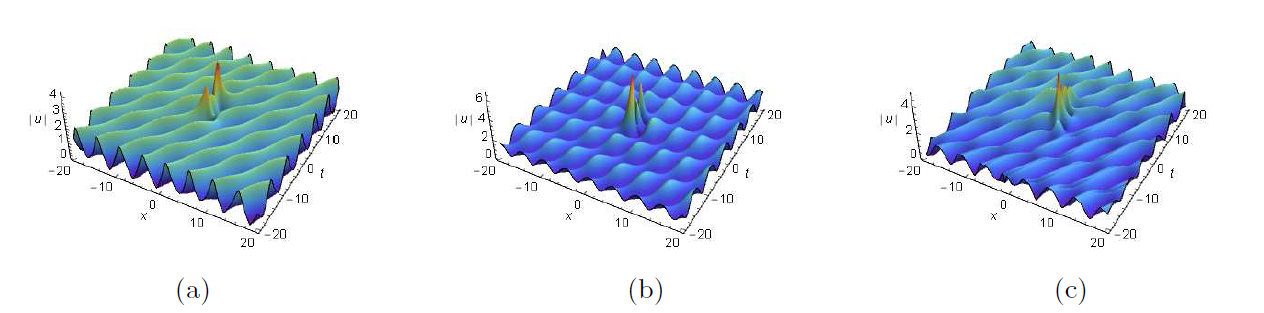
Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (6): 1511-1519.
Previous Articles Next Articles
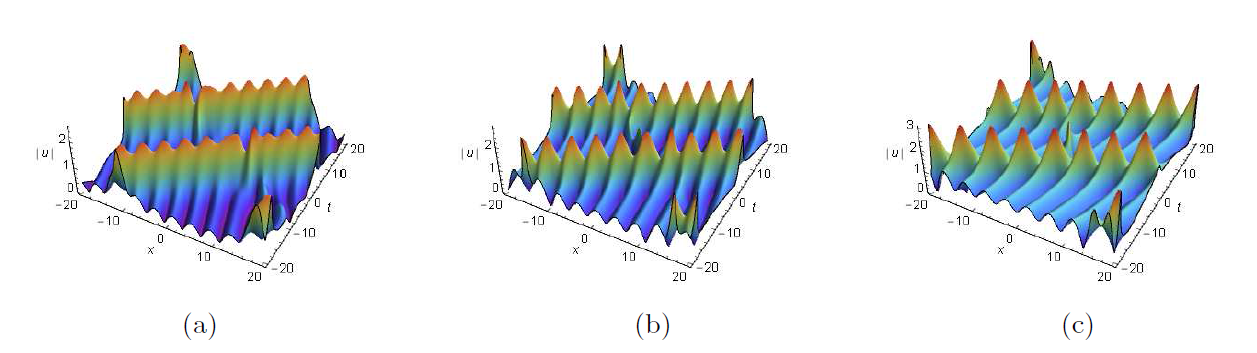
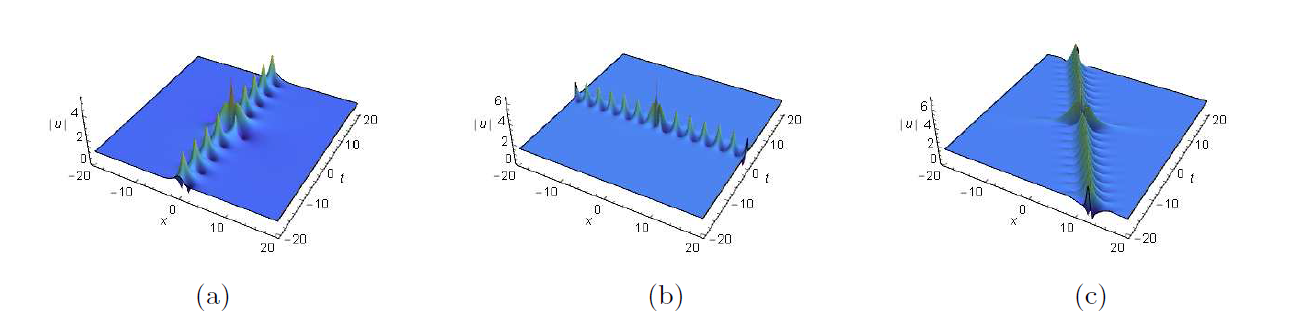
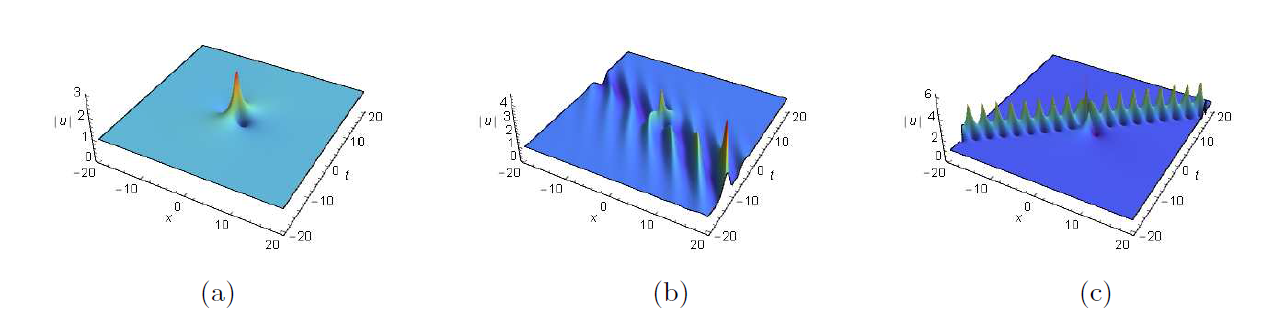
Breather and Rogue Wave on the Periodic/Double Periodic Background and Interaction Solutions of the Generalized Derivative Nonlinear Schr



- 1Public Basic Education Department, Zhejiang Industry Polytechnic College, Zhejiang Shaoxing 312000
2Department of Mathematics, Zhejiang Normal University, Zhejiang Jinhua 321004
-
Received:2023-11-30Revised:2024-04-28Online:2024-12-26Published:2024-11-22 -
Supported by:NSFC(11371326);NSFC(11975145);NSFC(12271488)
CLC Number:
- 0175.24
Cite this article
Lou Yu, Zhang Yi. Breather and Rogue Wave on the Periodic/Double Periodic Background and Interaction Solutions of the Generalized Derivative Nonlinear Schr

share this article
| [1] | Olver P J, Sattinger D H. Solitons in Physics, Mathematics, and Nonlinear Optics. New York: Springer, 1990 |
| [2] | Burger S, Bongs K, Dettmer S, Ertmer W, Sengstock K. Dark solitons in Bose-Einstein condenstates. Phys Rev Lett, 1999, 83: 5198-5201 |
| [3] | Bludov Y V, Konotop V V, Akhmediev N. Matter rogue waves. Phys Rev A, 2009, 80: 033610 |
| [4] |
Yang B, Chen Y. Dynamics of high-order solitons in the nonlocal nonlinear Schr  |
| [5] | Ma W X. Riemann-Hilbert problems of a six-component mKdV system and its soliton solutions. Acta Math Sci, 2019, 29(2): 509-523 |
| [6] |
Akhmediev N, Korbeev V I. Modulation instability and periodic soulutions of the nonlinear Schr  |
| [7] | Kuznetsov E A. Solitons in a parametrically unstable plasma. Dokl Akad Nauk SSSR, 1977, 236: 575-577 |
| [8] | Priya N V, Senthilvelan M, Lakshmanan M. Akhmediev breathers, Ma solitons and general breathers from rogue waves: A case study in the Manakov system. Phys Rev E, 2013, 88(2): 022918 |
| [9] | Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett A, 2009, 373: 675-678 |
| [10] | Wu X H, Gao Y T, Yu X, et al. Binary Darboux transformation, solitons, periodic waves and modulation instability for a nonlocal Lakshmana-Porsezian-Daniel equation. Wave Motion, 2022, 114: 103036 |
| [11] |
Zhai Y Y, Ji T, Geng X G. Coupled derivative nonlinear Schr  |
| [12] |
L  |
| [13] | 房春梅, 田守富. 约化的(3+1)维 Hirota 方程的呼吸波解、Lump 解和半有理解. 数学物理学报, 2022, 42A(3): 775-783 |
| Fang C M, Tian S F. Breather Wave Solutions, Lump solutions and semi-rational solutions of a reduced (3+1) dimensional Hirota equation. Acta Math Sci, 2022, 42A(3): 775-783 | |
| [14] | Ma W X. Bilinear equations and resonant solutions characterized by Bell polynomials. Rep Math Phys, 2013, 72(1): 41-56 |
| [15] | Ma W X. Trilinear equations, Bell polynomials, and resonant solutions. Front Math China, 2013, 8: 1139-1156 |
| [16] |
田守富. 一个广义导数非线性 Schr  |
Tian S F. Riemann-Hilbert problem to a generalized derivative nonlinear Schr  |
|
| [17] |
Wei H Y, Fan E G, Guo H D. Riemann-Hilbert approach and nonlinear dynamics of the coupled higher-order nonlinear Schr  |
| [18] | Chen X T, Zhang Y, Ye R S. Riemann-Hilbert approach of the coupled nonisospectral Gross-Pitaevskii system and its multi-component generalization. Appl Anal, 2019, 100(10): 2200-2209 |
| [19] | Hu B B, Xia T C, Ma W X. Riemann-Hilbert approach for an initial-boundary value problem of the two-component modified Korteweg-de Vries equation on the half-line. Appl Math Comput, 2018, 332: 148-159 |
| [20] |
Guo B L, Ling L M, Liu Q P, Wu C F. Nonlinear Schr  |
| [21] |
Wang X, Wei J. Three types of Darboux transformation and general soliton soulutions for the space-shifted nonlocal PT symmetric nonlinear Schr  |
| [22] | Zhang Y, Ye R S, Ma W X. Binary Darboux transformation and soliton solutions for the coupled complex modified Korteweg-de Vries equations. Math Meth Appl Sci, 2019, 43: 613-627 |
| [23] |
Fan E G. Integrable evolution systems based on Gerdjikov-Ivanovequations, bi-Hamiltonian structure, finite-dimensional integrable systems and  |
| [24] |
Shen Y, Tian B, Zhou T Y, Gao X T.  |
| [25] | Kodama Y J. Optical solitons in a monomode fiber. J Stat Phys, 1985, 39: 597 |
| [26] | Chen J B, Pelinovsky D E, Upsal J. Modulation instability of periodic standing waves in the derivative NLS equation. J Nonlinear Sci, 2021, 31: 58 |
| [27] |
Zhang N, Xia T C, Fan E G. A Riemann-Hilbert approach to the Chen-Lee-Liu equation on the half line. Acta Math Appl Sin-E, 2018, 34: 493-515
doi: 10.1007/s10255-018-0765-7 |
| [28] | Xu S W, He J S. The rogue wave and breather solution of the Gerdjikov-Ivanov equation. J Math Phys, 2012, 53: 063507 |
| [29] |
Li X Y, Han G F, Zhao Q L. Interactions of localized wave and dynamics analysis in generalized derivative nonlinear Schr  |
| [1] |
Qian Yuting, Zhou Xueliang, Cheng Zhibo.
Existence of Periodic Solutions for  |
| [2] |
Qian Yuting, Zhou Xueliang, Cheng Zhibo.
Existence of Periodic Solutions for  |
| [3] | Yin Ruixia, Wang Zedong, Zhang Long. A Periodic Stage Structure Single-Population Model with Infinite Delay and Feedback Control [J]. Acta mathematica scientia,Series A, 2024, 44(4): 994-1011. |
| [4] | Yang Jiaopeng, Liang Yong. Solitary and Periodic Solutions of the Generalized b-equation [J]. Acta mathematica scientia,Series A, 2024, 44(3): 670-686. |
| [5] | Wang Zihuan,Wang Chao. Symmetric and Periodic Solutions for a Class of Weakly Coupled Systems Composed of Two Particles with Obstacles [J]. Acta mathematica scientia,Series A, 2023, 43(5): 1427-1439. |
| [6] | Shan Yuan. Relative Morse Index and Multiple Solutions for Asymptotically Linear Dirac Equation [J]. Acta mathematica scientia,Series A, 2023, 43(1): 69-81. |
| [7] | Tang Yuxuan, Zhou Guoquan. The Rogue Wave Solution of MNLS Equation Based on Hirota's Bi-linear Derivative Transformation [J]. Acta mathematica scientia,Series A, 2023, 43(1): 132-142. |
| [8] | Song Huijuan, Huang Qian, Wang Zejia. Asymptotic Analysis of a Tumor Model with Angiogenesis and a Periodic Supply of External Nutrients [J]. Acta mathematica scientia,Series A, 2023, 43(1): 261-273. |
| [9] | Jiayu Liu,Hanyu Wei,Yan Zhang,Tiecheng Xia,Hui Wang. Soliton Solutions and Its Nonlinear Dynamics Behavior Research of the Three-Component Four-Order Nonlinear Schrödinger System in Alpha Helical Protein [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1873-1885. |
| [10] | Xuelei Wang. Large Multiple Periodic Solutions for the 1-Dimensional Sub-Linear p-Laplacian Equation [J]. Acta mathematica scientia,Series A, 2022, 42(5): 1462-1472. |
| [11] | Nan Deng,Meiqiang Feng. Positive Doubly Periodic Solutions To Telegraph Equations: Existence, Uniqueness, Multiplicity and Asymptotic Behavior [J]. Acta mathematica scientia,Series A, 2022, 42(5): 1360-1380. |
| [12] | Chunmei Fang,Shoufu Tian. Breather Wave Solutions, Lump Solutions and Semi-Rational Solutions of a Reduced (3+1)Dimensional Hirota Equation [J]. Acta mathematica scientia,Series A, 2022, 42(3): 775-783. |
| [13] | Shaowen Yao,Wenjie Li,Zhibo Cheng. Nondegeneracy and Uniqueness of Periodic Solution for Third-Order Nonlinear Differential Equations [J]. Acta mathematica scientia,Series A, 2022, 42(2): 454-462. |
| [14] | Jun Lan. Existence and Multiplicity of Anti-Periodic Solutions for a Class of Second Order Duffing Equation [J]. Acta mathematica scientia,Series A, 2022, 42(2): 463-469. |
| [15] | Chenyang Xia,Zhenhui Wang,Zhibo Cheng. Positive Periodic Solutions for a Damped Duffing Equation with Singularity of Attractive Type [J]. Acta mathematica scientia,Series A, 2022, 42(1): 131-138. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 284
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 72
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|