Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (6): 1520-1536.
Previous Articles Next Articles
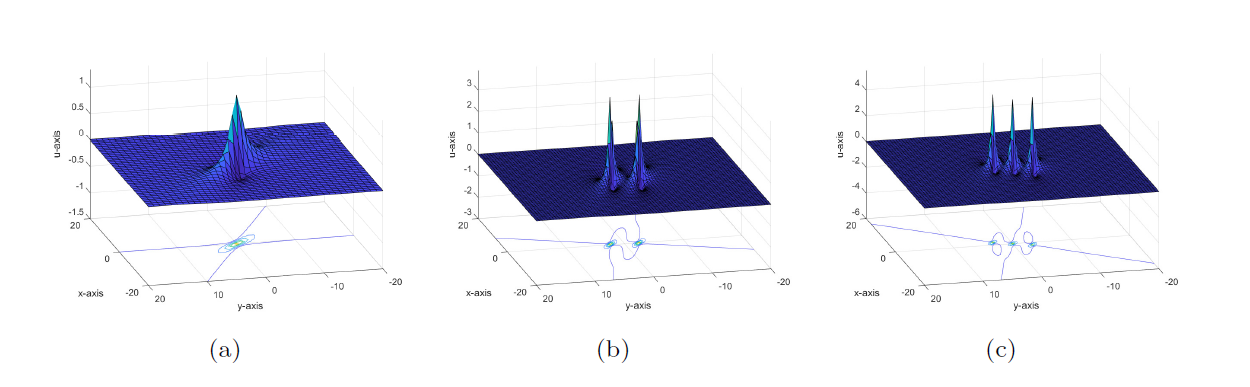
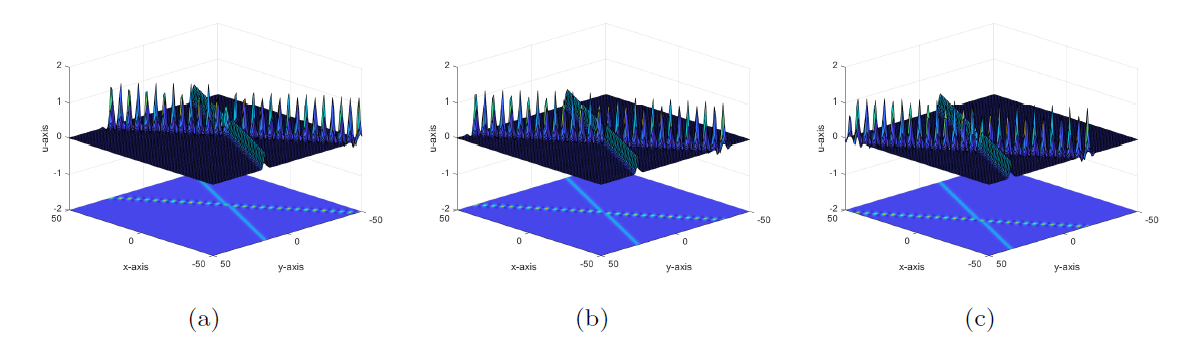
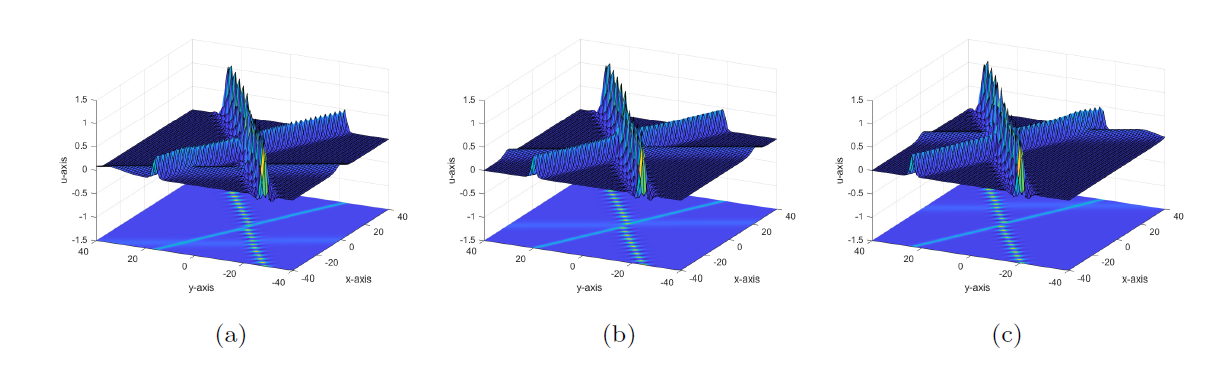
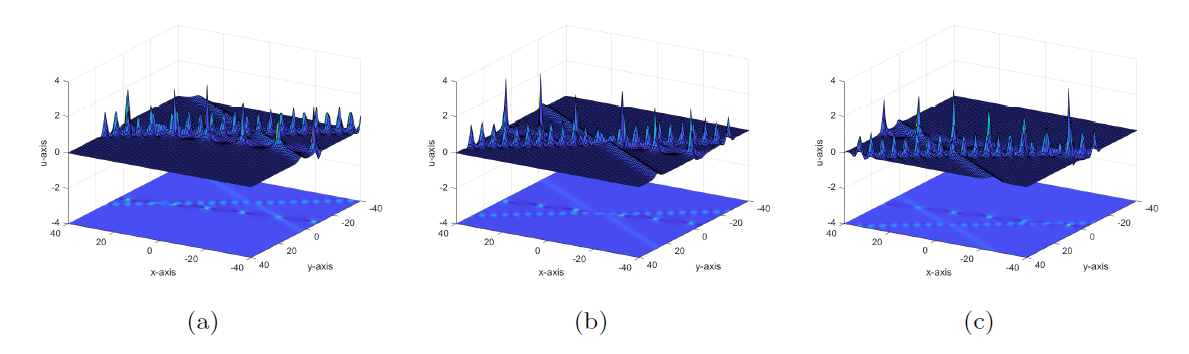
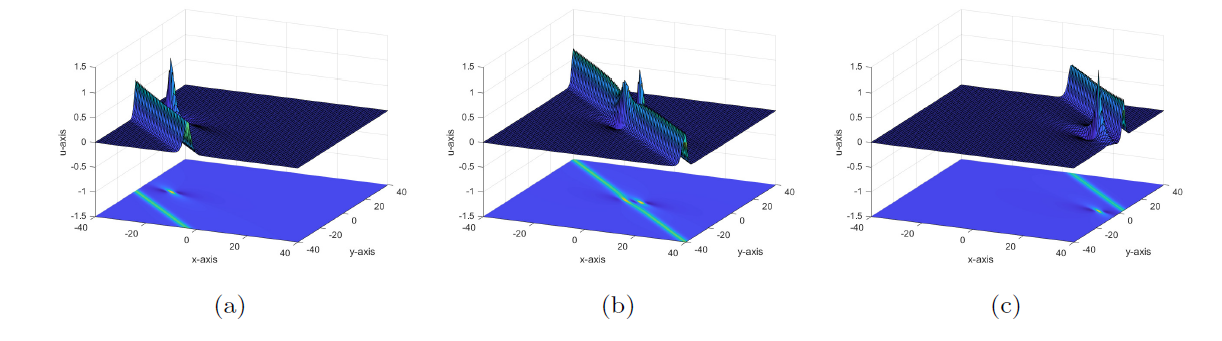
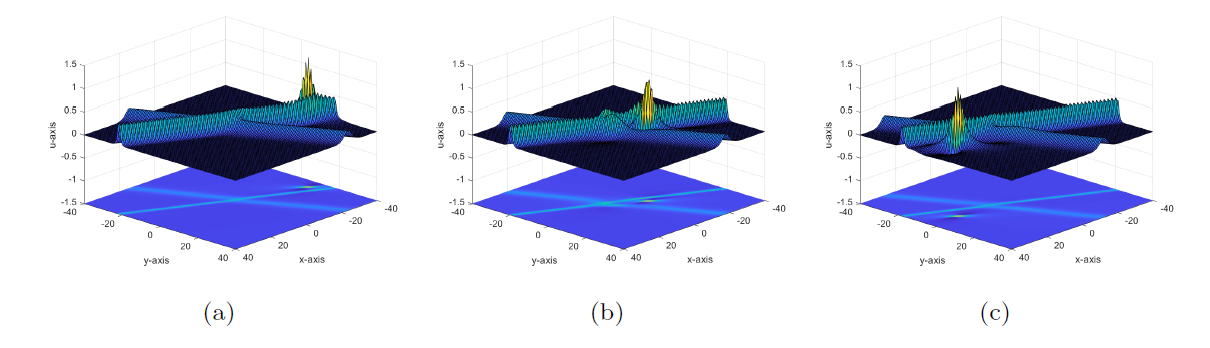
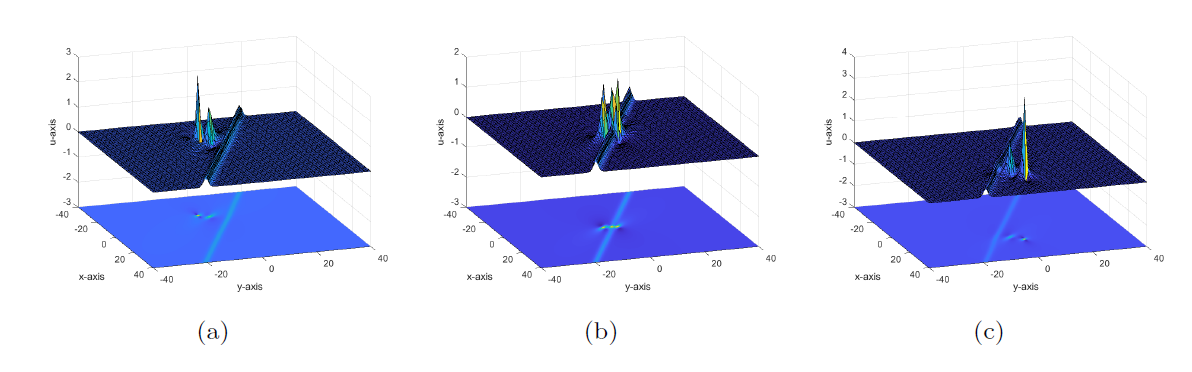
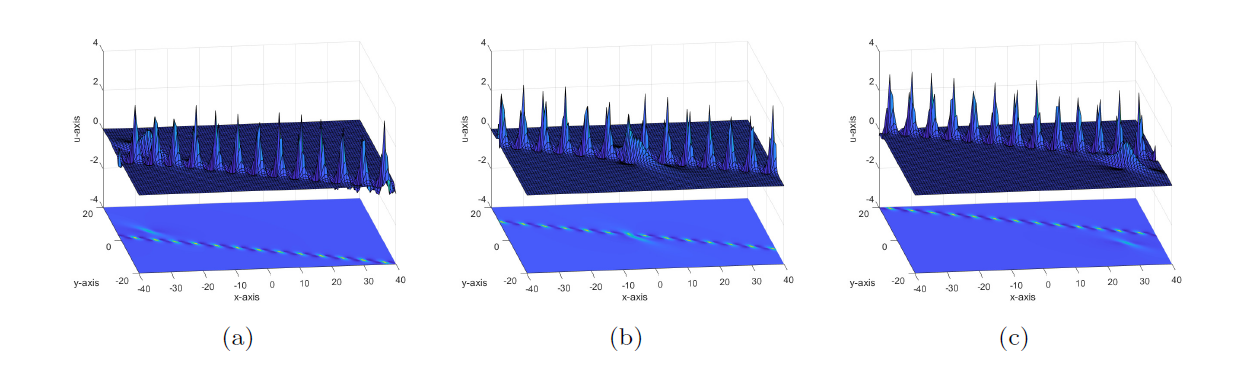
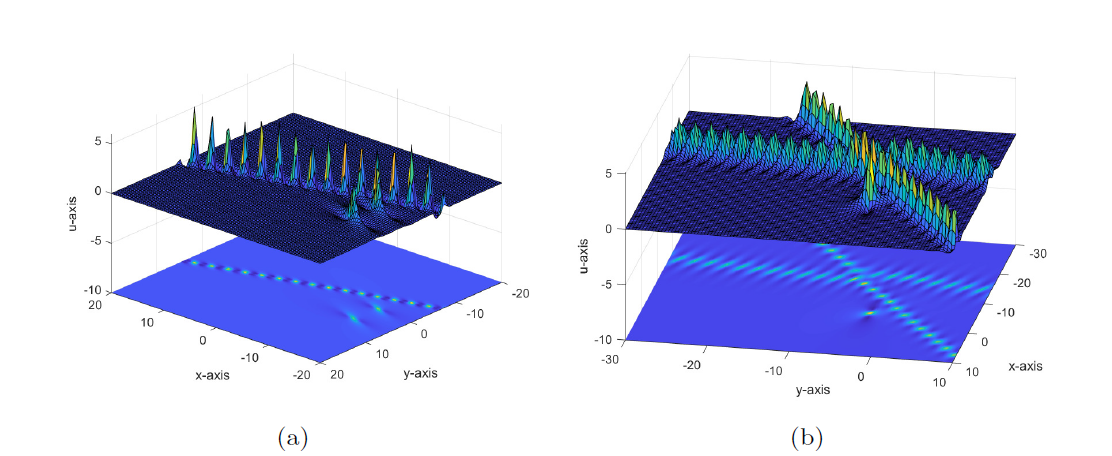
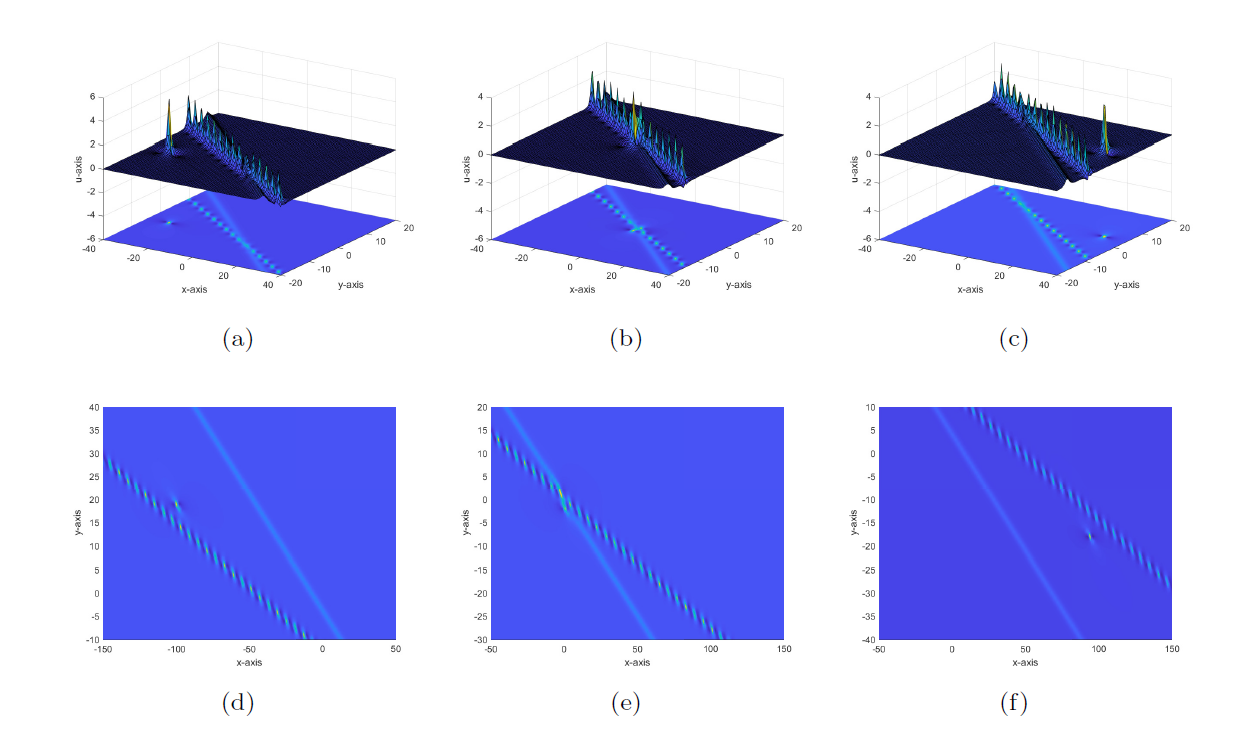
Degeneration Behaviors of Solutions and Hybrid Solutions for the New (3+1)-Dimensional KP Equation
Guo Yanfeng1,*( ),Cui Jingyi1(
),Cui Jingyi1( ),Xiao Haijun1(
),Xiao Haijun1( ),Zhang Jingjun2(
),Zhang Jingjun2( )
)
- 1School of Mathematics and Physics, China University of Geosciences, Wuhan 430074
2College of Data Science, Jiaxing University, Zhejiang Jiaxing 314001
-
Received:2024-01-30Revised:2024-04-29Online:2024-12-26Published:2024-11-22 -
Supported by:NSFC(11861013);NSFC(11771183);NSFC(12261053);Guangxi Science and Technology Base and Talent Special Project(AD21238019)
CLC Number:
- 0175.29
Cite this article
Guo Yanfeng, Cui Jingyi, Xiao Haijun, Zhang Jingjun. Degeneration Behaviors of Solutions and Hybrid Solutions for the New (3+1)-Dimensional KP Equation[J].Acta mathematica scientia,Series A, 2024, 44(6): 1520-1536.
share this article
| [1] | Hirota R. Exact solution of the Korteweg-de vries equation for multiple collisions of solitons. Phys Rev Lett, 1971, 27(18): 1192-1194 |
| [2] | Staruszkiewicz A. A nonlinear modification of the Schrödinger equation. Acta Phys Pol B, 1983, 14(12): 907-909 |
| [3] | Wazwaz A M. Painlevé analysis for new (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equations with constant and time-dependent coefficients. Int J Numer Methods Heat Fluid Flow, 2020, 30(9): 4259-4266 |
| [4] | Zhao Z H, Dai Z D, Wang C J. Extend three-wave method for the (1+2)-dimensional Ito equation. Appl Math Comput, 2010, 217(5): 2295-2300 |
| [5] | Wazwaz A M. Integrable (3+1)-dimensional Ito equation: variety of lump solutions and multiple-soliton solutions. Nonlinear Dyn, 2022, 109(3): 1929-1934 |
| [6] | Ma W X. Lump solutions to the Kadomtsev-Petviashvili equation. Phys Lett A, 2015, 379(36): 1975-1978 |
| [7] | Chen S J, Lü X. Lump and lump-multi-kink solutions in the (3+1)-dimensions. Commun Nonlinear Sci Numer Simul, 2022, 109: 106103 |
| [8] | Seadawy A R, Ahmed S, Rizvi S T, Ali K. Various forms of lumps and interaction solutions to generalized Vakhnenko Parkes equation arising from high-frequency wave propagation in electromagnetic physics. J Geom Phys, 2022, 176: 104507 |
| [9] | Tan W, Dai Z D, Yin Z Y. Dynamics of multi-breathers, N-solitons and M-lump solutions in the (2+1)-dimensional KdV equation. Nonlinear Dyn, 2019, 96(2): 1605-1614 |
| [10] | Wang H, Wang Y. Breather waves, rogue waves and complexiton solutions for a Zakharov-Kuznetsov equation. J Geom Phys, 2021, 167: 104286 |
| [11] | Li L X. Degeneration of solitons for a (3+1)-dimensional generalized nonlinear evolution equation for shallow water waves. Nonlinear Dyn, 2022, 108(2): 1627-1640 |
| [12] | Zhao Z L, He L C. M-lump,high-order breather solutions and interaction dynamics of a generalized (2+1)-dimensional nonlinear wave equation. Nonlinear Dyn, 2020, 100(3): 2753-2765 |
| [13] | Li L X, Dai Z D, Cheng B T. Degeneration of N-soliton solutions for a (3+1)-dimensional nonlinear model in shallow water waves. Nonlinear Dyn, 2023, 111(2): 1667-1683 |
| [14] | Zhou X, Ilhan O A, Manafian J, et al. N-lump and interaction solutions of localized waves to the (2+1)-dimensional generalized KDKK equation. J Geom Phys, 2021, 168: 104312 |
| [15] | Hirota R. Exact envelope-soliton solutions of a nonlinear wave equation. J Math Phys, 1973, 14(7): 805-809 |
| [16] | Cui J Y, Li D L, Zhang T F. Symmetry reduction and exact solutions of the (3+1)-dimensional nKdV-nCBS equation. Appl Math Lett, 2023, 144: 108718 |
| [17] | Ma W X. N-soliton solutions and the Hirota conditions in (2+1)-dimensions. Opt Quant Electron, 2020, 52(12): Article 511 |
| [18] | Zhao X, Tian B, Du X X, et al. Bilinear Bäcklund transformation, kink and breather-wave solutions for a generalized (2+1)-dimensional Hirota-Satsuma-Ito equation in fluid mechanics. Eur Phys J Plus, 2021, 136(2): 1-9 |
| [19] | Chen X, Guo Y F, Zhang T F. Some new kink type solutions for the new (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation. Nonlinear Dyn, 2023, 111(1): 683-695 |
| [20] | Sulaiman T A, Yusuf A, Abdeljabbar A, Alquran M. Dynamics of lump collision phenomena to the (3+1)-dimensional nonlinear evolution equation. J Geom Phys, 2021, 169: 104347 |
| [21] | Guo Y F, Dai Z D, Guo C X. Lump solutions and interaction solutions for (2+1)-dimensional KPI equation. Front Math China, 2022, 17(5): 875-886 |
| [22] | Ma H C, Chen Q X, Deng A P. Soliton molecules and some novel hybrid solutions for the (2+1)-dimensional generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt equation. Commun Theor Phys, 2020, 72(9): 095001 |
| [23] | Zhang W J, Xia T C. Solitary wave, M-lump and localized interaction solutions to the (4+1)-dimensional Fokas equation. Phys Scr, 2020, 95(4): 045217 |
| [24] | Wazwaz A M, Alatawi N S, Albalawi W, El-Tantawy S A. Painlevé analysis for a new (3+1)-dimensional KP equation: Multiple-soliton and lump solutions. Euro Phys Lett, 2022, 140(5): 52002 |
| [25] | Ahmad S, Khan S A, Hadi F. Damped Kadomtsev-Petviashvili equation for weakly dissipative solitons in dense relativistic degenerate plasmas. Commun Theor Phys, 2017, 68(6): 783 |
| [26] | Fogaca D A, Navarra F S, Ferreira Filho L G. Kadomtsev-Petviashvili equation in relativistic fluid dynamics. Commun Nonlinear Sci Numer Simul, 2013, 18(2): 221-235 |
| [27] | Ma W X, Batwa S, Manukure S. Dispersion-managed lump waves in a spatial symmetric KP model. E Asian J Appl Math, 2023, 13(2): 246-256 |
| [28] | Ma W X. Lump waves in a spatial symmetric nonlinear dispersive wave model in (2+1)-dimensions. Mathematics, 2023, 11(22): 4664 |
| [29] | Wang H. Lump and interaction solutions to the (2+1)-dimensional Burgers equation. Appl Math Lett, 2018, 85: 27-34 |
| [30] | Ma W X. A novel kind of reduced integrable matrix mKdV equations and their binary Darboux transformations. Mod Phys Lett B, 2022, 36(20): 2250094 |
| [31] | Ma W X. Linear superposition of Wronskian rational solutions to the KdV equation. Commun Theor Phys, 2021, 73(6): 065001 |
| [32] | Ma W X. Four-component integrable hierarchies of Hamiltonian equations with (m+n+2)th-order Lax pairs. Theor Math Phys, 2023, 216(2): 1180-1188 |
| [33] | Ma W X. Novel Liouville integrable Hamiltonian models with six components and three signs. Chin J Phys, 2023, 86: 292-299 |
| No related articles found! |
|