带间断系数的奇异摄动对流扩散方程的 NIPG 有限元方法

Abstract

Abstract:

In this paper, a higher order NIPG method on a Bakhvalov-type mesh for a singularly perturbed convection-diffusion problem with a discontinuous convection coefficient is studied. Based on Gauß Radau interpolation and Lagrange interpolation, the convergence of optimal order in an energy norm is derived. Numerical experiments are proposed to confirm our theoretical results.

Key words: Singularly perturbed, Nonsmooth coefficient, NIPG method, Bakhvalov-type mesh

CLC Number:

0175.23

Xu Lei, Liu Libin. Uniformly Convergent NIPG Methods for a Singularly Perturbed Convection-Diffusion Problem with a Discontinuous Convection Coefficient[J].Acta mathematica scientia,Series A, 2024, 44(6): 1499-1510.

Trendmd

Figures/Tables 6

References 16

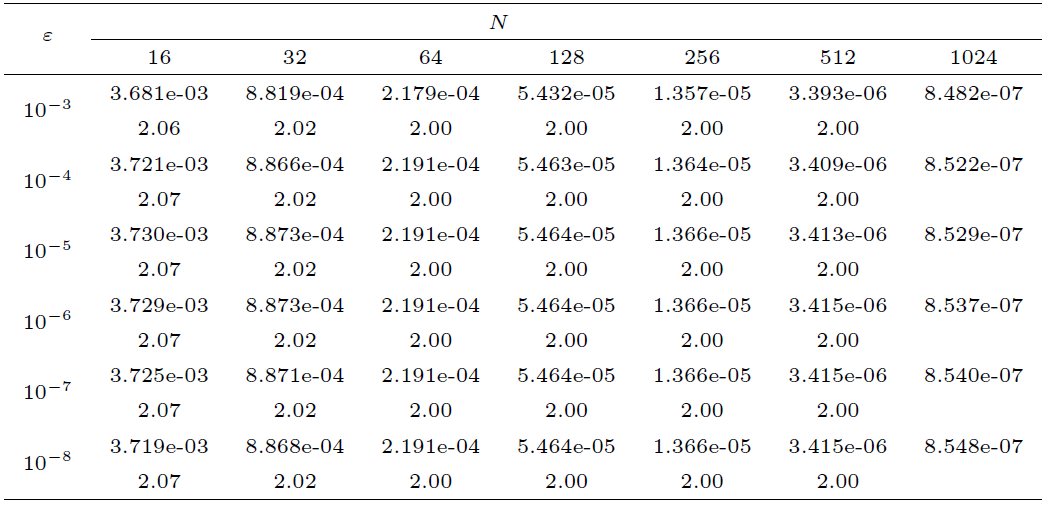
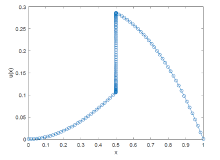
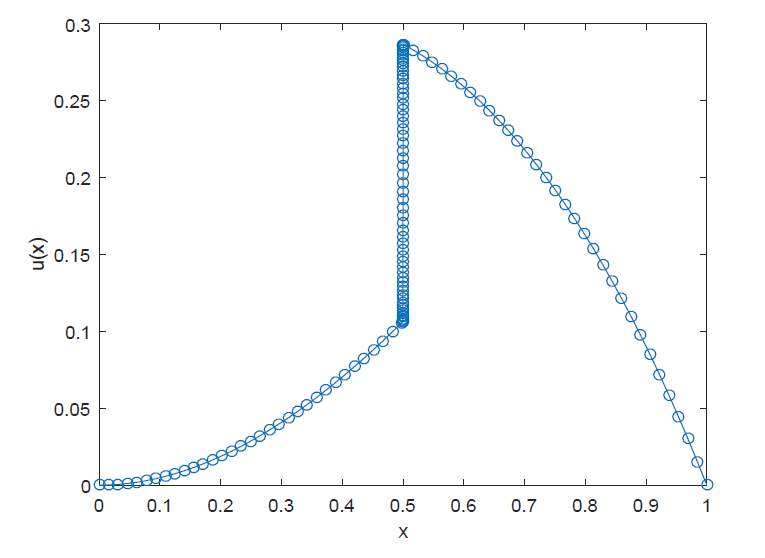
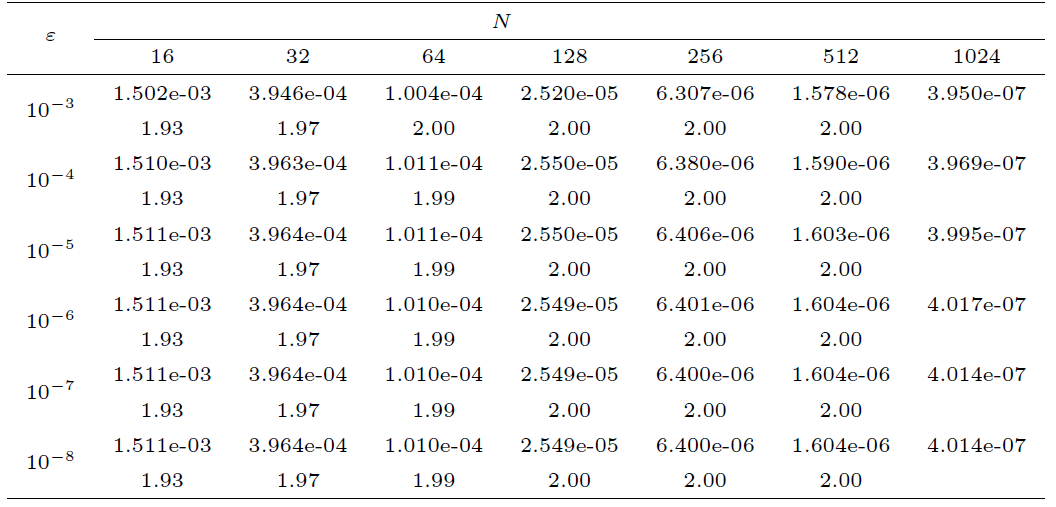
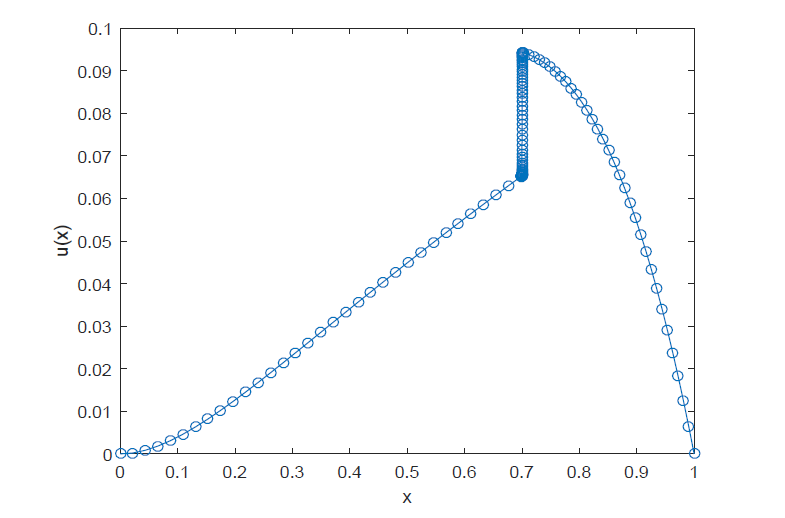
[1]	Zhang J, Ma X Q, Lv Y H. Finite element method on Shishkin mesh for a singularly perturbed problem with an interior layer. Applied Mathematics Letters, 2021, 121: 107509
[2]	Roos H G, Stynes M, Tobiska L. Numerical Methods for Singularly Perturbed Differential Equation. Berlin: Springer, 2008
[3]	Prabha T, Chandru M, Shanthi V. Hybrid difference scheme for singularly perturbed reaction-convection-diffusion problem with boundary and interior layers. Applied Mathematics and Computation, 2017, 314: 237-256
[4]	Chandru M, Prabha T, Shanthi V. A parameter robust higher order numerical method for singularly perturbed two parameter problems with non-smooth data. Journal of Computational and Applied Mathematics, 2017, 309: 11-27
[5]	Zarin H, Gordic S. Numerical solving of singularly perturbed boundary value problems with discontinuities. Novi Sad Journal of Mathematics, 2012, 42(1): 131-145
[6]	Babu A R, Ramanujam N. The SDFEM for singularly perturbed convection-diffusion problems with discontinuous source term arising in the chemical reactor theory. International Journal of Computer Mathematics, 2011, 88(8): 1664-1680
[7]	Linß T, Stynes M. Numerical methods on Shishkin meshes for linear convection-diffusion problems. Computer Methods in Applied Mechanics and Engineering, 2001, 190(28): 3527-3542
[8]	Zarin H, Roos H G. Interior penalty discontinuous approximations of convection-diffusion problems with parabolic layers. Numerische Mathematik, 2005, 100(4): 735-759
[9]	Zarin H. On discontinuous Galerkin finite element method for singularly perturbed delay differential equations. Applied Mathematics Letters, 2014, 38: 27-32
[10]	Roos H G, Zarin H. A supercloseness result for the discontinuous Galerkin stabilization of convection-diffusion problems on Shishkin meshes. Numerical Methods for Partial Differential Equations, 2007, 23(6): 1560-1576
[11]	Zhu P, Yang Y B, Yin Y H. Higher order uniformly convergent NIPG methods for 1-d singularly perturbed problems of convection-diffusion type. Applied Mathematical Modelling, 2015, 39(22): 6806-6816
[12]	Zhang J, Liu X W. Optimal order of uniform convergence for finite element method on Bakhvalov-type meshes. Journal of Scientific Computing, 2020, 85(1): Article 2
[13]	Cheng Y. On the local discontinuous Galerkin method for singularly perturbed problem with two parameters. Journal of Computational and Applied Mathematics, 2021, 392(22): 113485
[14]	Ciarlet P G. The Finite Element Method for Elliptic Problems. Philadelphia: SIAM, 2002
[15]	Ma X Q, Zhang J. Supercloseness analysis of the nonsymmetric interior penalty Galerkin method for a singularly perturbed problem on Bakhvalov-type mesh. Applied Mathematics Letters, 2023, 144: 108701
[16]	Zhu P, Xie Z Q, Zhou S Z. A coupled continuous-discontinuous FEM approach for convection diffusion equations. Acta Math Sci, 2011, 31B(2): 601-612

Uniformly Convergent NIPG Methods for a Singularly Perturbed Convection-Diffusion Problem with a Discontinuous Convection Coefficient

RichHTML

PDF (PC)

Abstract

Cite this article

share this article

Figures/Tables 6

References 16

Related Articles 4

Metrics

Comments

Recommended 10

[1]	Fu Yuechen, Ni Mingkang. The Inner Layer of a Class of Singularly Perturbed High-Order Equations with Discontinuous Right-Hand Side [J]. Acta mathematica scientia,Series A, 2024, 44(5): 1153-1166.
[2]	YANG Yu-Bo, ZHU Peng, YIN Yun-Hui. A Optimal Uniformly Convergent Discontinuous Galerkin Finite Element Method for Singularly Perturbed Problem [J]. Acta mathematica scientia,Series A, 2014, 34(3): 716-726.
[3]	ZHONG Min-Ling, ZHANG Xin-Guang. Positive Solutions of Singularly Perturbed (k, n-k) Conjugate Boundary Value Problems [J]. Acta mathematica scientia,Series A, 2011, 31(1): 263-272.
[4]	Wang Aifeng;Ni Mingkang. The Spike-type Contrast Structures for a Nonlinear Singularly Perturbed Second Order Equation [J]. Acta mathematica scientia,Series A, 2009, 29(1): 208-216.