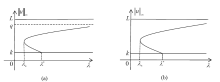
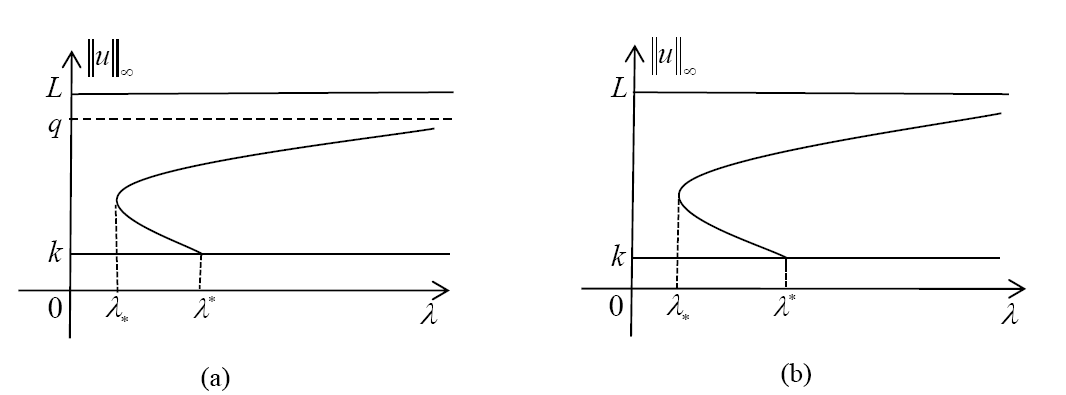
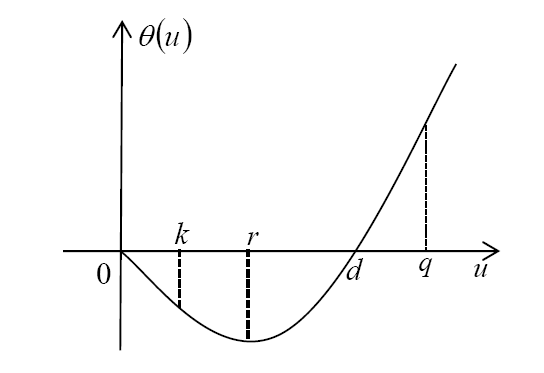
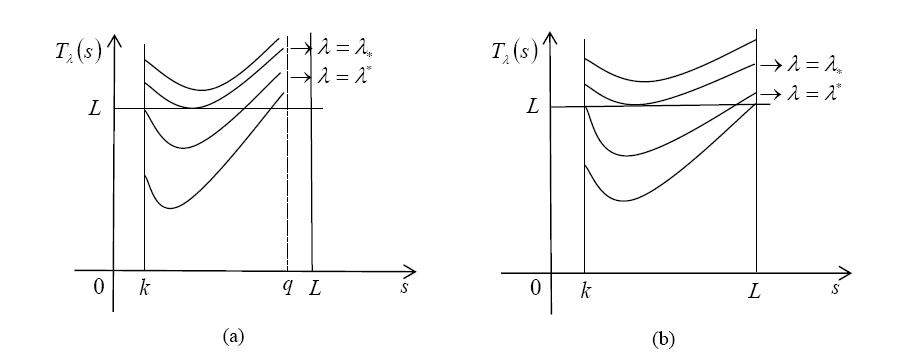
Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (5): 1341-1349.
Previous Articles Next Articles
Exact Multiplicity of Positive Solutions for a Semipositone Mean Curvature Problem with Concave Nonlinearity
Li Xiaodong*( ),Gao Hongliang(
),Gao Hongliang( ),Xu Jing
),Xu Jing
- Department of Mathematics, Lanzhou Jiaotong University, Lanzhou 730070
-
Received:2022-10-09Revised:2023-04-10Online:2023-10-26Published:2023-08-09 -
Contact:Xiaodong Li E-mail:LXD5775@163.com;gaohongliang101@163.com -
Supported by:NSFC(11801243);NSFC(11961039);Gansu Province Colleges and Universities Young Doctor fund project(2022QB-056);Young Scholars Science Foundation of Lanzhou Jiaotong University(2017012)
CLC Number:
- O175.8
Cite this article
Li Xiaodong, Gao Hongliang, Xu Jing. Exact Multiplicity of Positive Solutions for a Semipositone Mean Curvature Problem with Concave Nonlinearity[J].Acta mathematica scientia,Series A, 2023, 43(5): 1341-1349.
share this article
| [1] | Bratu G. Sur les equation integrals non linéarires. Bull Soc Math France, 1914, 42: 113-142 |
| [2] | Corsato C. Mathematical Analysis of Some Differential Models Involving the Euclidean or the Minkowski Mean Curvature Operator. Trieste: University of Trieste, 2015 |
| [3] | Gao H L, Xu J. Bifurcation curves and exact multiplicity of positive solutions for Dirichlet problems with the Minkowski-curvature equation. Boundary Value Problems, 2021, Article number 81 |
| [4] | Gelfand I M. Some problems in the theory of quasilinear equations. American Mathematical Society Translations, 1963, 29(2): 295-381 |
| [5] |
Huang S Y. Global bifurcation diagrams for Liouville-Bratu-Gelfand problem with Minkowski-curvature operator. Journal of Dynamics and Differential Equations, 2021, 34: 2157-2172
doi: 10.1007/s10884-021-09982-4 |
| [6] |
Huang S Y. Exact multiplicity and bifurcation curves of positive solutions of a one-dimensional Minkowski-curvature problem and its application. Communications on Pure and Applied Analysis, 2018, 17(3): 1271-1294
doi: 10.3934/cpaa.2018061 |
| [7] |
Huang S Y. Classifification and evolution of bifurcation curves for the one-dimensional Minkowski-curvature problem and its applications. Journal of Differential Equations, 2018, 264(9): 5977-6011
doi: 10.1016/j.jde.2018.01.021 |
| [8] |
Huang S Y. Global bifurcation and exact multiplicity of positive solutions for the one-dimensional Minkowski-curvature problem with sign-changing nonlinearity. Communications on Pure and Applied Analysis, 2019, 18(6): 3267-3284
doi: 10.3934/cpaa.2019147 |
| [9] | Huang S Y. Bifurcation diagrams of positive solutions for one-dimensional Minkowski-curvature problem and its applications. Discrete and Continuous Dynamical Systems-A, 2019, 39(6): 3443-3462 |
| [10] | Huang S Y, Hwang M S. Bifurcation curves of positive solutions for the Minkowski-curvature problem with cubic nonlinearity. Electronic Journal of Qualitative Theory of Differential Equations, 2021, Article number 41 |
| [11] | Hutten E H. Relativistic (non-linear) Oscillator. Nature, 1965, 205(4974): 892 |
| [12] | Walter G. Classicai Mechanics-point Particles and Relativity. New York: Springer, 2004: 1-485 |
| [13] | Zhang X M, Feng M Q. Bifurcation diagrams and exact multiplicity of positive solutions of one-dimensional prescribed mean curvature equation in Minkowski space. Communications in Contemporary Mathematics, 2019, 21(3): 111-137 |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 378
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 97
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|