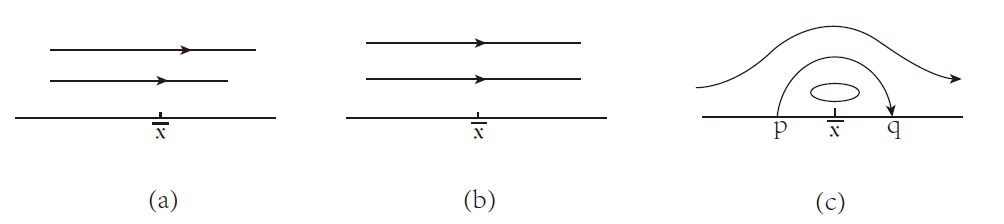Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (4): 1123-1132.
Previous Articles Next Articles
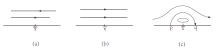
Boundary Layer Separation of 2-D Incompressible Navier-Stokes-Allen-Cahn System
Chen Min( ),Hu Biyan(
),Hu Biyan( ),Luo Hong*(
),Luo Hong*( )
)
- School of Mathematics Science, Sichuan Normal University, Chengdu 610068
-
Received:2022-07-17Revised:2023-02-11Online:2023-08-26Published:2023-07-03 -
Contact:Hong Luo E-mail:1653637845@qq.com;2838954298@qq.com;lhscnu@163.com -
Supported by:NSFC(12171343);Scientific Research Fund of the Science and Technology Department of Sichuan Province(22CXTD0029)
CLC Number:
- O175.29
Cite this article
Chen Min,Hu Biyan,Luo Hong. Boundary Layer Separation of 2-D Incompressible Navier-Stokes-Allen-Cahn System[J].Acta mathematica scientia,Series A, 2023, 43(4): 1123-1132.
share this article
| [1] |
Xu X, Zhao L Y, Liu C. Axisymmetric solution to coupled Navier-Stokes/Allen-Cahn equations. SIAM Journal on Mathematical Analysis, 2009, 41(6): 2246-2282
doi: 10.1137/090754698 |
| [2] |
Gal C G, Grasselli M. Longtime behavior for a model of homogeneous incompressible two-phase flows. Discrete and Continuous Dynamical Systems, 2010, 28(1): 1-39
doi: 10.3934/dcds.2010.28.1 |
| [3] |
Zhao L Y, Guo B L, Huang H Y. Vanishing viscosity limit for a coupled Navier-Stokes/Allen-Cahn system. Journal of Mathematical Analysis and Applications, 2011, 384(2): 232-245
doi: 10.1016/j.jmaa.2011.05.042 |
| [4] |
Medjo T T. On the existence and uniqueness of solution to a stochastic  |
| [5] | Zhao X P. Global well-posedness and decay estimates for three-dimensional compressible Navier-Stokes-Allen-Cahn system. Proceedings of the Royal Society of Edinburgh Section A: Mathematics, 2022, 152(5): 1291-1322 |
| [6] | Li Y H, Ding S J, Huang M X. Blow-up criterion for an incompressible Navier-Stokes-Allen-Cahn system with different densities. Discrete and Continuous Dynamical Systems, 2016, 21(5): 1507-1523 |
| [7] |
Chen M T, Guo X W. Global large solutions for a coupled compressible Navier-Stokes/Allen-Cahn system with initial vacuum. Nonlinear Analysis: Real World Applications, 2017, 37: 350-373
doi: 10.1016/j.nonrwa.2017.03.001 |
| [8] | Li Y H, Huang M X. Strong solutions for an incompressible Navier-Stokes-Allen-Cahn system with different densities. Journal of Applied Mathematics and Physics, 2018, 69(3): 1-18 |
| [9] |
Deteix J, Kouamo G, Yakoubi D. Well-posedness of a semi-discrete Navier-Stokes-Allen-Cahn model. Journal of Mathematical Analysis and Applications, 2021, 496(2): 124816
doi: 10.1016/j.jmaa.2020.124816 |
| [10] |
Oleinik O. On the mathematical theory of boundary layer for unsteady flow of incompressible fluid. Journal of Applied Mathematics and Mechanics, 1966, 30(5): 951-974
doi: 10.1016/0021-8928(66)90001-3 |
| [11] |
Liu J G, Xin Z P. Boundary layer behavior in the fluid-dynamic limit for a nonlinear model Boltzmann equation. Archive for Rational Mechanics and Analysis, 1996, 135(1): 61-105
doi: 10.1007/BF02198435 |
| [12] |
Xie X Q. Boundary layers associated with a coupled Navier-Stokes/Allen-Cahn system: the non-characteristic boundary case. Journal of Partial Differential Equations, 2012, 25(1): 66-78
doi: 10.4208/jpde |
| [13] | FAN L L, HOU M C. Asymptotic stability of a boundary layer and rarefaction wave for the outflow problem of the heat-conductive ideal gas without viscosity. Acta Mathematica Scientia, 2020, 40B(6): 1627-1652 |
| [14] | 张浩, 汪娜. 一类弱非线性临界奇摄动积分边界问题. 数学物理学报, 2022, 42A(4): 1060-1073 |
| Zhang H, Wang N. A class of weakly nonlinear critical singularly perturbed integral boundary problems. Acta Mathematica Scientia, 2022, 42A(4): 1060-1073 | |
| [15] | Chorin A J, Marsden J E. A Mathematical Introduction to Fluid Mechanics. New York: Springer-Verlag, 1997 |
| [16] |
Ghil M, Ma T, Wang S H. Structural bifurcation of  doi: 10.1137/S0036139903438818 |
| [17] | Ma T, Wang S H. Rigorous Characterization of Boundary Layer Separations. Cambridge: Proceedings Second MIT Conference on Computational Fluid and Solid Mechanics, 2003 |
| [18] |
Ghil M, Liu J G, Wang C, Wang S H. Boundary-layer separation and adverse pressure gradient for  doi: 10.1016/j.physd.2004.06.012 |
| [19] |
Luo H, Wang Q, Ma T. A predicable condition for boundary layer separation of  doi: 10.1016/j.nonrwa.2014.09.007 |
| [20] |
Wang Q, Luo H, Ma T. Boundary layer separation of 2-D incompressible dirichlet flows. Discrete and Continuous Dynamical Systems B, 2015, 20(2): 675-682
doi: 10.3934/dcdsb.2015.20.675 |
| [21] | 姜倩. 阻尼 Navier-Stokes 系统的渐近吸引子与边界层分离. 四川师范大学学报, 2020, 182(3): 96-102 |
| Jiang Q. The asymptotic attractor of and boundary layer separtion of the damped Navier-Stokes system. Journal of Sichuan Normal University, 2020, 182(3): 96-102 | |
| [22] |
Shen W M, Wang Y, Zhang Z F. Boundary layer separation and local behavior for the steady Prandtl equation. Advances in Mathematics, 2021, 389: 107896
doi: 10.1016/j.aim.2021.107896 |
| [23] |
Ma T, Wang S. Boundary layer separation and structural bifurcation for  doi: 10.3934/dcdsa |
| [24] | Ma T, Wang S H. Geometric theory of incompressible flows with applications to fluid Dynamics. Providence: American Mathematics Society, 2005 |
| [1] | Rui Xu,Yan Yang. Dynamics of an HTLV-I Infection Model with Delayed and Saturated CTL Immune Response and Immune Impairment [J]. Acta mathematica scientia,Series A, 2022, 42(6): 1836-1848. |
| [2] | Xueli Jiang,Xuan Deng,Qiuhao Wen,Yanqin Xiong. Limit Circle Bifurcations of Polynomial Differential System with Two Parallel Switch Straight Lines [J]. Acta mathematica scientia,Series A, 2022, 42(2): 353-364. |
| [3] | Daoxiang Zhang,Ben Li,Dandan Chen,Yating Lin,Xinmei Wang. Hopf Bifurcation for a Fractional Differential-Algebraic Predator-Prey System with Time Delay and Economic Profit [J]. Acta mathematica scientia,Series A, 2022, 42(2): 570-582. |
| [4] | Yue Sun,Daoxiang Zhang,Wen Zhou. The Influence of Fear Effect on Stability Interval of Reaction-Diffusion Predator-Prey System with Time Delay [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1980-1992. |
| [5] | Xin Xie,Jianquan Li,Yuping Wang,Dian Zhang. A Qualitative Analysis of a Tumor-Immune System with Antigenicity [J]. Acta mathematica scientia,Series A, 2021, 41(6): 1969-1979. |
| [6] | Bin Long,Shanshan Xu,Hui Cao,Jianquan Li. The Influence of Splitting Index on Heteroclinic Orbit Bifurcation Under Periodic Perturbation [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1516-1528. |
| [7] | Jingnan Wang,Dezhong Yang. Stability and Bifurcation of a Pathogen-Immune Model with Delay and Diffusion Effects [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1204-1217. |
| [8] | Leta Temesgen Desta,Wenjun Liu,Jian Ding. Dynamics of Traveling Wave Solutions to Fully Nonlinear Heavy Ion-Acoustic Degenerate Relativistic Quantum Plasmas [J]. Acta mathematica scientia,Series A, 2021, 41(2): 496-506. |
| [9] | Gaihui Guo,Xiaohui Liu. Hopf Bifurcation and Stability for an Autocatalytic Reversible Biochemical Reaction Model [J]. Acta mathematica scientia,Series A, 2021, 41(1): 166-177. |
| [10] | Mingmin Wang,Gao Jia. Bifurcation of Positive Solutions for Quasilinear Elliptic Equations with Φ-Laplacian Operator and Concave-Convex Nonlinearities [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1235-1247. |
| [11] | Haixia Li. Existence and Uniqueness of Positive Solutions to an Unstirred Chemostat with Toxins [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1175-1185. |
| [12] | Wang Lingjun, Wang Qiusi. Small-Amplitude Solitary Interfacial Traveling Waves in a Gravity-Capillary Two-Layered Fluid with Vorticity [J]. Acta mathematica scientia,Series A, 2020, 40(4): 947-976. |
| [13] | Yi Shao,Chunxiang A. Limit Cycles Bifurcations of Liénard System of Degree Four with One Nilpotent Cusp [J]. Acta mathematica scientia,Series A, 2020, 40(3): 619-630. |
| [14] | Xue Zhang,Yuhuai Sun. Dynamical Analysis and Traveling Wave Solutions for Generalized (3+1)-Dimensional Kadomtsev-Petviashvili Equation [J]. Acta mathematica scientia,Series A, 2019, 39(3): 501-509. |
| [15] | Hailong Yuan,Yuping Wang,Yanling Li. Positive Solutions of a Predator-Prey Model with Cross Diffusion [J]. Acta mathematica scientia,Series A, 2019, 39(3): 545-559. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 359
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 87
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||