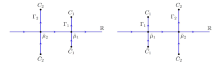
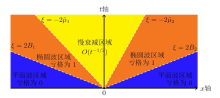
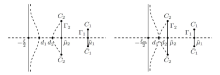
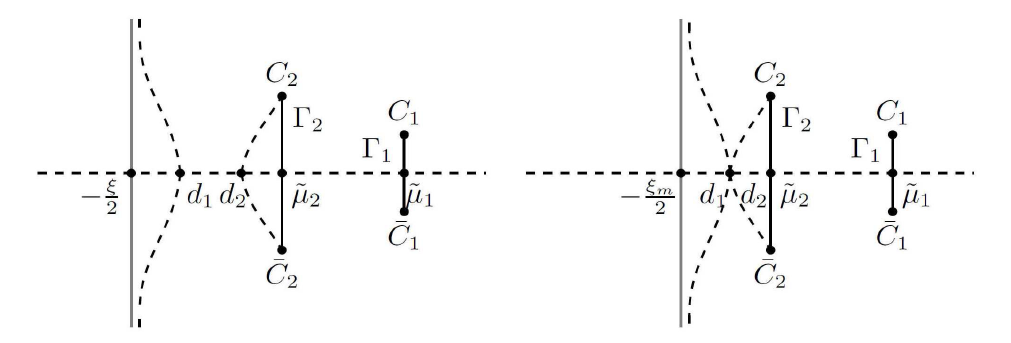
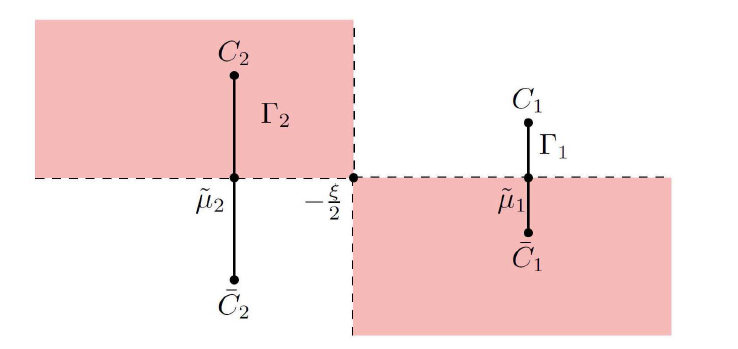
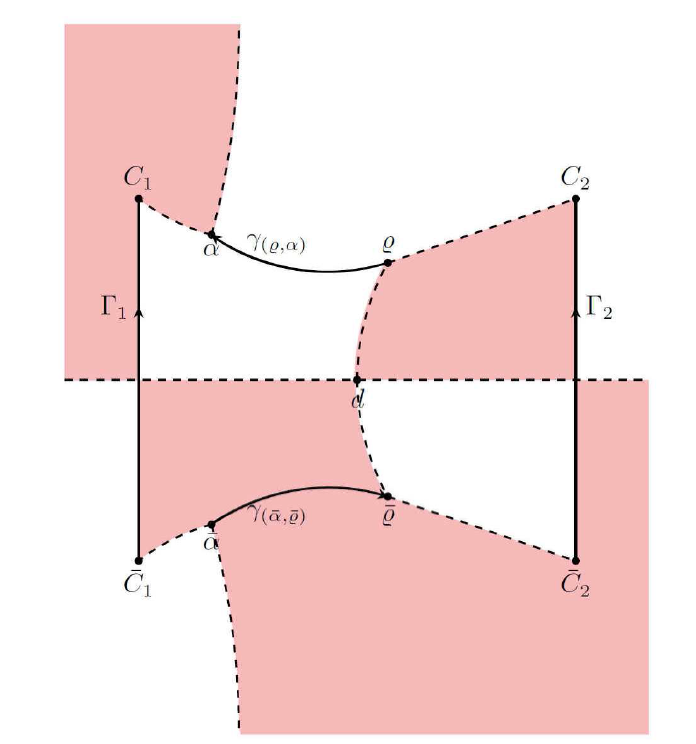
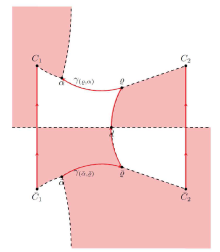
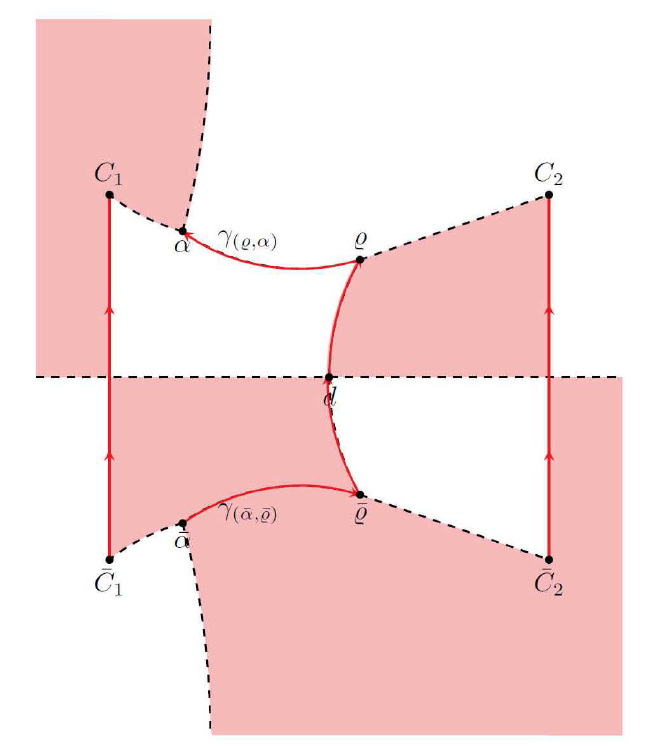
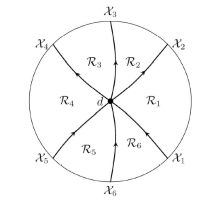
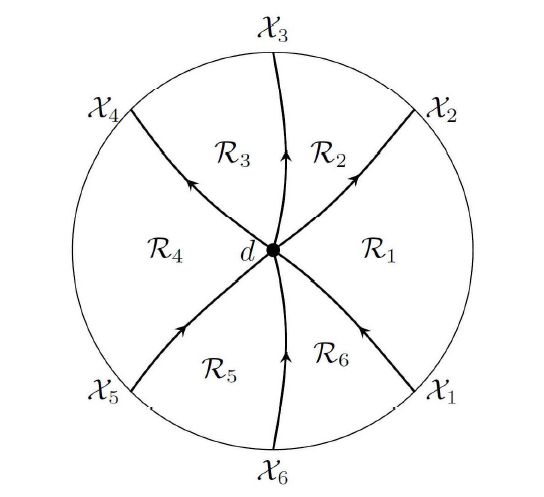
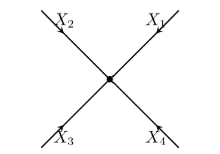
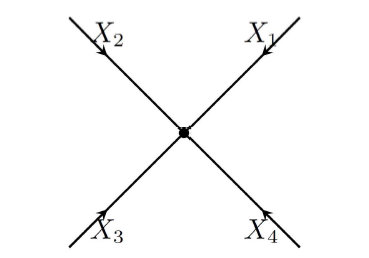
Acta mathematica scientia,Series A ›› 2023, Vol. 43 ›› Issue (4): 1085-1122.
Previous Articles Next Articles
Inverse Scattering Transform for the Focusing Kundu-Eckhaus Equation: Long-time Dynamics of the Steplike Oscillating Background
Wang Guixian1( ),Wang XiuBin2(
),Wang XiuBin2( ),Han Bo1,*(
),Han Bo1,*( )
)
- 1School of Mathematics, Harbin Institute of Technology, Harbin 150001
2School of Mathematics and Institute of Mathematical Physics, China University of Mining and Technology, Jiangsu Xuzhou 221116
-
Received:2022-03-24Revised:2023-01-10Online:2023-08-26Published:2023-07-03 -
Contact:Bo Han E-mail:guixianwang@hit.edu.cn;xbwang@cumt.edu.cn;bohan@hit.edu.cn -
Supported by:NSFC(12271129);NSFC(12201622)
CLC Number:
- O175.2
Cite this article
Wang Guixian,Wang XiuBin,Han Bo. Inverse Scattering Transform for the Focusing Kundu-Eckhaus Equation: Long-time Dynamics of the Steplike Oscillating Background[J].Acta mathematica scientia,Series A, 2023, 43(4): 1085-1122.
share this article
| [1] |
Zakharov V E. Stability of periodic waves of finite amplitudeon the surfaceof a deepfluid. J Appl Mech Tech Phys, 1968, 9: 190-194
doi: 10.1007/BF00913182 |
| [2] | Agrawal G P. Nonlinear Fiber Optics. New York: Academic Press, 1995 |
| [3] |
Bao W Z, Dong X C, Xin J. Comparisons between sine-Gordon and perturbed nonlinear Schrödinger equations for modeling light bullets beyond critical collapse. Physica D, 2010, 239: 1120-1134
doi: 10.1016/j.physd.2010.03.002 |
| [4] | Hasegawa A, Kodama Y. Solitons in Optical Communications. Oxford: Oxford University Press, 1995 |
| [5] | Akhmediev N, Ankiewicz A. Solitons: Nonlinear Pulses and Beams. London: Chapmanand Hall, 1997 |
| [6] | Pitaevskii L, Stringari S. Bose-Einstein Condensation. Oxford: Oxford University Press, 2003 |
| [7] |
Antoine X, Bao W Z, Besse C. Computational methods for the dynamics of the nonlinear Schrödinger/Gross-Pitaevskii equations. Computer Physics Communications, 2013, 184: 2621-2633
doi: 10.1016/j.cpc.2013.07.012 |
| [8] |
Yan Z. Financial rogue waves. Commun Theor Phys, 2010, 54: 947-949
doi: 10.1088/0253-6102/54/5/31 |
| [9] |
Kundu A. Landau-Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations. J Math Phys, 1984, 25: 3433
doi: 10.1063/1.526113 |
| [10] |
Ma W X. Darboux transformations for a Lax integrable system in 2n-dimensions. Lett Math Phys, 1997, 39: 33-49
doi: 10.1007/s11005-997-3049-3 |
| [11] | Matveev V B, Salle M A. Darboux Transformations and Solitons. Berlin: Springer, 1991 |
| [12] |
Tian S F, Zhang H Q. Soliton solutions by Darboux transformation and some reductions for a new Hamiltonian lattice hierarchy. Phys Scr, 2010, 82: 015008
doi: 10.1088/0031-8949/82/01/015008 |
| [13] |
Geng X G, Tam H W. Darboux transformation and soliton solutions for generalized nonlinear Schrödinger equations. J Phys Soc Jpn, 1999, 68: 1508
doi: 10.1143/JPSJ.68.1508 |
| [14] |
Zhao L C, Liu C, Yang Z Y. The rogue waves with quintic nonlinearity and nonlinear dispersion effects in nonlinear optical fibers. Commun Nonlinear Sci Numer Simul, 2015, 20: 9-13
doi: 10.1016/j.cnsns.2014.04.002 |
| [15] |
Wang X, Yang B, Chen Y, Yang Y Q. Higher-order rogue wave solutions of the Kundu-Eckhaus equation. Phys Scr, 2014, 89: 095210
doi: 10.1088/0031-8949/89/9/095210 |
| [16] |
Wang G X, Wang X B, Han B, Xue Q. Inverse scattering method for the Kundu-Eckhaus equation with zero/nonzero boundary conditions. Z Naturforsch A, 2021, 76(4): 315-327
doi: 10.1515/zna-2020-0327 |
| [17] | Ablowitz M J, Segur H. Solitons and the Inverse Scattering Transform. Philadelphia: SIAM, 1981 |
| [18] |
Ablowitz M J, Feng B F, Luo X D, Musslimani Z H. Inverse scattering transform for the nonlocal reverse space-time nonlinear Schrödinger equation. Theor Math Phys, 2018, 196(3): 1241-1267
doi: 10.1134/S0040577918090015 |
| [19] |
Gardner C S, Greene J M, Kruskal M D, Miura R M. Method for solving the Korteweg-de Vries equation. Phys Rev Lett, 1967, 19: 1095-1097
doi: 10.1103/PhysRevLett.19.1095 |
| [20] |
Ma W X, Huang Y H, Wang F D. Inverse scattering transforms and soliton solutions of nonlocal reverse-space nonlinear Schrödinger hierarchies. Stud Appl Math, 2020, 145: 563-585
doi: 10.1111/sapm.v145.3 |
| [21] |
Deift P, Zhou X. A steepest descent method for oscillatory Riemann-Hilbert problems. Ann Math, 1993, 137(2): 295-368
doi: 10.2307/2946540 |
| [22] |
Deift P, Venakides S, Zhou X. The collisionless shock region for the long-time behavior of solutions of the KdV equation. Commun Pure Appl Math, 1994, 47(2): 199-206
doi: 10.1002/(ISSN)1097-0312 |
| [23] |
De Monvel A B, Lenells J, Shepelsky D. The focusing NLS equation with step-like oscillating background: scenarios of long-time asymptotics. Commun Math Phys, 2021, 383: 893-952
doi: 10.1007/s00220-021-03946-x |
| [24] |
De Monvel A B, Lenells J, Shepelsky D. The focusing NLS equation with step-like oscillating background: the genus 3 sector. Commun Math Phys, 2022, 390(3): 1081-1148
doi: 10.1007/s00220-021-04288-4 |
| [25] | De Monvel A B, Kotlyarov V P, Shepelsky D. Focusing NLS equation: long-time dynamics of step-like initial data. Int Math Res Not, 2011, 7: 1613-1653 |
| [26] |
De Monvel A B, Its A, Kotlyarov V. Long-time asymptotics for the focusing NLS equation with time-periodic boundary condition on the half-line. Comm Math Phys, 2009, 290: 479-522
doi: 10.1007/s00220-009-0848-7 |
| [27] |
Buckingham R, Venakides S. Long-time asymptotics of the nonlinear Schrödinger equation Shock problem. Comm Pure Appl Math, 2007, 60(9): 1349-1414
doi: 10.1002/(ISSN)1097-0312 |
| [28] |
Biondini G, Mantzavinos D. Long-time asymptotics for the focusing nonlinear Schrödinger equation with nonzero boundary conditions at infinity and asymptotic stage of modulational instability. Comm Pure Appl Math, 2017, 70(12): 2300-2365
doi: 10.1002/cpa.v70.12 |
| [29] |
Biondini G, Fagerstrom E. The integrable nature of modulational instability. SIAM J Appl Math, 2015, 75: 136-163
doi: 10.1137/140965089 |
| [30] |
Biondini G, Mantzavinos D. Universal nature of the nonlinear stage of modulational instability. Phys Rev Lett, 2016, 116(4): 043902
doi: 10.1103/PhysRevLett.116.043902 |
| [31] |
Xu J, Fan E G, Chen Y. Long-time asymptotic for the derivative nonlinear Schrödinger equation with step-like initial value. Math Phys Anal Geom, 2013, 16: 253-288
doi: 10.1007/s11040-013-9132-3 |
| [32] | Yamane H. Long-time asymptotics for the defocusing integrable discrete nonlinear Schrödinger equation. J Math Soc Jpn, 2014, 6: 765-803 |
| [33] |
Lenells J. The nonlinear steepest descent method: asymptotics for initial-boundary value problems. SIAM J Math Anal, 2016, 48: 2076-2118
doi: 10.1137/15M1036889 |
| [34] |
Rybalko Y, Shepelsky D. Asymptotic stage of modulation instability for the nonlocal nonlinear Schrödinger equation. Physica D, 2021, 428: 133060
doi: 10.1016/j.physd.2021.133060 |
| [35] | Tian S F, Zhang T T. Long-time asymptotic behavior for the Gerdjikov-Ivanov type of derivative nonlinear Schrödinger equation with time-periodic boundary condition. P Am Math Soc, 2018, 146(4): 1713-1729 |
| [36] |
Wang X B, Han B. Long-time behavior for the Cauchy problem of the 3-component Manakov system. Phys Scr, 2020, 95: 065226
doi: 10.1088/1402-4896/ab85ff |
| [37] | Wang X B, Han B. The nonlinear steepest descent approach for long time behavior of the two-component coupled Sasa-Satsuma equation with a 5×5 Lax pair. Taiwanese J Math, 2021, 25(2): 381-407 |
| [38] |
Wang X B, Han B. A Riemann-Hilbert approach to a generalized nonlinear Schrödinger equation on the quarter plane. Math Phys Anal Geom, 2020, 23: 25
doi: 10.1007/s11040-020-09347-1 |
| [39] |
Guo B L, Nan L. Long-time asymptotics for the Kundu-Eckhaus equation on the half-line. J Math Phys, 2018, 59: 061505
doi: 10.1063/1.5020996 |
| [40] |
Wang D S, Wang X L. Long-time asymptotics and the bright N-soliton solutions of the Kundu-Eckhaus equation via the Riemann-Hilbert approach. Nonlinear Anal Real World Appl, 2018, 41: 334-361
doi: 10.1016/j.nonrwa.2017.10.014 |
| [41] |
Wang D S, Guo B L, Wang X L. Long-time asymptotics of the focusing Kundu-Eckhaus equation with nonzero boundary conditions. J Differential Equations, 2019, 266: 5209-5253
doi: 10.1016/j.jde.2018.10.053 |
| [42] |
Lenells J. The nonlinear steepest descent method for Riemann-Hilbert problems of low regularity. Indiana Math J, 2017, 66(4): 1287-1332
doi: 10.1512/iumj.2017.66.6078 |
| [43] |
Lenells J. Matrix Riemann-Hilbert problems with jumps across Carleson contours. Monatsh Math, 2018, 186(1): 111-152
doi: 10.1007/s00605-017-1019-0 pmid: 31258193 |
| [44] | Its A R. Asymptotics of solutions of the nonlinear Schrödinger equation and isomonodromic deformations of systems of linear differential equations. Dokl akad nauk Sssr, 1981, 24: 452-456 |
| [45] |
Zakharov V E, Ostrovsky L A. Modulation instability: the beginning. Physica D, 2009, 238: 540-548
doi: 10.1016/j.physd.2008.12.002 |
| [1] | Wang Xiubin, Tian Shoufu. Exotic Dynamics of Freak Waves in the Focusing Kundu-Eckhaus Equation [J]. Acta mathematica scientia,Series A, 2023, 43(3): 785-794. |
| [2] | Wang Chunjiang, Zhang Jian. Simple-Pole and Double-Pole Solutions for the Mixed Chen-Lee-Liu Derivative Nonlinear Schrödinger Equation with Nonzero Boundary Conditions [J]. Acta mathematica scientia,Series A, 2023, 43(1): 101-122. |
| [3] | Beibei Hu,Ling Zhang,Ning Zhang. An Initial-Boundary Value Problem for the Higher-Order Chen-Lee-Liu Equation on the Half-Line [J]. Acta mathematica scientia,Series A, 2020, 40(2): 422-431. |