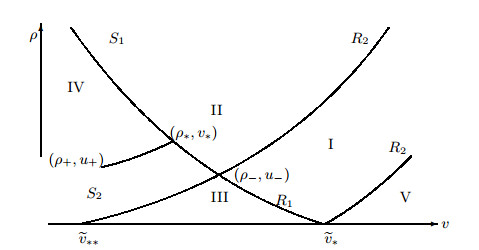
Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (4): 1150-1172.
Previous Articles Next Articles
Concentration and Cavitation in the Pressureless Limit of Euler Equations of Compressible Fluid Flow with Damping and Friction
- School of Mathematics and Statistics, Fuzhou University, Fuzhou 350108
-
Received:2021-09-24Online:2022-08-26Published:2022-08-08 -
Supported by:the NSF of Fujian Province(2019J01642)
CLC Number:
- O175.29
Cite this article
Zhiqiang Shao. Concentration and Cavitation in the Pressureless Limit of Euler Equations of Compressible Fluid Flow with Damping and Friction[J].Acta mathematica scientia,Series A, 2022, 42(4): 1150-1172.
share this article
| 1 | Chaplygin S . On gas jets. Sci Mem Moscow Univ Math Phys, 1904, 21: 1- 121 |
| 2 |
Tsien H S . Two dimensional subsonic flow of compressible fluids. J Aeron Sci, 1939, 6: 399- 407
doi: 10.2514/8.916 |
| 3 |
Von Karman T . Compressibility effects in aerodynamics. J Aeron Sci, 1941, 8: 337- 356
doi: 10.2514/8.10737 |
| 4 | Shen C . The Riemann problem for the pressureless Euler system with the Coulomb-like friction term. IMA J Appl Math, 2016, 81: 76- 99 |
| 5 | Faccanoni G , Mangeney A . Exact solution for granular flows. Int J Numer Anal Meth Geomech, 2012, 37: 1408- 1433 |
| 6 | Earnshaw S . On the mathematical theory of sound. Philos Trans, 1858, 150: 1150- 1154 |
| 7 |
Lu Y G . Existence of global entropy solutions to a nonstrictly hyperbolic system. Arch Ration Mech Anal, 2005, 178: 287- 299
doi: 10.1007/s00205-005-0379-0 |
| 8 |
Cheng Z . Global entropy solutions to a variant of the compressible Euler equations. Appl Math Lett, 2008, 21: 410- 415
doi: 10.1016/j.aml.2007.03.022 |
| 9 |
Klainerman S , Majda A . Singular limits of quasilinear hyperbolic systems with large parameters and the incompressible limit of compressible fluids. Comm Pure Appl Math, 1981, 34: 481- 524
doi: 10.1002/cpa.3160340405 |
| 10 |
Oelschläger K . On the connection between Hamiltonian many-particle systems and the hydrodynamical equation. Arch Ration Mech Anal, 1991, 115: 297- 310
doi: 10.1007/BF00375277 |
| 11 |
Oelschläger K . An integro-differential equation modelling a Newtonian dynamics and its scaling limit. Arch Ration Mech Anal, 1997, 137: 99- 134
doi: 10.1007/s002050050024 |
| 12 |
Caprino S , Esposito R , Marra R , Pulvirenti M . Hydrodynamic limits of the Vlasov equation. Comm Partial Differential Equations, 1993, 18: 805- 820
doi: 10.1080/03605309308820951 |
| 13 | Cheng H , Yang H , Zhang Y . Riemann problem for the Chaplygin Euler equations of compressible fluid flow. Int J Nonlinear Sci Numer Simul, 2010, 11: 985- 992 |
| 14 |
DiPerna R J . Global solutions to a class of nonlinear hyperbolic systems of equations. Comm Pure Appl Math, 1973, 26: 1- 28
doi: 10.1002/cpa.3160260102 |
| 15 |
Li C Z . Existence in the large for certain systems of quasi linear hyperbolic conservation laws. J Differential Equations, 1982, 45: 85- 102
doi: 10.1016/0022-0396(82)90056-0 |
| 16 |
Pang Y , Zhang Y , Wen Y . Delta shock wave to the compressible fluid flow with the generalized Chaplygin gas. Int J Nonlinear Mech, 2018, 99: 311- 318
doi: 10.1016/j.ijnonlinmec.2017.12.014 |
| 17 | Sarrico C O R , Paiva A . The multiplication of distributions in the study of a Riemann problem in fluid dynamics. J Nonlinear Math Phys, 2017, 24: 328- 345 |
| 18 |
Song G , Xiao J . Existence of global weak solutions to a special system of Euler equation with a source (Ⅱ): General case. J Math Anal Appl, 2009, 352: 943- 953
doi: 10.1016/j.jmaa.2008.11.051 |
| 19 |
Sheng S , Shao Z . Concentration of mass in the pressureless limit of the Euler equations of one-dimensional compressible fluid flow. Nonlinear Analysis: Real World Applications, 2020, 52: 103039
doi: 10.1016/j.nonrwa.2019.103039 |
| 20 |
Sheng S , Shao Z . The limits of Riemann solutions to Euler equations of compressible fluid flow with a source term. Journal of Engineering Mathematics, 2020, 125: 1- 22
doi: 10.1007/s10665-020-10066-3 |
| 21 |
Savage S B , Hutter K . The motion of a finite mass of granular material down a rough incline. J Fluid Mech, 1989, 199: 177- 215
doi: 10.1017/S0022112089000340 |
| 22 |
Shen C . The Riemann problem for the Chaplygin gas equations with a source term. Z Angew Math Mech, 2016, 96: 681- 695
doi: 10.1002/zamm.201500015 |
| 23 |
Sun M . The exact Riemann solutions to the generalized Chaplygin gas equations with friction. Commun Nonlinear Sci Numer Simul, 2016, 36: 342- 353
doi: 10.1016/j.cnsns.2015.12.013 |
| 24 |
Daw D A E , Nedeljkov M . Shadow waves for pressureless gas balance laws. Appl Math Lett, 2016, 57: 54- 59
doi: 10.1016/j.aml.2016.01.004 |
| 25 | Edwards C M , Howison S D , Ockendon H , Ockendon J R . Non-classical shallow water flows. IMA J Appl Math, 2008, 73: 137- 157 |
| 26 |
Guo L , Li T , Yin G . The limit behavior of the Riemann solutions to the generalized Chaplygin gas equations with a source term. J Math Anal Appl, 2017, 455: 127- 140
doi: 10.1016/j.jmaa.2017.05.048 |
| 27 |
Guo L , Li T , Yin G . The vanishing pressure limits of Riemann solutions to the Chaplygin gas equations with a source term. Commun Pure Appl Anal, 2017, 16: 295- 309
doi: 10.3934/cpaa.2017014 |
| 28 |
Zhang Y , Zhang Y . Riemann problems for a class of coupled hyperbolic systems of conservation laws with a source term. Commun Pure Appl Anal, 2019, 18: 1523- 1545
doi: 10.3934/cpaa.2019073 |
| 29 |
Zhang Y , Zhang Y . The Riemann problem for the Suliciu relaxation system with the double-coefficient Coulomb-like friction terms. Int J Non-Linear Mech, 2019, 116: 200- 210
doi: 10.1016/j.ijnonlinmec.2019.07.004 |
| 30 |
Zhang Y , Zhang Y , Wang J . Zero-exponent limit to the extended Chaplygin gas equations with friction. Bull Malays Math Sci Soc, 2021, 44: 3571- 3599
doi: 10.1007/s40840-021-01133-8 |
| 31 |
Zhang Q . Concentration in the flux approximation limit of Riemann solutions to the extended Chaplygin gas equations with friction. J Math Phys, 2019, 60: 101508
doi: 10.1063/1.5085233 |
| 32 |
Yin G , Chen J . Existence and stability of Riemann solution to the Aw-Rascle model with friction. Indian J Pure Appl Math, 2018, 49: 671- 688
doi: 10.1007/s13226-018-0294-3 |
| 33 |
Sheng S , Shao Z . The vanishing adiabatic exponent limits of Riemann solutions to the isentropic Euler equations for power law with a Coulomb-like friction term. J Math Phys, 2019, 60: 101504
doi: 10.1063/1.5108863 |
| 34 |
Bourgault Y , Habashi W G , Dompierre J , Baruzzi G S . A finite element method study of Eulerian droplets impingement models. Internat. J Numer Methods Fluids, 1999, 29: 429- 449
doi: 10.1002/(SICI)1097-0363(19990228)29:4<429::AID-FLD795>3.0.CO;2-F |
| 35 | Boutanios Z, Bourgault Y, Cober S, et al. 3D droplets impingement analysis around an aircraft's nose and cockpit using FENSAP-ICE[C]//36th AIAA Aerospace Science Meeting and Exhibit, Reno, NV, USA, 1998. DOI: 10.2514/6.1998-200 |
| 36 | Bourgault Y, Thiriet M. Critical aspects of flow and aerosol simulations in the airway tract[C]//European Conference on Computational Fluid Dynamics-ECCOMAS CFD 2008, Venice, Italy, 2008 |
| 37 |
Keita S , Bourgault Y . Eulerian droplet model: Delta-shocks and solution of the Riemann problem. J Math Anal Appl, 2019, 472: 1001- 1027
doi: 10.1016/j.jmaa.2018.11.061 |
| 38 | Bourgault Y. Computing gas-particle flows in airways with an Eulerian model[C]//European Conference on Computational Fluid Dynamics - ECCOMAS CFD 2006, Egmond ann Zee, The Netherlands, 2006 |
| 39 |
Keita S , Bourgault Y . Eulerian models with particle pressure for air-particle flows. European Journal of Mechanics-/B Fluids, 2019, 78: 263- 275
doi: 10.1016/j.euromechflu.2019.08.001 |
| 40 |
Chen G Q , Liu H . Formation of δ -shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids. SIAM J Math Anal, 2003, 34: 925- 938
doi: 10.1137/S0036141001399350 |
| 41 |
Chen G Q , Liu H . Concentration and cavitation in the vanishing pressure limit of solutions to the Euler equations for nonisentropic fluids. Phys D, 2004, 189: 141- 165
doi: 10.1016/j.physd.2003.09.039 |
| 42 |
Li J . Note on the compressible Euler equations with zero temperature. Appl Math Lett, 2001, 14: 519- 523
doi: 10.1016/S0893-9659(00)00187-7 |
| 43 |
Ibrahim M , Liu F , Liu S . Concentration of mass in the pressureless limit of Euler equations for power law. Nonlinear Anal Real World Appl, 2019, 47: 224- 235
doi: 10.1016/j.nonrwa.2018.10.015 |
| 44 |
Li H , Shao Z . Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for generalized Chaplygin gas. Commun Pure Appl Anal, 2016, 15: 2373- 2400
doi: 10.3934/cpaa.2016041 |
| 45 |
Shen C . The limits of Riemann solutions to the isentropic magnetogasdynamics. Appl Math Lett, 2011, 24: 1124- 1129
doi: 10.1016/j.aml.2011.01.038 |
| 46 |
Shen C , Sun M . Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model. J Differential Equations, 2010, 249: 3024- 3051
doi: 10.1016/j.jde.2010.09.004 |
| 47 |
Shen C , Sun M , Wang Z . Limit relations for three simple hyperbolic systems of conservation laws. Math Methods Appl Sci, 2010, 33: 1317- 1330
doi: 10.1002/mma.1248 |
| 48 |
Sun M . Concentration and cavitation phenomena of Riemann solutions for the isentropic Euler system with the logarithmic equation of state. Nonlinear Anal Real World Appl, 2020, 53: 103068
doi: 10.1016/j.nonrwa.2019.103068 |
| 49 |
Tong M , Shen C . The limits of Riemann solutions for the isentropic Euler system with extended Chaplygin gas. Applicable Analysis, 2019, 98: 2668- 2687
doi: 10.1080/00036811.2018.1469009 |
| 50 |
Sheng W , Wang G , Yin G . Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes. Nonlinear Anal Real World Appl, 2015, 22: 115- 128
doi: 10.1016/j.nonrwa.2014.08.007 |
| 51 |
Sun M . The limits of Riemann solutions to the simplified pressureless Euler system with flux approximation. Math Methods Appl Sci, 2018, 41: 4528- 4548
doi: 10.1002/mma.4912 |
| 52 |
Yang H , Wang J . Delta shocks and vacuum states in vanishing pressure limits of solutions to the isentropic Euler equations for modified Chaplygin gas. J Math Anal Appl, 2014, 413: 800- 820
doi: 10.1016/j.jmaa.2013.12.025 |
| 53 |
Yang H , Zhang Y . Flux approximation to the isentropic relativistic Euler equations. Nonlinear Anal, 2016, 133: 200- 227
doi: 10.1016/j.na.2015.12.002 |
| 54 |
Yin G , Sheng W . Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for polytropic gases. J Math Anal Appl, 2009, 355: 594- 605
doi: 10.1016/j.jmaa.2009.01.075 |
| 55 | Yin G , Sheng W . Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations. Chin Ann Math, 2008, 29B: 611- 622 |
| 56 |
Yin G , Sheng W . Delta wave formation and vacuum state in vanishing pressure limit for system of conservation laws to relativistic fluid dynamics. Z Angew Math Mech, 2015, 95: 49- 65
doi: 10.1002/zamm.201200148 |
| 57 |
Zhang Y , Yang H . Flux-approximation limits of solutions to the relativistic Euler equations for polytropic gas. J Math Anal Appl, 2016, 435: 1160- 1182
doi: 10.1016/j.jmaa.2015.11.012 |
| 58 | Zhang Y , Zhang Y . Delta-shocks and vacuums in the relativistic Euler equations for isothermal fluids with the flux approximation. J Math Phys, 2019, 60: 011508 |
| 59 | Sheng W, Zhang T. The Riemann Problem for the Transportation Equations in Gas Dynamics. Providence, RI: Amer Math Soc, 1999 |
| 60 | Joseph K T . A Riemann problem whose viscosity solutions contain delta measures. Asymptot Anal, 1993, 7: 105- 120 |
| [1] | Yuan-an Zhao,Gaowei Cao,Xiaozhou Yang. Global Singular Structures of Non-Selfsimilar Riemann Solutions for Two Dimensional Non-homogeneous Burgers Equation [J]. Acta mathematica scientia,Series A, 2022, 42(4): 1122-1149. |
| [2] | Ning-An LAI, Wei XIANG, Yi ZHOU. GLOBAL INSTABILITY OF MULTI-DIMENSIONAL PLANE SHOCKS FOR ISOTHERMAL FLOW [J]. Acta mathematica scientia,Series A, 2022, 42(3): 887-902. |
| [3] | Jia Jia. The Two-Dimensional Steady Chaplygin Gas Flows Passing a Straight Wedge [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1270-1282. |
| [4] | Yufeng Chen,Tingting Chen,Zhen Wang. The Existence of the Measure Solution for the Non-Isentropic Chaplygin Gas [J]. Acta mathematica scientia,Series A, 2020, 40(4): 833-841. |
| [5] | Qingling Zhang,Ying Ba. The Perturbed Riemann Problem for the Pressureless Euler Equations with a Flocking Dissipation [J]. Acta mathematica scientia,Series A, 2020, 40(1): 49-62. |
| [6] | Lijun Pan,Xinli Han,Tong Li. The Generalized Riemann Problem for Chromatography Equations with Delta Shock Wave [J]. Acta mathematica scientia,Series A, 2019, 39(6): 1300-1313. |
| [7] | Chen Tingting, Qu Aifang, Wang Zhen. The Two-Dimensional Riemann Problem for Isentropic Chaplygin Gas [J]. Acta mathematica scientia,Series A, 2017, 37(6): 1053-1061. |
| [8] | Li Huahui, Shao Zhiqiang. Vanishing Pressure Limit of Riemann Solutions to the Aw-Rascle Model for Generalized Chaplygin Gas [J]. Acta mathematica scientia,Series A, 2017, 37(5): 917-930. |
| [9] | Li Huahui, Shao Zhiqiang. Interactions of Delta Shock Waves for the Nonsymmetric Keyfitz-Kranzer System with Split Delta Functions [J]. Acta mathematica scientia,Series A, 2017, 37(4): 714-729. |
| [10] | SHAO Zhi-Qiang. The Riemann Problem with Delta Initial Data for the Aw-Rascle Traffic Model with Chaplygin Pressure [J]. Acta mathematica scientia,Series A, 2014, 34(6): 1353-1371. |
| [11] | LI Jian-Ye, SHAO Zhi-Qiang. The Riemann Problem with Delta Initial Data for the Zero-Pressure Relativistic Euler Equations Hyperbolic Systems of Conservation Laws [J]. Acta mathematica scientia,Series A, 2014, 34(5): 1083-1092. |
| [12] | LIU Jian, LIAN Ru-Xu, QIAN Mao-Fu. Global Existence of Solution to Bipolar Navier-Stokes-Poisson System [J]. Acta mathematica scientia,Series A, 2014, 34(4): 960-976. |
| [13] | LIU Xiao-Min, WANG Zhen. The Riemann Problem for a System of Nonlinear Elasticity of |Mixed Type [J]. Acta mathematica scientia,Series A, 2013, 33(5): 801-818. |
| [14] | ZHANG Ting-Ting. The Stability of the Riemann Solutions for Aw-Rascle Model [J]. Acta mathematica scientia,Series A, 2013, 33(2): 230-241. |
| [15] | Liu Fagui; Ge Yunfei; Li Caizhong. Linear Hyperbolic Systems with Discontinuous Coefficients [J]. Acta mathematica scientia,Series A, 2007, 27(1): 184-192. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 138
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 122
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|