Acta mathematica scientia,Series A ›› 2021, Vol. 41 ›› Issue (5): 1311-1322.
Previous Articles Next Articles
Finite Difference Scheme for the Nonhomogeneous Initial Boundary Value Problem of Critical Schrödinger Map
Haiyun Deng1( ),Hui Liu2,*(
),Hui Liu2,*( ),Wenjing Song3(
),Wenjing Song3( )
)
- 1 Department of Applied Mathematics, Nanjing Audit University, Nanjing 211815
2 School of Mathematical Sciences, Qufu Normal University, Shandong Qufu 273165
3 College of Science, Xi'an Polytechnic University, Xi'an 710048
-
Received:2020-08-13Online:2021-10-26Published:2021-10-08 -
Contact:Hui Liu E-mail:haiyundengmath1989@njust.edu.cn;liuhuinanshi@qfnu.edu.cn;wenjingsong1@163.com -
Supported by:the NSFC(12001276);the NSFC(12001275);the NSFC(12071219);the NSFC(11901342);the NSFC(12001415);the NSF of Shandong Province(ZR2018QA002);the China Postdoctoral Science Foundation(2019M652350)
CLC Number:
- O241.82
Cite this article
Haiyun Deng,Hui Liu,Wenjing Song. Finite Difference Scheme for the Nonhomogeneous Initial Boundary Value Problem of Critical Schrödinger Map[J].Acta mathematica scientia,Series A, 2021, 41(5): 1311-1322.
share this article
"
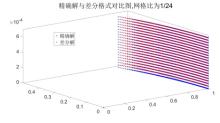
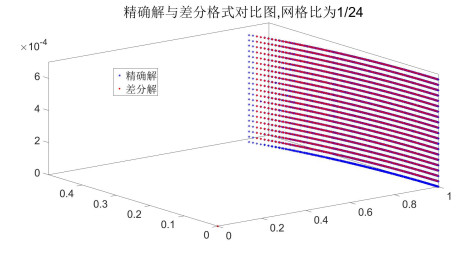
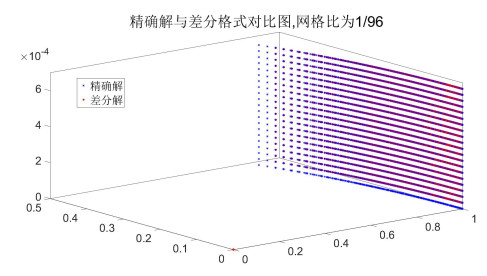
| 时间层 | 精确解 | 差分格式解 | 误差值 | 所需时间(s) |
| 1 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.017160 |
| 2 | 1.00+e00 | 1.00-3.33067e-16 | 3.33067e-16 | 0.012998 |
| 3 | 1.00+e00 | 1.00-3.33067e-16 | 3.33067e-16 | 0.011783 |
| 4 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011667 |
| 5 | 1.00+e00 | 1.00-6.66134e-16 | 6.66134e-16 | 0.011951 |
| 6 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011711 |
| 7 | 1.00+e00 | 1.00-3.33067e-16 | 3.33067e-16 | 0.011630 |
| 8 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011647 |
| 9 | 1.00+e00 | 1.00-5.55112e-16 | 5.55112e-16 | 0.011787 |
| 10 | 1.00+e00 | 1.00-5.55112e-16 | 5.55112e-16 | 0.011690 |
| 11 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011579 |
| 12 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011576 |
| 13 | 1.00+e00 | 1.00-3.33067e-16 | 3.33067e-16 | 0.011611 |
| 14 | 1.00+e00 | 1.00-3.33067e-16 | 3.33067e-16 | 0.011501 |
| 15 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011609 |
| 16 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011973 |
| 17 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011524 |
| 18 | 1.00+e00 | 1.00-3.33067e-16 | 3.33067e-16 | 0.012638 |
| 19 | 1.00+e00 | 1.00-4.44089e-16 | 4.44089e-16 | 0.011606 |
| 20 | 1.00+e00 | 1.00-3.33067e-16 | 3.33067e-16 | 0.011690 |
| 1 |
Angenent S B , Hulshof J , Matano H . The radius of vanishing bubbles in equivariant harmonic map flow from D2 to S2. SIAM J Math Anal, 2009, 41 (3): 1121- 1137
doi: 10.1137/070706732 |
| 2 | Bejenaru I , Ionescu A D , Kenig C E , Tataru D . Global Schrödinger maps in dimensions d ≥ 2:small data in the critical Sobolev spaces. Ann of Math, 2011, 173 (2): 1443- 1506 |
| 3 |
Cimrák I . Convergence result for the constraint preserving mid-point scheme for micromagnetism. J Comput Appl Math, 2009, 228 (1): 238- 246
doi: 10.1016/j.cam.2008.09.017 |
| 4 |
Dodson B , Smith P . A controlling norm for energy-critical Schrödinger maps. Trans Amer Math Soc, 2015, 367 (10): 7193- 7220
doi: 10.1090/S0002-9947-2015-06417-4 |
| 5 |
E W N , Wang X P . Numerical methods for the Landau-Lifshitz equation. SIAM J Numer Anal, 2000, 38 (5): 1647- 1665
doi: 10.1137/S0036142999352199 |
| 6 | Gilbarg D , Trudinger N S . Elliptic Partial Differential Equations of Second Order. New York: Springer-Verlag, 1983 |
| 7 |
Guo B L , Han Y Q . Global smooth solution of hydrodynamical equation for the Heisenberg paramagnet. Math Methods Appl Sci, 2004, 27 (2): 181- 191
doi: 10.1002/mma.450 |
| 8 |
Gustafson S , Kang K , Tsai T P . Schrödinger flow near harmonic maps. Comm Pure Appl Math, 2007, 60 (4): 463- 499
doi: 10.1002/cpa.20143 |
| 9 | Gustafson S , Kang K , Tsai T P . Asymptotic stability of harmonic maps under the Schrödinger flow. Duke Math J, 2008, 145 (3): 537- 583 |
| 10 |
Gustafson S , Kang K , Tsai T P . Asymptotic stability, concentration, and oscillation in harmonic map heat-flow, Landau-Lifshitz, and Schrödinger maps on   doi: 10.1007/s00220-010-1116-6 |
| 11 |
Jendrej J . Construction of two-bubble solutions for the energy-critical NLS. Anal PDE, 2017, 10 (8): 1923- 1959
doi: 10.2140/apde.2017.10.1923 |
| 12 |
Kim E , Lipnikov K . The mimetic finite difference method for the Landau-Lifshitz equation. J Comput Phys, 2017, 328, 109- 130
doi: 10.1016/j.jcp.2016.10.016 |
| 13 | Kim E. Numerical Methods for the Landau-Lifshitz Equation in Micromagnetics: The Mimetic Finite Difference Method and the Mass-Lumped Finite Element Method[D]. Berkeley: University of California, 2017 |
| 14 | Krieger J , Miao S . On the stability of blowup solutions for the critical corotational wave-map problem. Duke Math J, 2020, 169 (3): 435- 532 |
| 15 |
Li Z , Zhao L F . Convergence to harmonic maps for the Landau-Lifshitz flows between two dimensional hyperbolic spaces. Discrete Contin Dyn Syst, 2019, 39 (1): 607- 638
doi: 10.3934/dcds.2019025 |
| 16 |
Li P C , Xie C J , Du R , et al. Two improved Gauss-Seidel projection methods for Landau-Lifshitz-Gilbert equation. J Comput Phys, 2020, 401, 109046
doi: 10.1016/j.jcp.2019.109046 |
| 17 | 陆金甫, 关治. 偏微分方程数值解法. 北京: 清华大学出版社, 2004 |
| Lu J F , Guan Z . Numerical Solution of Partial Differential Equations. Beijing: Tsinghua University Press, 2004 | |
| 18 | 吕永强. Landau-Lifshitz方程的有限差分格式与整体正则解[D]. 北京: 中国工程物理研究院, 2004 |
| Lv Y Q. Finite Difference Format and the Overall Regular Solutions of Landau-Lifshitz Equations[D]. Beijing: Chinese Research Institute of Engineering Physics, 2004 | |
| 19 |
Merle F , Raphaël P , Rodnianski I . Blowup dynamics for smooth data equivariant solutions to the critical Schrödinger map problem. Invent Math, 2013, 193 (2): 249- 365
doi: 10.1007/s00222-012-0427-y |
| 20 |
Mu C L , Liu L M , Wu Y H , Yan L . Some new results for the multidimensional Landau-Lifshitz equations. Phys Lett A, 2008, 372 (43): 6469- 6474
doi: 10.1016/j.physleta.2008.09.006 |
| 21 |
Perelman G . Blow up dynamics for equivariant critical Schrödinger maps. Comm Math Phys, 2014, 330 (1): 69- 105
doi: 10.1007/s00220-014-1916-1 |
| 22 |
Sanchez D . Numerical study of long waves in ferromagnetic media. Numer Methods Partial Differential Equations, 2006, 22 (5): 1127- 1148
doi: 10.1002/num.20142 |
| 23 |
van den Berg J B , Hulshof J , King J R . Formal asymptotics of bubbling in the harmonic map heat flow. SIAM J Appl Math, 2003, 63 (5): 1682- 1717
doi: 10.1137/S0036139902408874 |
| 24 | 杨干山, 刘宪高. Landau-Lifshitz方程派生的球面锥对称族及其演化. 中国科学: 数学, 2011, 41 (2): 181- 196 |
| Yang G S , Liu X G . Spherical cone symmetric families generated by Landau-Lifshitz equation and their evolution. Sci Sin Math, 2011, 41 (2): 181- 196 | |
| 25 |
Yang G S . The difference between Schrödinger equation derived from Schrödinger map and Landau-Lifshitz equation. Phys Lett A, 2012, 376 (4): 231- 235
doi: 10.1016/j.physleta.2011.11.003 |
| 26 | 杨干山, 吴继晖, 郭柏灵. 具有二阶逼近效应场多维Landau-Lifshitz方程解的极限行为. 中国科学: 数学, 2013, 43, 445- 476 |
| Yang G S , Wu J H , Guo B L . Limiting behavior of solutions to multidimensional Landau-Lifshitz equations with second approximation of effective field. Sci Sin Math, 2013, 43, 445- 476 | |
| 27 |
Yang W , Wang D L , Yang L . A stable numerical method for space fractional Landau-Lifshitz equations. Appl Math Lett, 2016, 61, 149- 155
doi: 10.1016/j.aml.2016.05.014 |
| 28 | Zhou Y L , Guo B L , Tan S B . Existence and uniqueness of smooth solution for system of ferro-magnetic chain. Sci China Ser A, 1991, 34 (3): 257- 266 |
| [1] | Chen Huaxin, Jia Wensheng. Approximation Theorem and General Convergence of Population Games [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1566-1573. |
| [2] | Feng Zaiyong, Chen Ning, Tai Yongpeng, Xiang Zhengrong. On the Observer Design for Fractional Singular Linear Systems [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1529-1544. |
| [3] | Cheng Yiyuan, Zha Xingxing, Zhang Yongquan. On Stochastic Accelerated Gradient with Convergence Rate of Regression Learning [J]. Acta mathematica scientia,Series A, 2021, 41(5): 1574-1584. |
| [4] | Dongxia Fan,Dongxia Zhao,Na Shi,Tingting Wang. The PDP Feedback Control and Stability Analysis of a Diffusive Wave Equation [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1088-1096. |
| [5] | Yajun Xie. A Class of Efficient Modified Algorithms Based onHalley-Newton Methods [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1066-1078. |
| [6] | Lixiang Feng,Defen Wang. Global Stability of an Epidemic Model with Quarantine and Incomplete Treatment [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1235-1248. |
| [7] | Bin Wu,Qun Chen. Lipschitz Stability for a Transport Coefficient Inverse Problem of a Linearly Coupled Korteweg-de Vries System [J]. Acta mathematica scientia,Series A, 2021, 41(3): 740-761. |
| [8] | Qiulan Qi,Dandan Guo. Approximation Properties of a New Bernstein-Bézier Operators with Parameters [J]. Acta mathematica scientia,Series A, 2021, 41(3): 583-594. |
| [9] | Guodong Ma. Improved PRP and HS Conjugate Gradient Methods with the Strong Wolfe Line Search [J]. Acta mathematica scientia,Series A, 2021, 41(3): 837-847. |
| [10] | Yongjian Liu,Qiujian Huang. Jacobi Analysis of the Rabinovich System [J]. Acta mathematica scientia,Series A, 2021, 41(3): 783-796. |
| [11] | Xiaoni Chi,Rong Zeng,Sanyang Liu,Zhibin Zhu. A Regularized Nonmonotone Inexact Smoothing Newton Algorithm for Weighted Symmetric Cone Complementarity Problems [J]. Acta mathematica scientia,Series A, 2021, 41(2): 507-522. |
| [12] | Xiling Li,Fei Gao,Wenqin Li. Stability Analysis of Fractional-Order Hepatitis B Virus Infection Model With Immune Delay [J]. Acta mathematica scientia,Series A, 2021, 41(2): 562-576. |
| [13] | Juan Wang,Jie Zhao. Homogenization of the Oscillating Robin Mixed Boundary Value Problems [J]. Acta mathematica scientia,Series A, 2021, 41(1): 81-90. |
| [14] | Shenglian Wan. A Double Projection Algorithm for Solving Variational Inequalities [J]. Acta mathematica scientia,Series A, 2021, 41(1): 237-244. |
| [15] | Gaihui Guo,Xiaohui Liu. Hopf Bifurcation and Stability for an Autocatalytic Reversible Biochemical Reaction Model [J]. Acta mathematica scientia,Series A, 2021, 41(1): 166-177. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 156
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 95
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|