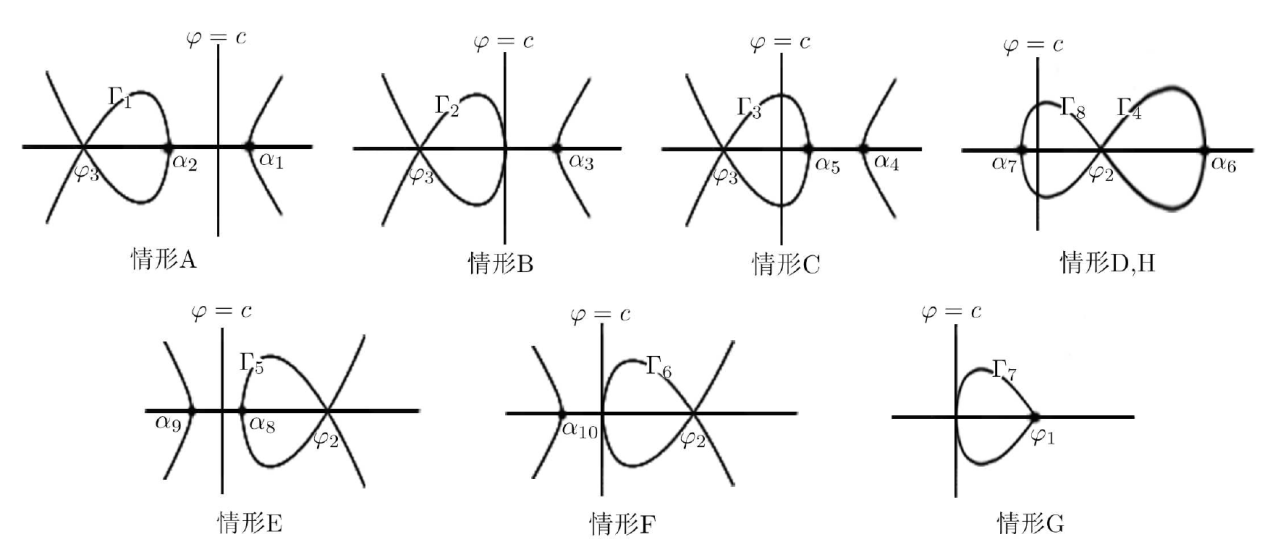
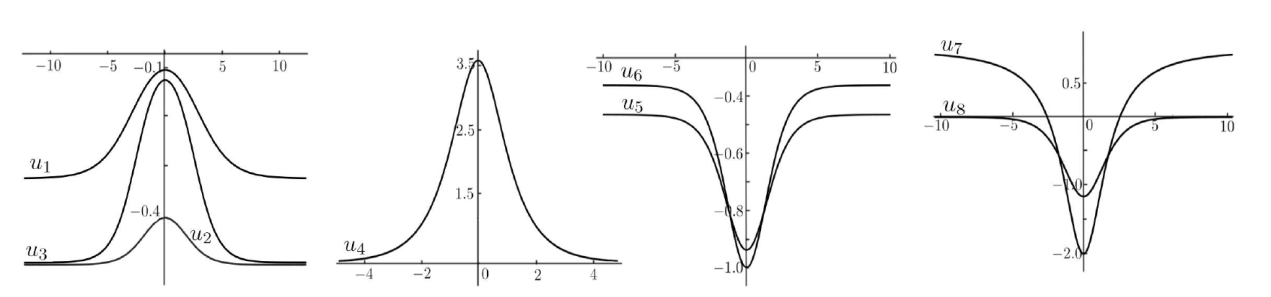
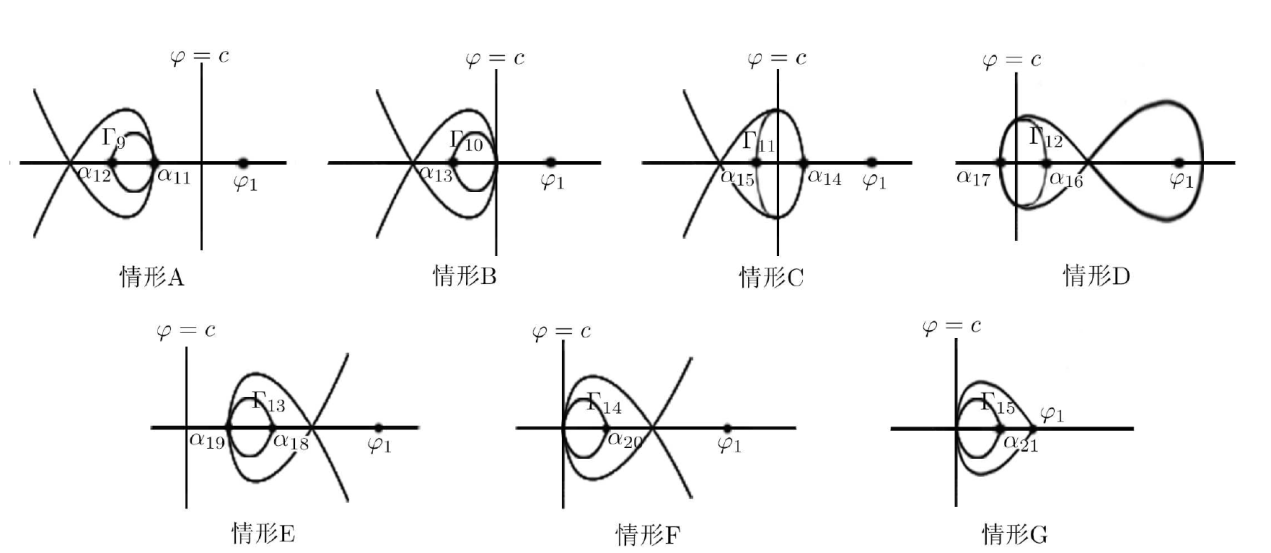
Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (3): 670-686.
Previous Articles Next Articles
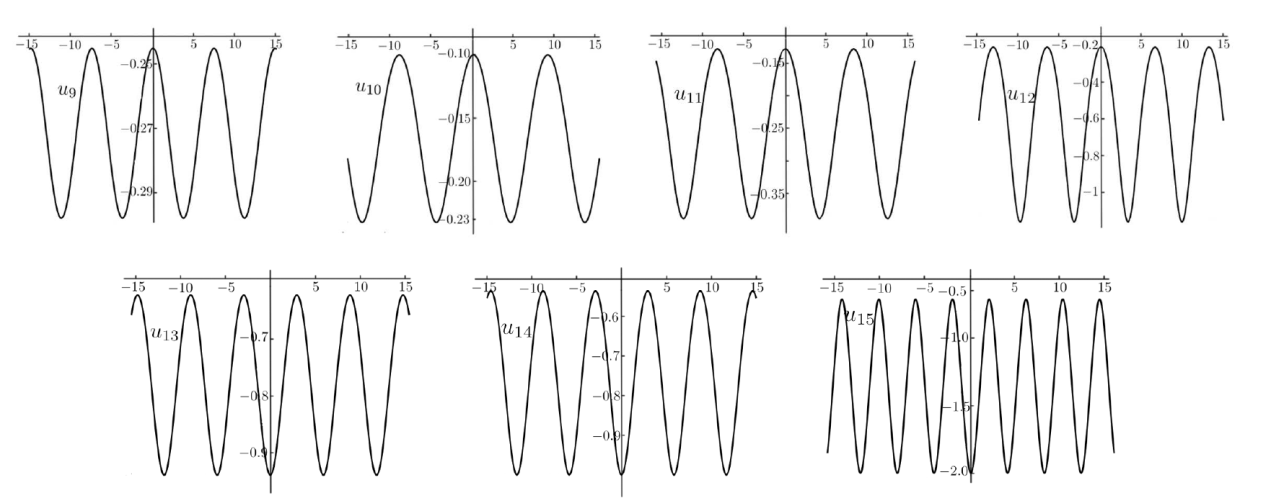
Solitary and Periodic Solutions of the Generalized b-equation
Yang Jiaopeng1( ),Liang Yong2,*(
),Liang Yong2,*( )
)
- 1. School of Mathematics and Statistics, Guangdong University of Foreign Studies, Guangzhou 510006
2. School of Mathematics, South China University of Technology, Guangzhou 510640
-
Received:2023-11-21Revised:2024-01-04Online:2024-06-26Published:2024-05-17 -
Supported by:NSFC(12201136);Foundation for Innovative Young Talents of GuangDong(2021KQNCX019);GuangZhou Basic and Applied Basic Research Foundation(202201010278)
CLC Number:
- O175.2
Cite this article
Yang Jiaopeng, Liang Yong. Solitary and Periodic Solutions of the Generalized b-equation[J].Acta mathematica scientia,Series A, 2024, 44(3): 670-686.
share this article
| [1] |
Camassa R, Holm D D. An integrable shallow water equation with peaked solitons. Phys Rev Lett, 1993, 71: 1661-1664
doi: 10.1103/PhysRevLett.71.1661 pmid: 10054466 |
| [2] | Cooper F, Shepard H. Solitons in the Camassa-Holm shallow water equation. Phys Lett A, 1994, 194: 246-250 |
| [3] | Constantin A, Strauss W A. Stability of peakons. Commun Pur Appl Math, 2000, 53: 603-610 |
| [4] | Degasperis A, Procesi M. Asymptotic integrability. Symmetry and Perturbation Theory, 1999, 1: 23-37 |
| [5] | Lundmark H, Szmigielski J. Multi-peakon solutions of the Degasperis-Procesi equation. Inverse Prob, 2003, 19: 1241-1245 |
| [6] | Chen C, Tang M Y. A new type of bounded waves for Degasperis-Procesi equations. Chaos Solit Fract, 2006, 27: 698-704 |
| [7] |
Guo B L, Liu Z R. Periodic cusp wave solutions and single-solitons for the  |
| [8] |
Li Y. Nonunfiorm dependence for the Cauchy problem of the general  |
| [9] | Freire I L. Remarks on strong global solutions of the b-equation. Appl Math Lett, 2023, 146: 108820 |
| [10] | Tian L X, Song X Y. New peaked solitary wave solutions of the generalized Camassa-Holm equation. Chaos Solit Fract, 2004, 21: 621-637 |
| [11] | Liu Z R, Ouyang Z Y. A note on solitary waves for modified forms of Camassa-Holm and Degasperis-Procesi equations. Phys Lett A, 2007, 366: 377-381 |
| [12] | Khuri S A. New ansatz for obtaining wave solutions of the generalized Camassa-Holm equation. Chaos Solit Fract. 2005, 25: 705-710 |
| [13] | Daros A, Arruda L K. On the instability of elliptic traveling wave solutions of the modified Camassa-Holm equation. J Differ Equations, 2019, 266: 1946-1968 |
| [14] | Zhou Y Q, Chen G R, Li J B. Bifurcations, exact peakon, periodic peakons and solitary wave solutions of the cubic Camassa-Holm type equation. Int J Bifurcat Chaos, 2023, 33: 2350014 |
| [15] | Liu Z R, Tang H. Explicit periodic wave solutions and their bifurcations for generalized Camassa-Holm equation. Int J Bifurcat Chaos, 2010, 20: 2507-2519 |
| [16] | Wazwaz A M. New solitary wave solutions to the modified forms of Degasperis-Procesi and Camassa-Holm equations. Appl Math Comput, 2007, 186: 130-141 |
| [17] |
Chen Y R, Ye W B, Liu R. The explicit periodic wave solutions and their limit forms for a generalized  |
| [18] | Yang J P, Liu R, Chen Y R. Bifurcations of solitary waves of a simple equation. Int J Bifurcat Chaos, 2020, 30: 2050138 |
| [19] |
Yang J P, Li Z G, Liu Z R. The existence and bifurcation of peakon and anti-peakon to the   |
| [20] | Li Z G, Liu R. Bifurcations and exact solutions in a nonlinear wave equation. Int J Bifurcat Chaos, 2019, 29: 1950098 |
| [21] |
Li Z G, Liu R. Blow-up solutions for a case of  |
| [1] | Wang Zihuan,Wang Chao. Symmetric and Periodic Solutions for a Class of Weakly Coupled Systems Composed of Two Particles with Obstacles [J]. Acta mathematica scientia,Series A, 2023, 43(5): 1427-1439. |
| [2] | Tingting Jiang,Zengji Du. Periodic Solutions of a Neutral Impulsive Predator-Prey Model with Holling-Type IV Functional Response [J]. Acta mathematica scientia,Series A, 2021, 41(1): 178-193. |
| [3] | Zhongwei Cao,Xiangdan Wen,Wei Feng,Li Zu. Dynamics of a Nonautonomous SIRI Epidemic Model with Random Perturbations [J]. Acta mathematica scientia,Series A, 2020, 40(1): 221-233. |
| [4] | Chao Wang. Periodic Solutions of a Class of Nonlinear Hill's Type Equations with Bounded Restoring Force [J]. Acta mathematica scientia,Series A, 2019, 39(4): 761-772. |
| [5] | Changqing Tong,Jing Zheng. Periodic Solutions of a Semi-Linear Klein-Gordon Equations with High Frequencies [J]. Acta mathematica scientia,Series A, 2019, 39(3): 484-500. |
| [6] | WANG Xue-Chen, WEI Jun-Jie. The Effect of Delay on a Diffusive Predator-Prey System with Ivlev-Type Functional Response [J]. Acta mathematica scientia,Series A, 2014, 34(2): 234-250. |
| [7] | LI Xiao-Pei. Generalized Homoclinic Solutions for the Stationary Extended Fisher-Kolmogorov Equation [J]. Acta mathematica scientia,Series A, 2014, 34(1): 126-138. |
| [8] | YU Jin-Feng, XUE Xiao-Ping. Existence of Periodic Solution for Evolution Inclusion in Banach Space [J]. Acta mathematica scientia,Series A, 2012, 32(1): 126-136. |
| [9] | CHEN Zhi-Bin, HUANG Li-Hong. Existence and Uniqueness of Periodic Solutions for a Class of Neutral |Differential System [J]. Acta mathematica scientia,Series A, 2010, 30(4): 1094-1101. |
| [10] | YANG Xin-Song, RUI Wei-Guo. Existence and Uniqueness of Positive Periodic Solution for a Kind of Generalized Logistic Model of Single Species [J]. Acta mathematica scientia,Series A, 2009, 29(5): 1442-1452. |
| [11] | WANG Kai. Existence of Periodic Solutions for a Type of High Order Neutral Functional Differential Equations [J]. Acta mathematica scientia,Series A, 2009, 29(3): 794-799. |
| [12] | Xie Qiangjun; Zhang Guangxin; Zhou Zekui. The Existence of Positive Periodic Solutions for a Kind of Periodic Reaction-diffusion Equations [J]. Acta mathematica scientia,Series A, 2009, 29(2): 465-474. |
| [13] | Liu Xiping; Jia Mei; Ren Rui. On the Existence and Uniqueness of Periodic Solutions to a Type [J]. Acta mathematica scientia,Series A, 2007, 27(1): 37-044. |
| [14] | FANG Cong-Na, WANG Quan-Yi. The Existence and Uniqueness and Global Attraction of Periodic Solutions for a Class of Functional Differential Equations [J]. Acta mathematica scientia,Series A, 2005, 25(6): 913-925. |
| [15] | BANG Shi-Guo. Periodic Solutions of Liénard Equations with Delay [J]. Acta mathematica scientia,Series A, 2004, 4(6): 689-693. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 98
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 52
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|