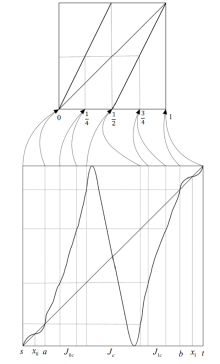
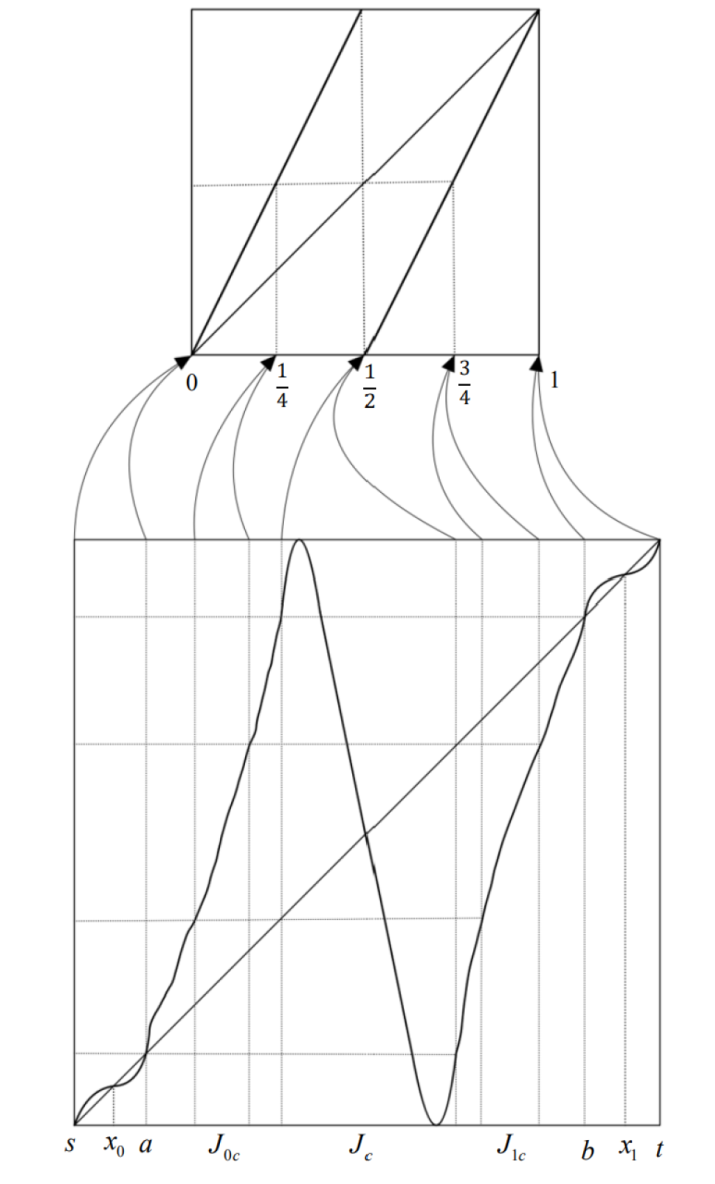
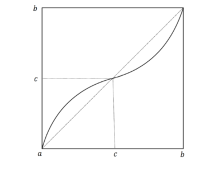
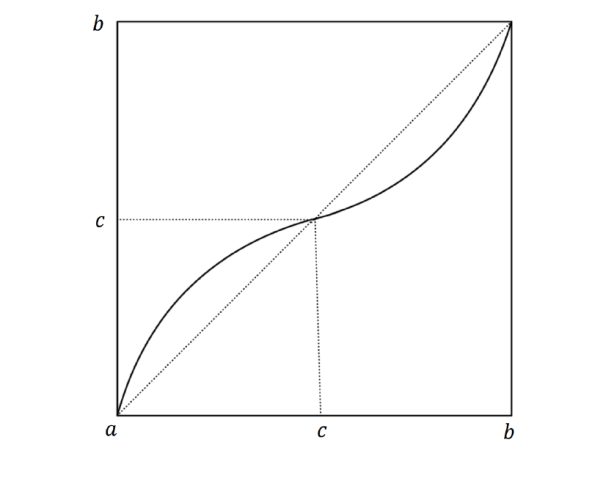
Acta mathematica scientia,Series A ›› 2024, Vol. 44 ›› Issue (1): 1-11.
Robust Accessible Hyperbolic Repelling Sets
- Center for Mathematical Sciences and Department of Mathematics, School of Science, Wuhan University of Technology, Wuhan 430070; School of Mathematical Sciences, Xiamen University, Fujian Xiamen 361005
-
Received:2023-04-23Revised:2023-07-31Online:2024-02-26Published:2024-01-10 -
Supported by:NSFC(12271418)
CLC Number:
- O193
Cite this article
Xiao Jianrong. Robust Accessible Hyperbolic Repelling Sets[J].Acta mathematica scientia,Series A, 2024, 44(1): 1-11.
share this article
| [1] | Blokh A M, Lyubich M Y. Measurable dynamics ofS-unimodal maps of the interval. Annales Scientifiques de l'Ecole Normale Supérieure, 1991, 24(5): 545-573 |
| [2] |
Bowen R. A. Horseshoe with Positive Measure. Inventiones Mathematicae, 1975, 29: 203-204
doi: 10.1007/BF01389849 |
| [3] |
Bruin H. Topological conditions for the existence of absorbing Cantor sets. Transactions of the American Mathematical Society, 1998, 350(6): 2229-2263
doi: 10.1090/tran/1998-350-06 |
| [4] | Bruin H, Keller G, Nowicki T, Strien S V. Wild Cantor attractors exist. Annals of Mathematics, 1996: 97-130 |
| [5] |
Bruin H, Keller G, Pierre M S. Adding machines and wild attractors. Ergodic Theory and Dynamical Systems, 1997, 17(6): 1267-1287
doi: 10.1017/S0143385797086392 |
| [6] |
Bruin H, Todd M. Wild attractors and thermodynamic formalism. Monatshefte für Mathematik, 2015, 178(1): 39-83
doi: 10.1007/s00605-015-0747-2 |
| [7] | De Melo W, Van Strien S. One-Dimensional Dynamics. Berlin: Springer, 2012 |
| [8] | Devaney R L. An Introduction to Chaotic Dynamical Systems. Boca Raton: CRC Press, 2018 |
| [9] | Ding Y, Sun Y. α-limit sets and Lyapunov function for maps with one topological attractor. Acta Mathematica Scientia, 2022, 42B(2): 813-824 |
| [10] |
Ding Y, Xiao J. Thick hyperbolic repelling invariant Cantor sets and wild attractors. Nonlinearity, 2023, 36(2): 1378-1397
doi: 10.1088/1361-6544/acb18f |
| [11] |
Glendinning P. Milnor attractors and topological attractors of a piecewise linear map. Nonlinearity, 2001, 14(2): 239-257
doi: 10.1088/0951-7715/14/2/304 |
| [12] |
Graczyk J, Kozlovski O S. On Hausdorff dimension of unimodal attractors. Communications in Mathematical Physics, 2006, 264(3): 565-581
doi: 10.1007/s00220-006-1540-9 |
| [13] | Kozlovski O S. Getting rid of the negative Schwarzian derivative condition. Annals of Mathematics, 2000: 743-762 |
| [14] |
Li S, Shen W. Hausdorff dimension of Cantor attractors in one-dimensional dynamics. Inventiones Mathematicae, 2008, 171(2): 345-387
doi: 10.1007/s00222-007-0083-9 |
| [15] |
Li S, Shen W. The topological complexity of Cantor attractors for unimodal interval maps. Transactions of the American Mathematical Society, 2016, 368(1): 659-688
doi: 10.1090/tran/2016-368-01 |
| [16] |
Li S, Wang Q. A new class of generalized Fibonacci unimodal maps. Nonlinearity, 2014, 27(7): 1633-1643
doi: 10.1088/0951-7715/27/7/1633 |
| [17] |
Liu J, Shi Y G. Conjugacy problem of strictly monotone maps with only one jump discontinuity. Results in Mathematics, 2020, 75(3): 1-15
doi: 10.1007/s00025-019-1126-4 |
| [18] |
Lyubich M. Combinatorics, geometry and attractors of quasi-quadratic maps. Annals of Mathematics, 1994, 140(2): 347-404
doi: 10.2307/2118604 |
| [19] |
Lyubich M, Milnor J. The Fibonacci unimodal map. Journal of the American Mathematical Society, 1993, 6(2): 425-457
doi: 10.1090/jams/1993-06-02 |
| [20] |
Milnor J. On the concept of attractor. Communications in Mathematical Physics, 1985, 99(2): 177-195
doi: 10.1007/BF01212280 |
| [21] | Murdock J, Botelho F. A map with invariant Cantor set of positive measure. Nonlinear Analysis: Theory, Methods & Applications, 2005, 63(5-7): e659-e668 |
| [1] | Ran Bo,Sun Xiangkai,Guo Xiaole. On Robust Optimal Solutions for a Class of Uncertain Fractional Polynomial Optimization Problems [J]. Acta mathematica scientia,Series A, 2025, 45(2): 630-639. |
| [2] |
Chen Yating, Liu Haiyan, Chen Mi.
|
| [3] | Zhang Yongxue, Jia Wensheng. Stability of Solutions for Controlled Systems of Generalized Multiobjective Multi-Leader-Follower Games Under Bounded Rationality [J]. Acta mathematica scientia,Series A, 2024, 44(6): 1689-1702. |
| [4] | Huang Jiayi, Sun Xiangkai. Duality Characterizations for a Class of Two-Stage Adjustable Robust Multiobjective Programming [J]. Acta mathematica scientia,Series A, 2024, 44(1): 185-194. |
| [5] | Caiyun Xiao,Xiangkai Sun. Characterization of the Radius of the Robust Feasibility for a Class of Uncertain Convex Optimization Problems with Polynomial Constraints [J]. Acta mathematica scientia,Series A, 2022, 42(5): 1551-1559. |
| [6] | Yuan Shi,Yongxia Zhao. α-Robust Optimal Investment Strategy for Target Benefit Pension Plans Under Default Risk [J]. Acta mathematica scientia,Series A, 2022, 42(3): 943-960. |
| [7] | Yuying Zhao,Yuzhen Wen. Optimal Investment and Proportional Reinsurance Strategies to Minimize the Probability of Drawdown Under Ambiguity Aversion [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1147-1165. |
| [8] | Meng Li,Guolin Yu. Optimality of Robust Approximation Solutions for Uncertain Convex Optimization Problems [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1007-1017. |
| [9] | Dongping Ye,Donghui Fang. Lagrange Dualities for Robust Composite Optimization Problems [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1095-1107. |
| [10] | Sun Xiangkai. Characterizations of Robust Solution for Convex Optimization Problems with Data Uncertainty [J]. Acta mathematica scientia,Series A, 2017, 37(2): 257-264. |
| [11] | WANG Hong-Ning, YU Huan-Ran. Robust Nonparametric Regression with Simultaneous Scale Curve Estimation Based on Dependent Observations [J]. Acta mathematica scientia,Series A, 2010, 30(3): 835-847. |
| [12] | XIONG Ming, XIE Min-Yu. The Properties of Statistics of the Mean-mixture of Normal Distribution [J]. Acta mathematica scientia,Series A, 2009, 29(3): 685-690. |
| [13] | Bao Jundong; Deng Feiqi; Luo Qi. Robust Stabilization for Delay Differential Systems Based on SLQ Control [J]. Acta mathematica scientia,Series A, 2007, 27(2): 359-367. |
| [14] | YANG Chang-Li, RUAN Rong-Yao, GONG Miao-Kun. Robust Adaptive State Feedback Controller Design and Analysis of a Class of Uncertain Nonlinear Systems [J]. Acta mathematica scientia,Series A, 2004, 24(1): 26-37. |
| [15] | Huang Changshui Ruan Rongyao. Adaptive Outputfeedback Control of a Class of Nonlinear Systems with bounded disturbances [J]. Acta mathematica scientia,Series A, 2000, 20(3): 405-413. |
|