Acta mathematica scientia,Series A ›› 2022, Vol. 42 ›› Issue (5): 1506-1516.
Previous Articles Next Articles
Algorithm with Order m + 1 Convergence for Weakly Nonlinear Complementarity Problems Derived From the Discretization of Free Boundary Problems
- School of Big Data, Fuzhou University of International Studies and Trade & Engineering Research Center of Universities of Fujian Province, Fuzhou 350202
-
Received:2021-09-26Online:2022-10-26Published:2022-09-30 -
Contact:Changfeng Ma E-mail:xyj@fzfu.edu.cn;mcf@fzfu.edu.cn -
Supported by:the Natural Science Foundation of Fujian Province(2019J01879);the Key Research and Development Projects of University of Chinese Academy of Science(H2020003(20A01246ZY));the Major Educational Reform Projects of Fujian Province(FBJG20200310);the New Engineering Research Practice Project(J15934 19745784GS)
CLC Number:
- O224.2
Cite this article
Yajun Xie,Changfeng Ma. Algorithm with Order m + 1 Convergence for Weakly Nonlinear Complementarity Problems Derived From the Discretization of Free Boundary Problems[J].Acta mathematica scientia,Series A, 2022, 42(5): 1506-1516.
share this article
"
| 初始点 | z(1)0 | z(1)0 | z(2)0 | z(2)0 | |
| 方法 | HONM | FBSN | HONM | FBSN | |
| n=500 | It | 2 | 11 | 3 | 11 |
| CPU | 0.1032 | 0.3788 | 0.1511 | 0.4340 | |
| RES | 6.1815e-016 | 6.6613e-016 | 5.6610e-016 | 1.1047e-015 | |
| n=1000 | It | 2 | 11 | 3 | 11 |
| CPU | 0.5880 | 1.1551 | 0.8808 | 1.3629 | |
| RES | 6.1815e-016 | 6.6613e-016 | 5.6610e-016 | 1.1047e-015 | |
| n=2000 | It | 2 | 11 | 3 | 11 |
| CPU | 3.2900 | 4.2802 | 5.1104 | 5.2537 | |
| RES | 6.1815e-016 | 6.6613e-016 | 5.6610e-016 | 1.1047e-015 | |
| n=2500 | It | 2 | 11 | 3 | 11 |
| CPU | 5.9151 | 6.4952 | 6.0723 | 8.0709 | |
| RES | 6.1815e-016 | 6.6613e-016 | 5.6610e-016 | 1.1047e-015 |
"
| 初始点 | z(1)0 | z(1)0 | z(2)0 | z(2)0 | |
| 算法 | HONM | CBSN | HONM | CBSN | |
| n=800 | It | 2 | 3 | 3 | 4 |
| CPU | 0.3332 | 0.4838 | 0.4840 | 0.6879 | |
| RES | 6.1815e-016 | 2.1678e-016 | 5.6610e-016 | 2.7616e-016 | |
| n=1500 | It | 2 | 3 | 3 | 4 |
| CPU | 1.5395 | 2.3335 | 2.3196 | 3.0597 | |
| RES | 6.1815e-016 | 2.1678e-016 | 5.6610e-016 | 2.7616e-016 | |
| n=3000 | It | 2 | 3 | 3 | 4 |
| CPU | 10.4229 | 15.6110 | 15.6472 | 20.6621 | |
| RES | 6.1815e-016 | 2.1678e-016 | 5.6610e-016 | 2.7616e-016 | |
| n=5000 | It | 2 | 3 | 3 | 4 |
| CPU | 45.8406 | 65.4892 | 69.7337 | 89.2019 | |
| RES | 6.1815e-016 | 2.1678e-016 | 5.6610e-016 | 2.7616e-016 |
"
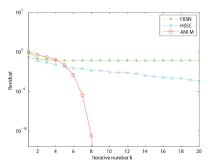
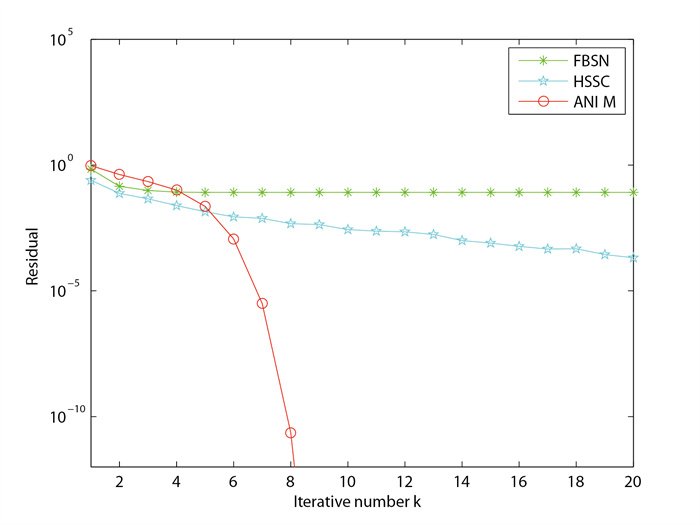
| 初始点 | z(1)0 | z(1)0 | z(2)0 | z(2)0 | |
| 算法 | n=225 | n=961 | n=2209 | n=3969 | |
| FBSN | It | 151 | 151 | 151 | 151 |
| CPU | 4.7936 | 29.2284 | 254.8708 | 1458.9 | |
| RES | 8.2364e-002 | 8.3124e-002 | 8.342e-002 | 8.333e-002 | |
| MMSA | It | 104 | 393 | 853 | 401 |
| CPU | 0.0326 | 2.3810 | 26.8192 | 40.3858 | |
| RES | 8.7282e-013 | 9.9680e-013 | 9.7832e-013 | 9.8603e-013 | |
| HONM | It | 9 | 9 | 2 | 2 |
| CPU | 0.0617 | 2.1585 | 3.3131 | 16.6964 | |
| RES | 0 | 0 | 0 | 0 |
"
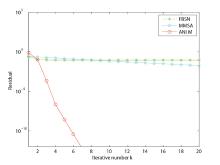
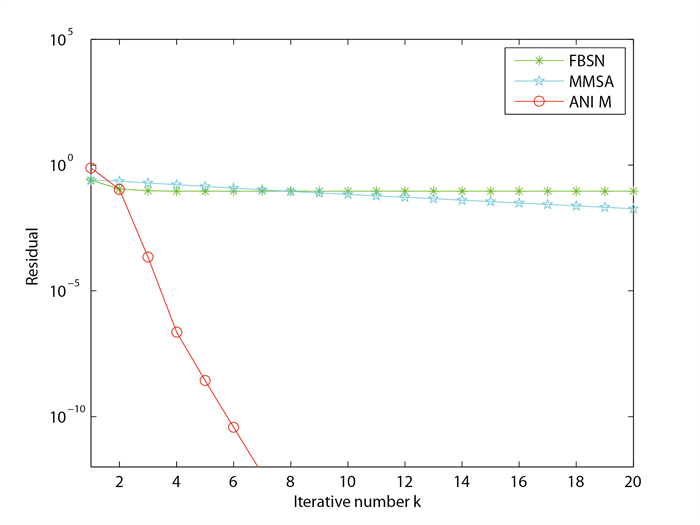
| 初始点 | z(1)0 | z(1)0 | z(2)0 | z(2)0 | |
| 算法 | n=225 | n=961 | n=2209 | n=3969 | |
| FBSN | It | 151 | 151 | 151 | 151 |
| CPU | 4.8202 | 31.4063 | 305.5803 | 1539.5 | |
| RES | 9.1410e-002 | 9.2369e-002 | 9.231e-002 | 9.261e-002 | |
| MMSA | It | 105 | 396 | 314 | 404 |
| CPU | 0.0317 | 2.3881 | 8.3169 | 36.5056 | |
| RES | 8.0910e-013 | 9.4929e-013 | 9.2611e-013 | 9.8210e-013 | |
| HONM | It | 7 | 7 | 2 | 2 |
| CPU | 0.0498 | 1.5487 | 2.1063 | 11.0249 | |
| RES | 1.1757e-015 | 1.0710e-016 | 0 | 0 |
"
| 初始点 | z(3)0 | z(3)0 | z(2)0 | z(2)0 | |
| 算法 | n=225 | n=961 | n=2209 | n=3969 | |
| FBSN | It | 151 | 151 | 151 | 151 |
| CPU | 4.8505 | 31.2633 | 263.0305 | 1266.1 | |
| RES | 9.1410e-002 | 9.2369e-002 | 4.1121e-002 | 4.2001e-002 | |
| MMSA | It | 105 | 227 | 299 | 388 |
| CPU | 0.0244 | 1.4172 | 9.3599 | 37.8653 | |
| RES | 8.0910e-013 | 9.9726e-013 | 9.0592e-013 | 9.7484e-013 | |
| HONM | It | 2 | 2 | 2 | 2 |
| CPU | 0.0157 | 0.3998 | 2.2060 | 10.6302 | |
| RES | 0 | 0 | 0 | 0 |
"
| 初始点 | z(3)0 | z(3)0 | z(2)0 | z(2)0 | |
| 算法 | n=225 | n=961 | n=2209 | n=3969 | |
| FBSN | It | 8 | 9 | 10 | 10 |
| CPU | 0.0534 | 1.4129 | 13.8041 | 81.8000 | |
| RES | 1.3059e-008 | 1.5371e-007 | 7.4532e-008 | 4.8048e-007 | |
| MMSA | It | 114 | 222 | 297 | 388 |
| CPU | 0.0273 | 1.3339 | 9.3883 | 41.4062 | |
| RES | 8.9631e-013 | 9.6913e-013 | 9.9131e-013 | 9.2350e-013 | |
| HONM | It | 2 | 2 | 2 | 2 |
| CPU | 0.0156 | 0.3238 | 2.1165 | 12.1649 | |
| RES | 0 | 0 | 0 | 0 |
| 1 |
Bai Z Z . Modulus-based matrix splitting iteration methods for linear complementarity problems. Numer Linear Algebra Appl, 2010, 17, 917- 933
doi: 10.1002/nla.680 |
| 2 |
Bai Z Z . On the convergence of the multisplitting methods for the linear complementarity problem. SIAM J Matrix Anal Appl, 1999, 21, 67- 78
doi: 10.1137/S0895479897324032 |
| 3 | Bai Z Z . Experimental study of the asynchronous multisplitting relaxtation methods for linear complementarity problems. J Comput Math, 2002, 20, 561- 574 |
| 4 |
Bai Z Z , Evans D J . Matrix multisplitting relaxtion methods for linear complementarity problem. Inter J Comput Math, 1997, 63, 309- 326
doi: 10.1080/00207169708804569 |
| 5 | Bai Z Z , Evans D J . Matrix multisplitting methods with applications to linear complementarity problems: Parallel synchronous and chaotic methods. Calculateurs Parallelés Réseaux et Systémes Répartis, 2001, 13, 125- 154 |
| 6 | Bai Z Z , Evans D J . Parallel chaotic multisplitting iterative methods for the large spase linear complementarity problem. J Comput Math, 2001, 19, 281- 292 |
| 7 |
Bai Z Z , Evans D J . Matrix multisplitting methods with applications to linear complementarity problems: Parallel asynchronous methods. Int J Comput Math, 2002, 79, 205- 232
doi: 10.1080/00207160211927 |
| 8 | Bai Z Z , Huang Y G . A class of asynchronous iterations for the linear complementarity problem. J Comput Math, 2003, 21, 773- 790 |
| 9 |
Bai Z Z , Zhang L L . Modulus-based synchronous multisplitting iteration methods for linear complementarity problems. Numer Linear Algebra Appl, 2013, 20, 425- 439
doi: 10.1002/nla.1835 |
| 10 |
Chen X , Nashed Z , Qi L . Smoothing methods and semismooth methods for nondifferentiable operator equations. SIAM J Numer Anal, 2000, 38, 1200- 1216
doi: 10.1137/S0036142999356719 |
| 11 | Cottle R W , Pang J S , Stone RE . The Linear Complementarity Problem. Boston: Academic Press, 1992 |
| 12 |
Cryer C . The solution of a quadratic programming using systematic overrelaxation. SIAM J Control Optim, 1971, 9, 385- 392
doi: 10.1137/0309028 |
| 13 |
Fischer A . A special Newton-type optimization method. Optim, 1992, 24, 269- 284
doi: 10.1080/02331939208843795 |
| 14 |
Foutayeni Y E L , Khaladi M . Using vector divisions in solving the linear complementarity problem. J Comput Appl Math, 2012, 236, 1919- 1925
doi: 10.1016/j.cam.2011.11.001 |
| 15 | Huang B H , Xie Y J , Ma C F . Krylov subspace methods to solve a class of tensor equations via the Einstein product. Numer Linear Algebra Appl, 2019, 26 (4): e2254 |
| 16 |
Huang N , Ma C F . The modulus-based matrix splitting algorithms for a class of weakly nonlinear complementarity problems. Numer Linear Algebra Appl, 2016, 23, 558- 569
doi: 10.1002/nla.2039 |
| 17 | 黄象鼎, 曾钟钢, 马亚南. 非线性数值分析的理论与方法. 武汉: 武汉大学出版社, 2004 |
| Huang X D , Zeng Z G , Ma Y N . The Theory and Methods for Nonlinear Numerical Analysis. Wuhan: University of Wuhan Press, 2004 | |
| 18 |
Jiang H Y , Qi L . A new nonsmooth equations approach to nonlinear complementarity problems. SIAM J Control Optim, 1997, 35, 178- 193
doi: 10.1137/S0363012994276494 |
| 19 |
Lemke C E . Bimatrix equilibrium points and mathematical programming. Management Science, 1965, 11 (7): 681- 689
doi: 10.1287/mnsc.11.7.681 |
| 20 | Luca D , Fancchinei F , Kanzow C . A semismooth equation approach to the solution of nonlinear complementarity problems. Math Program, 1996, 75, 407- 439 |
| 21 | Murty K G . Linear Complementarity, Linear and Nonlinear Programming. Berlin: Heldermann, 1988 |
| 22 |
Qi L , Sun J . A nonsmooth version of Newtons method. Math Programming, 1993, 58, 353- 367
doi: 10.1007/BF01581275 |
| 23 |
Sun Z , Zeng J P . A monotone semismooth Newton type method for a class of complementarity problems. J Comput Appl Math, 2011, 235, 1261- 1274
doi: 10.1016/j.cam.2010.08.012 |
| 24 |
Tseng P . On linear convergence of iterative method for the variational inequality problem. J Comput Appl Math, 1995, 60, 237- 252
doi: 10.1016/0377-0427(94)00094-H |
| 25 | Xie Y J , Ke Y F . Neural network approaches based on new NCP-functions for solving tensor complementarity problem. J Appl Math Comput, 2021, 67, 833- 853 |
| 26 | Yu Z , Qin Y . A cosh-based smoothing Newton method for P0 nonlinear complementarity problem. Nonlinear Anal, Real World Appl, 2011, 12, 875- 884 |
| 27 | Zhang L L . Two-step modulus based matrix splitting iteration for linear complementarity problems. Numer Algoritm, 2011, 57, 83- 99 |
| 28 | Zheng N , Yin J F . Accelerated modulus-based matrix splitting iteration methods for linear complementarity problem. Numer Algoritm, 2011, 57, 83- 99 |
| [1] | Yajun Xie. A Class of Efficient Modified Algorithms Based onHalley-Newton Methods [J]. Acta mathematica scientia,Series A, 2021, 41(4): 1066-1078. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 113
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 81
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|