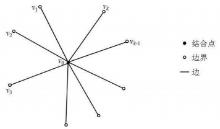
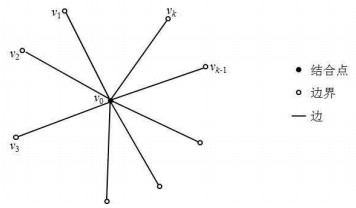
| 1 |
Abbas M I . Existence and uniqueness results for fractional differential equations with Riemann-Liouville fractional integral boundary conditions. Abstract and Applied Analysis, 2015, 2015: 1- 6
|
| 2 |
Agarwal R P , Nieto J J , Zhou Y . A survey on fuzzy fractional differential and optimal control nonlocal evolution equations. Journal of Computational and Applied Mathematics, 2018, 399: 3- 29
|
| 3 |
Amann H . On the number of solutions of nonlinear equations in ordred Banach spaces. Journal of Functional Analysis, 1972, 14: 346- 384
|
| 4 |
Bai Z B , Zhang H Y . Solvability of fractional three-point boundary value problems with nonlinear growth. Applied Mathematics and Computation, 2011, 218 (5): 1719- 1725
doi: 10.1016/j.amc.2011.06.051
|
| 5 |
Berdyshev A B , Cabada A , Turmetov K B . On the solvability of some boundary value problem for polyharmonic equation with boundary operator of a fractional order. Applied Mathematical Modelling, 2015, 39 (15): 4548- 4569
doi: 10.1016/j.apm.2015.01.006
|
| 6 |
Bondarenko N P . A partial inverse problem for the differential pencil on a star-shaped graph. Results in Mathematics, 2017, 72: 1933- 1942
doi: 10.1007/s00025-017-0683-7
|
| 7 |
Caballero J , Harjani J , Sadarangani K . Positive solutions for a class of singular fractional boundary value problems. Computers Mathematics with Applications, 2011, 62: 1325- 1332
doi: 10.1016/j.camwa.2011.04.013
|
| 8 |
Cabada A , Wang J T . Positive solutions of nonlinear fractional differential equations with integral boundary value conditions. Journal of Mathematical Analysis and Applications, 2012, 389 (1): 403- 411
doi: 10.1016/j.jmaa.2011.11.065
|
| 9 |
Cui Y J . Uniqueness of solution for boundary value problems for fractional differential equations. Applied Mathematics Letters, 2016, 51: 48- 54
doi: 10.1016/j.aml.2015.07.002
|
| 10 |
Granas A , Dugundji J . Fixed Point Theory. New York: Springer-Verlag, 2003
|
| 11 |
Graef J R , Kong L , Wang M . Existence and uniqueness of solutions for a fractional boundary value problem on a graph. Fractional Calculus and Applied Analysis, 2014, 17 (2): 499- 510
doi: 10.2478/s13540-014-0182-4
|
| 12 |
Graef J R , Kong L J , Yang B . Positive solutions for a fractional boundary value problem. Applied Mathematics Letters, 2016, 56: 49- 55
doi: 10.1016/j.aml.2015.12.006
|
| 13 |
Ma T T , Tian Y , Zhang Y . Boundary value problem for linear and nonlinear fractional differential equations. Applied Mathematics Letters, 2018, 17: 1- 7
|
| 14 |
Mehandiratta V , Mehra M . A difference scheme for the time-fractional diffusion equation on a metric star graph. Applied Numerical Mathematics, 2020, 158: 152- 163
doi: 10.1016/j.apnum.2020.07.022
|
| 15 |
Mehandiratta V , Mehra M , Leugering G . Existence and uniqueness results for a nonlinear Caputo fractional boundary value problem on a star graph. Journal of Mathematical Analysis and Applications, 2019, 477 (2): 1243- 1264
doi: 10.1016/j.jmaa.2019.05.011
|
| 16 |
Su X W . Boundary value problem for a couple systerm of nonlinear fractional differential equations. Applied Mathematics Letters, 2009, 22: 64- 69
doi: 10.1016/j.aml.2008.03.001
|
| 17 |
Vol'pert A I . Differential equations on graphs. Mathematical Modelling of Natural Phenomena, 2015, 10: 6- 15
|
| 18 |
Wang Y Q , Wang H Q . Triple positive solutions for fractional differential equation boundary value problems at resonance. Applied Mathematics Letters, 2020, 106: 106376
doi: 10.1016/j.aml.2020.106376
|
| 19 |
Xu J F , Wei Z L , Dong W . Uniqueness of positive solutions for a class of fractional boundary value problems. Applied Mathematics Letters, 2012, 25: 590- 593
doi: 10.1016/j.aml.2011.09.065
|
| 20 |
Yang X , Wei Z L , Dong W . Existence of positive solutions for the boundary value problem of nonlinear fractional differential equations. Communications in Nonlinear Science and Numerical Simulation, 2012, 17 (1): 85- 92
doi: 10.1016/j.cnsns.2011.05.007
|
| 21 |
Yong Z . Basic Theory of Fractional Differential Equations. Singapore: World Scientific, 2014
|
| 22 |
Zhang S . Positive solutions for boundary-value problems of nonlinear fractional differential equations. Electronic Journal of Differential Equations, 2006, 2006: 1- 12
|
 ),Huize Cai2,Hujun Yang1
),Huize Cai2,Hujun Yang1