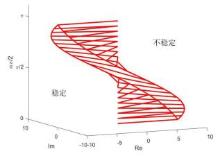
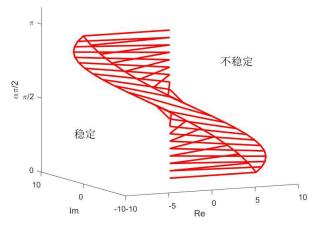
Acta mathematica scientia,Series A ›› 2021, Vol. 41 ›› Issue (2): 562-576.
Stability Analysis of Fractional-Order Hepatitis B Virus Infection Model With Immune Delay
Xiling Li( ),Fei Gao*(
),Fei Gao*( ),Wenqin Li
),Wenqin Li
- Department of Mathematics, College of Science, Wuhan University of Technology, Wuhan 430070
-
Received:2020-02-14Online:2021-04-26Published:2021-04-29 -
Contact:Fei Gao E-mail:lingleah@whut.edu.cn;gaof@whut.edu.cn -
Supported by:the State Key Program of NSFC(91324201);the Fundamental Research Funds for the Central Universities(2018IB017);the NSF of Hubei Province(2014CFB865)
CLC Number:
- O175
Cite this article
Xiling Li,Fei Gao,Wenqin Li. Stability Analysis of Fractional-Order Hepatitis B Virus Infection Model With Immune Delay[J].Acta mathematica scientia,Series A, 2021, 41(2): 562-576.
share this article
| 1 | Marion P L, Robinson W S. Hepadna Viruses: Hepatitis B and Related Viruses//Cooper M, et al. Curr Topic Microbiol Immu, 1983, 105: 99-121 |
| 2 | Lavanchy D . Worldwide epidemiology of HBV infection, disease burden, and vaccine prevention. J Clin Virol, 2005, 34 (Suppl 1): S1- S3 |
| 3 |
Nowak M A , Bonhoeffer S , Hill A M , et al. Viral dynamics in hepatitis B virus infection. Proc Natl Acad Sci, 1996, 93 (9): 4398- 4402
doi: 10.1073/pnas.93.9.4398 |
| 4 |
Nowak M A , Bangham C R M . Population dynamics of immune responses to persistent viruses. Science, 1996, 272 (5258): 74- 79
doi: 10.1126/science.272.5258.74 |
| 5 | Min L Q , Su Y M , Kuang Y . Mathematical analysis of a basic virus infection model with application to HBV infection. Rocky MT J Math, 2008, 38 (5): 1573- 1585 |
| 6 |
Gourley S A , Kuang Y , Nagy J D . Dynamics of a delay differential equation model of hepatitis B virus infection. J Biol Dynam, 2008, 2 (2): 140- 153
doi: 10.1080/17513750701769873 |
| 7 |
马庆波, 向华. 具有时滞的HBV病毒动力学模型稳定性分析. 生物信息学, 2009, 7 (4): 326- 329
doi: 10.3969/j.issn.1672-5565.2009.04.022 |
|
Ma Q B , Xiang H . Stability analysis of HBV virus dynamics model with delay. Bioinformatics, 2009, 7 (4): 326- 329
doi: 10.3969/j.issn.1672-5565.2009.04.022 |
|
| 8 |
Wang K F , Fan A J , Torres A . Global properties of an improved hepatitis B virus model. Nonlinear Anal-Real, 2010, 11 (4): 3131- 3138
doi: 10.1016/j.nonrwa.2009.11.008 |
| 9 |
Xie Q Z , Huang D W , Zhang S D , et al. Analysis of a viral infection model with delayed immune response. Appl Math Model, 2010, 34 (9): 2388- 2395
doi: 10.1016/j.apm.2009.11.005 |
| 10 | Vargas-De-Leon C . Stability analysis of a model for HBV infection with cure of infected cells and intracellular delay. Appl Math Comput, 2012, 219 (1): 389- 398 |
| 11 |
Wang Y , Liu X N . Dynamical behaviors of a delayed HBV infection model with logistic hepatocyte growth, cure rate and CTL immune response. Japan J Ind Appl Math, 2015, 32 (3): 575- 593
doi: 10.1007/s13160-015-0184-6 |
| 12 |
靖晓洁, 赵爱民, 刘桂荣. 考虑部分免疫和环境传播的麻疹传染病模型的全局稳定性. 数学物理学报, 2019, 39A (1): 909- 917
doi: 10.3969/j.issn.1003-3998.2019.04.018 |
|
Jing X J , Zhao A M , Liu G R . Global stability of a measles epidemic model with partial immunity and environmental transmission. Acta Math Sci, 2019, 39A (4): 909- 917
doi: 10.3969/j.issn.1003-3998.2019.04.018 |
|
| 13 |
Dokoumetzidis A , Macheras P . Fractional kinetics in drug absorption and disposition processes. Journal of Pharmacokinetics and Pharmacodynamics, 2009, 36 (2): 165- 178
doi: 10.1007/s10928-009-9116-x |
| 14 |
Srivastava H M , Saad K M , Khader M M . An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the ebola virus. Chaos Soliton Fract, 2020, 140, 110174
doi: 10.1016/j.chaos.2020.110174 |
| 15 |
朱波, 刘立山. 带瞬时脉冲的分数阶非自制发展方程解的存在唯一性. 数学物理学报, 2019, 39A (1): 105- 113
doi: 10.3969/j.issn.1003-3998.2019.01.010 |
|
Zhu B , Liu L S . Existence and uniqueness of the mild solutions for a class of fractional non-autonomous evolution equations with impulses. Acta Math Sci, 2019, 39A (1): 105- 113
doi: 10.3969/j.issn.1003-3998.2019.01.010 |
|
| 16 |
Stanislavsky A A . Memory effects and macroscopic manifestation of randomness. Phys Rev E, 2000, 61 (5): 4752- 4759
doi: 10.1103/PhysRevE.61.4752 |
| 17 |
Vargas-De-Leon C . Volterra-type Lyapunov functions for fractional-order epidemic systems. Commun Nonlinear Sci Numer Simul, 2015, 24, 75- 85
doi: 10.1016/j.cnsns.2014.12.013 |
| 18 |
Salman S M , Yousef A M . On a fractional-order model for HBV infection with cure of infected cells. Journal of the Egyptian Mathematical Society, 2017, 25 (4): 445- 451
doi: 10.1016/j.joems.2017.06.003 |
| 19 |
Ullah S , Khan M A , Farooq M . A new fractional model for the dynamics of the hepatitis B virus using the Caputo-Fabrizio derivative. Eur Phys J Plus, 2018, 133 (6): 237
doi: 10.1140/epjp/i2018-12072-4 |
| 20 |
Ullah S , Khan M A , Farooq M . Modeling and analysis of the fractional HBV model with Atangana-Baleanu derivative. Eur Phys J Plus, 2018, 133 (8): 313
doi: 10.1140/epjp/i2018-12120-1 |
| 21 | 高飞, 胡道楠, 童恒庆, 等. 分数阶Willis环脑迟发性动脉瘤时滞系统混沌分析. 物理学报, 2018, 67 (15): 303- 313 |
| Gao F , Hu D N , Tong H Q , et al. Chaotic analysis of fractional Willis delayed aneurysm system. Acta Phys Sin, 2018, 67 (15): 303- 313 | |
| 22 |
Wang X H , Wang Z , Huang X , et al. Dynamic analysis of a delayed fractional-order SIR model with saturated incidence and treatment functions. Int J Bifurcat Chaos, 2018, 28 (14): 1850180
doi: 10.1142/S0218127418501808 |
| 23 | Podlubny I . Fractional Differential Equations. New York: Academic Press, 1999 |
| 24 | Diethelm K . The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo type. New York: Springer, 2010 |
| 25 | Huo R , Wang X L , Wu G R . Large existence and uniqueness of solutions for a class of fractional integral-differential equations with time-delay. Journal of Inner Mongolia Agricultural University(Natural Science Edition), 2014, (35): 169 |
| 26 |
Li Y , Chen Y Q , Podlubny I . Mittag-Leffler stability of fractional order nonlinear dynamic systems. Automatica, 2009, 45 (8): 1965- 1969
doi: 10.1016/j.automatica.2009.04.003 |
| 27 |
Li Y , Chen Y Q , Podlubny I . Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput Math Appl, 2010, 59 (5): 1810- 1821
doi: 10.1016/j.camwa.2009.08.019 |
| 28 |
Hu J B , Lu G P , Zhang S B , et al. Lyapunov stability theorem about fractional system without and with delay. Commun Nonlinear Sci, 2015, 20 (3): 905- 913
doi: 10.1016/j.cnsns.2014.05.013 |
| 29 |
Aguila-Camacho N , Duarte-Mermoud M A , Gallegos J A . Lyapunov functions for fractional order systems. Commun Nonlinear Sci, 2014, 19 (9): 2951- 2957
doi: 10.1016/j.cnsns.2014.01.022 |
| 30 | 张琪昌. 分岔与混沌理论及应用. 天津: 天津大学出版社, 2005 |
| Zhang Q C . Bifurcation and Chaos Theory and Its Application. Tianjin: Tianjin University Press, 2005 | |
| 31 | Cooke K L , Van Den Driessche P . On zeroes of some transcendental equations. Funkc Ekvacioj, 1986, 29 (1): 77- 90 |
| 32 | Matignon D . Stability results for fractional differential equations with applications to control processing. Computational Engineering in Systems Applications, 1996, 2, 963- 968 |
| 33 |
庄科俊. 一类时滞乙肝病毒模型的稳定性分析. 中北大学学报(自然科学版), 2015, (2): 122- 125
doi: 10.3969/j.issn.1673-3193.2015.02.006 |
|
Zhuang K J . Stability analysis for a hepatitis B virus model with time delay. Journal of North University of China(Natural Science Edition), 2015, (2): 122- 125
doi: 10.3969/j.issn.1673-3193.2015.02.006 |
|
| 34 | Van den Driessche P , Watmough J . Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci, 2002, 180 (1/2): 29- 48 |
| 35 |
Tam J . Delay effect in a model for virus replication. Math Med Bilo: A Journal of the IMA, 1999, 16 (1): 29- 37
doi: 10.1093/imammb/16.1.29 |
| 36 |
Li M Y , Shu H . Global dynamics of an in-host viral model with intracellular delay. B Math Biol, 2010, 72 (6): 1492- 1505
doi: 10.1007/s11538-010-9503-x |
| 37 | Ruan S , Wei J . On the zeros of transcendental functions with applications to stability of delay differential equations with two delays. Dynam Cont Dis Ser A, 2003, 10, 863- 874 |
| 38 | Lasalle J P . The Stability of Dynamical Systems. Philadelphia: SIMA, 1976 |
| [1] | Dandan Du,Yucan Zhu. Stabilities of K- Frames and Tight K- Frames Under the Operator Perturbation [J]. Acta mathematica scientia,Series A, 2021, 41(1): 29-38. |
| [2] | Gaihui Guo,Xiaohui Liu. Hopf Bifurcation and Stability for an Autocatalytic Reversible Biochemical Reaction Model [J]. Acta mathematica scientia,Series A, 2021, 41(1): 166-177. |
| [3] | Zerong He,Zhiqiang Zhang,Yang Wang. Stability of a Class of Nonlinear Hierarchical Age-Dependent Population Model [J]. Acta mathematica scientia,Series A, 2020, 40(6): 1712-1722. |
| [4] | Wei Li,Pengzhan Huang. A Viscosity-Splitting Finite Element Method for the Fluid-Fluid Interaction Problem [J]. Acta mathematica scientia,Series A, 2020, 40(5): 1362-1380. |
| [5] | Yonghui Zhou. Global Stability of the Nonmonotone Critical Traveling Waves for Reaction Diffusion Equations [J]. Acta mathematica scientia,Series A, 2020, 40(4): 983-992. |
| [6] | Jian Liu,Zhixin Zhang,Wei Jiang. Global Mittag-Leffler Stability of Fractional Order Nonlinear Impulsive Differential Systems with Time Delay [J]. Acta mathematica scientia,Series A, 2020, 40(4): 1053-1060. |
| [7] | Xingshou Huang,Ricai Luo,Wusheng Wang. Stability Analysis for a Class Neural Network with Proportional Delay Based on the Gronwall Integral Inequality [J]. Acta mathematica scientia,Series A, 2020, 40(3): 824-832. |
| [8] | Chun Wang,Tianzhou Xu. Hyers-Ulam-Rassias Stability of a Mixed Type Cubic-Quartic Functional Equation in 2-Banach Spaces [J]. Acta mathematica scientia,Series A, 2020, 40(2): 352-368. |
| [9] | Cheng Ouyang,Weigang Wang,Jiaqi Mo. The Fractional Generalized Disturbed Thermal Wave Equation [J]. Acta mathematica scientia,Series A, 2020, 40(2): 452-459. |
| [10] | Menglan Liao,Bin Guo. Asymptotic Stability of Weak Solutions to Wave Equation with Variable Exponents and Strong Damping Term [J]. Acta mathematica scientia,Series A, 2020, 40(1): 146-155. |
| [11] | Ru Wang,Zhonghua Zhang,Yeling Liu. Dynamical Properties of a Discontinuous Models with Signal Molecules Regulation [J]. Acta mathematica scientia,Series A, 2019, 39(6): 1545-1554. |
| [12] | Chao Yang,Runjie Li. Existence and Stability of Periodic Solution for a Lasota-Wazewska Model with Discontinuous Harvesting [J]. Acta mathematica scientia,Series A, 2019, 39(4): 785-796. |
| [13] | Qinghua Zhou,Li Wan,Jie Liu. Global Attracting Set for Neutral Type Hopfield Neural Networks with Time-Varying Delays [J]. Acta mathematica scientia,Series A, 2019, 39(4): 823-831. |
| [14] | Yanhua Shi,Yadong Zhang,Fenling Wang,Yanmin Zhao,Pingli Wang. High Accuracy Analysis of Linear Triangular Element for Time Fractional Diffusion Equations [J]. Acta mathematica scientia,Series A, 2019, 39(4): 839-850. |
| [15] | Changxu Shao,Shutang Liu. Fractal Feature and Control of Three-Species Predator-Prey Model [J]. Acta mathematica scientia,Series A, 2019, 39(4): 951-962. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 140
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 105
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|