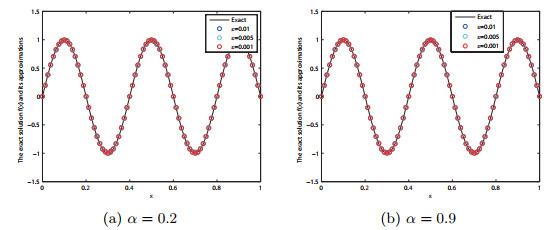
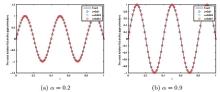
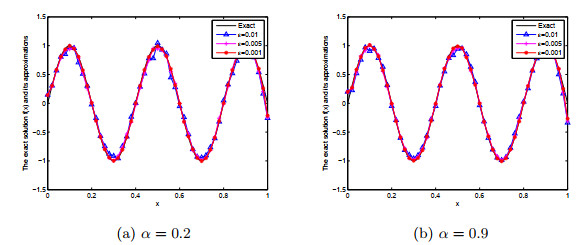
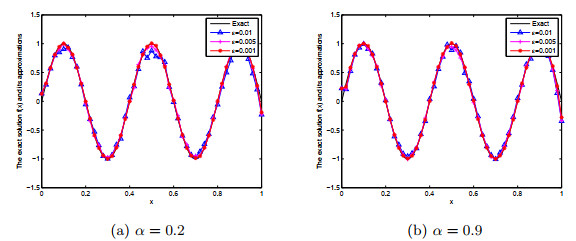
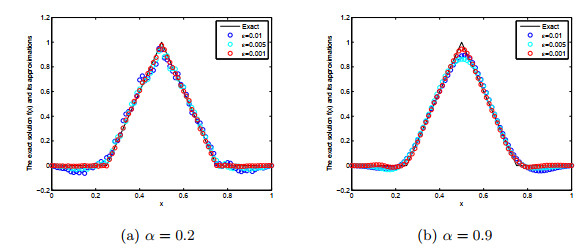
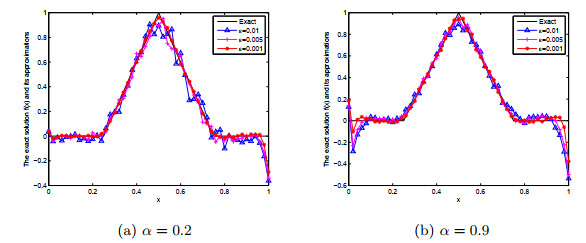
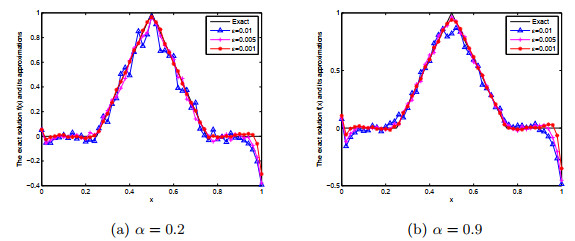
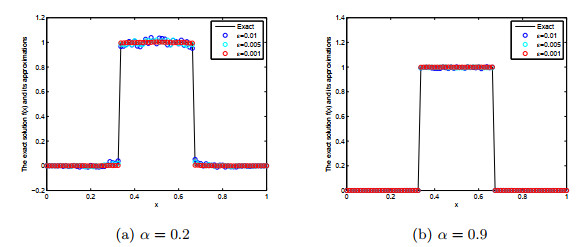
Acta mathematica scientia,Series A ›› 2021, Vol. 41 ›› Issue (2): 427-450.
Previous Articles Next Articles
Fractional Landweber Iterative Regularization Method to Identify Source Term for the Rayleigh-Stokes Equation
Fan Yang*( ),Qianchao Wang(
),Qianchao Wang( ),Xiaoxiao Li
),Xiaoxiao Li
- School of Science, Lanzhou University of Technology, Lanzhou 730050
-
Received:2020-03-03Online:2021-04-26Published:2021-04-29 -
Contact:Fan Yang E-mail:yfggd114@163.com;wqcfaf@163.com -
Supported by:the NSFC(11961044);the Dr Fund of Lanzhou University of Science and Technology
CLC Number:
- O175
Cite this article
Fan Yang,Qianchao Wang,Xiaoxiao Li. Fractional Landweber Iterative Regularization Method to Identify Source Term for the Rayleigh-Stokes Equation[J].Acta mathematica scientia,Series A, 2021, 41(2): 427-450.
share this article
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| η(f) | ε=0.01 | Landweber | BD | 0.0099 | 0.0083 | 0.0075 |
| C-N | 0.0072 | 0.0052 | 0.0041 | |||
| 分数阶Landweber | BD | 0.0088 | 0.0076 | 0.0061 | ||
| C-N | 0.0063 | 0.0048 | 0.0039 | |||
| ε=0.005 | Landweber | BD | 0.0042 | 0.0039 | 0.0034 | |
| C-N | 0.0041 | 0.0035 | 0.0025 | |||
| 分数阶Landweber | BD | 0.0038 | 0.0035 | 0.0021 | ||
| C-N | 0.0031 | 0.0028 | 0.0011 | |||
| ε= 0.001 | Landweber | BD | 0.0025 | 0.0019 | 7.9678e-04 | |
| C-N | 0.0020 | 0.0011 | 5.5690e-04 | |||
| 分数阶Landweber | BD | 0.0018 | 0.0010 | 7.1943e-04 | ||
| C-N | 0.0011 | 8.7631e-04 | 4.6982e-04 | |||
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| 迭代步数(m) | ε = 0.01 | Landweber | BD | 24027 | 9658 | 30 |
| C-N | 25556 | 31634 | 37652 | |||
| 分数阶Landweber | BD | 19683 | 6514 | 21 | ||
| C-N | 21423 | 23963 | 29685 | |||
| ε = 0.005 | Landweber | BD | 46820 | 21349 | 34 | |
| C-N | 27941 | 30652 | 39541 | |||
| 分数阶Landweber | BD | 39870 | 12981 | 29 | ||
| C-N | 19685 | 23916 | 33921 | |||
| ε = 0.001 | Landweber | BD | 79686 | 38679 | 44 | |
| C-N | 35719 | 42387 | 52802 | |||
| 分数阶Landweber | BD | 68765 | 27695 | 38 | ||
| C-N | 26985 | 34796 | 44348 | |||
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| CPU时间(unit: s) | ε = 0.01 | Landweber | BD | 480.54 | 193.16 | 0.60 |
| C-N | 511.12 | 632.68 | 753.04 | |||
| 分数阶Landweber | BD | 393.66 | 130.28 | 0.42 | ||
| C-N | 428.46 | 479.26 | 593.70 | |||
| ε = 0.005 | Landweber | BD | 936.40 | 426.98 | 0.68 | |
| C-N | 558.82 | 613.04 | 790.82 | |||
| 分数阶Landweber | BD | 797.40 | 259.62 | 0.58 | ||
| C-N | 393.70 | 478.32 | 678.42 | |||
| ε = 0.001 | Landweber | BD | 1593.72 | 773.58 | 0.88 | |
| C-N | 714.38 | 847.74 | 1056.04 | |||
| 分数阶Landweber | BD | 1375.30 | 553.90 | 0.76 | ||
| C-N | 539.70 | 695.92 | 886.96 | |||
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| η(f) | ε = 0.01 | Landweber | BD | 0.0243 | 0.0128 | 0.0088 |
| C-N | 0.1039 | 0.0864 | 0.0747 | |||
| 分数阶Landweber | BD | 0.0208 | 0.0106 | 0.0075 | ||
| C-N | 0.0931 | 0.0705 | 0.0628 | |||
| ε = 0.005 | Landweber | BD | 0.0155 | 0.0116 | 0.0076 | |
| C-N | 0.0838 | 0.0725 | 0.0634 | |||
| 分数阶Landweber | BD | 0.0191 | 0.0103 | 0.0063 | ||
| C-N | 0.0786 | 0.0596 | 0.0413 | |||
| ε = 0.001 | Landweber | BD | 0.0033 | 0.0019 | 8.6476e-04 | |
| C-N | 0.0589 | 0.0362 | 0.0295 | |||
| 分数阶Landweber | BD | 0.0021 | 0.0011 | 6.5483e-04 | ||
| C-N | 0.0412 | 0.0268 | 0.0105 | |||
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| 迭代步数(m) | ε = 0.01 | Landweber | BD | 22348 | 6987 | 29 |
| C-N | 3717 | 5816 | 7425 | |||
| 分数阶Landweber | BD | 16534 | 3768 | 19 | ||
| C-N | 2674 | 4168 | 6123 | |||
| ε = 0.005 | Landweber | BD | 34258 | 12368 | 33 | |
| C-N | 6670 | 8126 | 11198 | |||
| 分数阶Landweber | BD | 22369 | 6879 | 26 | ||
| C-N | 4396 | 6021 | 8934 | |||
| ε = 0.001 | Landweber | BD | 79463 | 39654 | 41 | |
| C-N | 15285 | 86956 | 131965 | |||
| 分数阶Landweber | BD | 54986 | 21685 | 33 | ||
| C-N | 13210 | 69663 | 113824 | |||
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| CPU时间(unit: s) | ε = 0.01 | Landweber | BD | 446.96 | 139.74 | 0.58 |
| C-N | 74.34 | 116.32 | 148.50 | |||
| 分数阶Landweber | BD | 330.68 | 75.36 | 0.38 | ||
| C-N | 53.48 | 83.36 | 122.46 | |||
| ε = 0.005 | Landweber | BD | 685.16 | 247.36 | 0.66 | |
| C-N | 133.4 | 162.52 | 223.96 | |||
| 分数阶Landweber | BD | 447.38 | 137.58 | 0.52 | ||
| C-N | 87.92 | 120.42 | 178.68 | |||
| ε = 0.001 | Landweber | BD | 1589.26 | 793.08 | 0.82 | |
| C-N | 305.70 | 1739.12 | 2639.3 | |||
| 分数阶Landweber | BD | 1099.72 | 433.70 | 0.66 | ||
| C-N | 264.20 | 1393.26 | 2276.48 | |||
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| η(f) | ε = 0.01 | Landweber | BD | 0.0287 | 0.0196 | 0.0100 |
| C-N | 0.1867 | 0.2375 | 0.2735 | |||
| 分数阶Landweber | BD | 0.0234 | 0.0165 | 0.0008 | ||
| C-N | 0.1529 | 0.2143 | 0.2568 | |||
| ε = 0.005 | Landweber | BD | 0.0176 | 0.0102 | 0.0050 | |
| C-N | 0.1679 | 0.2139 | 0.2228 | |||
| 分数阶Landweber | BD | 0.0153 | 0.0088 | 0.0016 | ||
| C-N | 0.1428 | 0.1796 | 0.1928 | |||
| ε = 0.001 | Landweber | BD | 0.0068 | 0.0036 | 0.0010 | |
| C-N | 0.0924 | 0.1428 | 0.1522 | |||
| 分数阶Landweber | BD | 0.0053 | 0.0018 | 2.5638e-04 | ||
| C-N | 0.0723 | 0.1256 | 0.1347 | |||
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| 迭代步数(m) | ε = 0.01 | Landweber | BD | 47906 | 21398 | 29 |
| C-N | 4837 | 8878 | 19844 | |||
| 分数阶Landweber | BD | 31695 | 10321 | 18 | ||
| C-N | 2968 | 5367 | 16482 | |||
| ε = 0.005 | Landweber | BD | 74840 | 46709 | 33 | |
| C-N | 10244 | 168704 | 52632 | |||
| 分数阶Landweber | BD | 62390 | 30987 | 28 | ||
| C-N | 7688 | 11326 | 40986 | |||
| ε = 0.001 | Landweber | BD | 121803 | 76895 | 42 | |
| C-N | 238323 | 638825 | 788528 | |||
| 分数阶Landweber | BD | 98465 | 54326 | 37 | ||
| C-N | 196524 | 419168 | 568238 | |||
"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| CPU时间(unit: s) | ε = 0.01 | Landweber | BD | 958.12 | 427.96 | 0.58 |
| C-N | 96.74 | 177.56 | 396.88 | |||
| 分数阶Landweber | BD | 639.30 | 206.42 | 0.36 | ||
| C-N | 59.36 | 107.34 | 329.64 | |||
| ε = 0.005 | Landweber | BD | 1496.80 | 934.18 | 0.66 | |
| C-N | 204.88 | 3374.08 | 1052.64 | |||
| 分数阶Landweber | BD | 1247.80 | 619.74 | 0.56 | ||
| C-N | 153.76 | 226.52 | 819.72 | |||
| ε = 0.001 | Landweber | BD | 2436.06 | 1537.90 | 0.84 | |
| C-N | 4766.46 | 12776.50 | 15770.56 | |||
| 分数阶Landweber | BD | 1969.30 | 1086.52 | 0.74 | ||
| C-N | 3930.48 | 8383.36 | 11364.76 | |||
| 1 |
Fetecau C . The Rayleigh-Stokes problem for heated second grade fluids. Int J Nonlin Mech, 2002, 37, 1011- 1015
doi: 10.1016/S0020-7462(00)00118-9 |
| 2 |
Shen F , Tan W , Zhao Y , et al. The Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative model. Nonlinear Anal Real World Appl, 2006, 7, 1072- 1080
doi: 10.1016/j.nonrwa.2005.09.007 |
| 3 |
Khan M , Anjum A , Qi H , et al. On exact solutions for some oscillating motions of a generalized Oldroyd-B fluid. Z Angew Math Phys, 2010, 61, 133- 145
doi: 10.1007/s00033-009-0004-4 |
| 4 |
Khan M . The Rayleigh-Stokes problem for an edge in a viscoelastic fluid with a fractional derivative model. Nonlinear Anal Real Word Appl, 2009, 10, 3190- 3195
doi: 10.1016/j.nonrwa.2008.10.002 |
| 5 | Chen C M , Liu F , Burrage K , et al. Numerical methods of the variable-order Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative. J Appl Math, 2013, 204, 340- 351 |
| 6 |
Yu B , Jiang X Y , Qi H T . An inverse problem to estimate an unknown order of a Riemann-Liouville fractional derivative for a fractional Stokes' first problem for a heated generalized second grade fluid. Acta Mechanica Sinica, 2015, 31, 153- 161
doi: 10.1007/s10409-015-0408-7 |
| 7 | Zhuang P H , Liu Q X . Numerical method of Rayleigh-Stokes problem for heated generalized second grade fluid with fractional derivative. Appl Math Model, 2009, 30, 1533- 1546 |
| 8 |
Chen C M , Liu F , Burrage K , et al. Numerical methods with fourth-order spatial accuracy for variable-order nonlinear Stokes' first problem for a heated generalized second grade fluid. Comput Math Appl, 2011, 62, 971- 986
doi: 10.1016/j.camwa.2011.03.065 |
| 9 |
Wu C . Numerical solution for Stokes' first problem for a heated generalized second grade fluid with fractional derivative. Appl Numer Math, 2009, 59, 2571- 2583
doi: 10.1016/j.apnum.2009.05.009 |
| 10 |
Mohebbi A , Abbaszadeh M , Dehghan M . Compact finite difference scheme and RBF meshless approach for solving 2D Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives. Comput Methods Appl Mech Eng, 2013, 264, 163- 177
doi: 10.1016/j.cma.2013.05.012 |
| 11 |
Dehghan M , Safarpoor M , Abbaszadeh M . Two high-order numerical algorithms for solving the multi-term time fractional diffusion-wave equations. J Comput Appl Math, 2015, 290, 174- 195
doi: 10.1016/j.cam.2015.04.037 |
| 12 |
Dehghan M , Abbaszadeh M , Deng W . Fourth-order numerical method for the space time tempered fractional diffusion-wave equation. Appl Math Lett, 2017, 73, 120- 127
doi: 10.1016/j.aml.2017.04.011 |
| 13 |
Mirzaei D , Dehghan M . New implementation of MLBIE method for heat conduction analysis in functionally graded materials. Eng Anal Bound Elem, 2012, 36, 511- 519
doi: 10.1016/j.enganabound.2011.11.007 |
| 14 |
Mohebbi A , Abbaszadeh M , Dehghan M . Compact finite difference scheme and RBF meshless approach for solving 2D Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives. Comput Methcd Appl M, 2013, 264, 163- 177
doi: 10.1016/j.cma.2013.05.012 |
| 15 | Nguyen H L , Nguyen H T , Mokhtar K . Identifying initial condition of the Rayleigh-Stokes problem with random noise. Math Method Appl Sci, 2019, |
| 16 | Nguyen A L , Hoan Luu V C , Nguyen H L . Identification of source term for the Rayleigh-Stokes problem with Gaussian random noise. Math Method Appl Sci, 2018, |
| 17 |
Dehghan M . An inverse problem of finding a source parameter in a semilinear parabolic equation. Appl Math Model, 2001, 25, 743- 754
doi: 10.1016/S0307-904X(01)00010-5 |
| 18 |
Wang J , Wei T , Zhou Y . Optimal error bound and simplified Tikhonov regularization method for a backward problem for the time-fractional diffusion equation. J Comput Appl Math, 2015, 279, 277- 292
doi: 10.1016/j.cam.2014.11.026 |
| 19 |
Yang F , Li X X , Li D G , et al. The simplified Tikhonov regularization method for solving a Riesz-Feller Space-Fractional backward diffusion problem. Math Comput Sci, 2017, 11, 91- 110
doi: 10.1007/s11786-017-0292-6 |
| 20 |
Wang J G , Wei T , Zhou Y B . Tikhonov regularization method for a backward problem for the time-fractional diffusion equation. Appl Math Model, 2013, 37, 8518- 8532
doi: 10.1016/j.apm.2013.03.071 |
| 21 |
Yang F , Zhang P , Li X X , et al. Tikhonov regularization method for identifying the space-dependent source for time-fractional diffusion equation on a columnar symmetric domain. Adv Differ Equ, 2020,
doi: 10.1186/s13662-020-2542-1 |
| 22 |
Feng L X , Eldén L . Solving a Cauchy problem for a 3D elliptic PDE with variable coefficients by a quasi-boundary-value method. Inverse Probl, 2014, 30, 015005
doi: 10.1088/0266-5611/30/1/015005 |
| 23 |
Wei T , Wang J . A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation. Appl Numer Math, 2014, 78, 95- 111
doi: 10.1016/j.apnum.2013.12.002 |
| 24 |
Yang F , Sun Y R , Li X X , et al. , The quasi-boundary regularization value method for identifying the initial value of heat equation on a columnar symmetric domain. Numer Algor, 2019, 82, 623- 639
doi: 10.1007/s11075-018-0617-9 |
| 25 |
Yang F , Zhang Y , Liu X , Li X X . The quasi-boundary value method for identifying the initial value of the space-time an fractional diffusion equation. Acta Math Sci, 2020, 40, 641- 658
doi: 10.1007/s10473-020-0304-5 |
| 26 |
Qian A , Xiong X T , Wu Y . On a quasi-reversibility regularization method for a Cauchy problem of the Helmholtz equation. J Comput Appl Math, 2010, 233, 1969- 1979
doi: 10.1016/j.cam.2009.09.031 |
| 27 |
Yang F , Fu C L . The quasi-reversibility regularization method for identifying the unknown source for time fractional diffusion equation. Appl Math Model, 2015, 39, 1500- 1512
doi: 10.1016/j.apm.2014.08.010 |
| 28 |
Yang F , Fu J L , Li X X . A potential-free field inverse schrödinger problem: optimal error bound analysis and regularization method. Inverse Probl Sci Engin, 2020, 28, 1209- 1252
doi: 10.1080/17415977.2019.1700243 |
| 29 | Yang F , Fu J L , Li X X . A potential-free field inverse time-fractional Schrödinger problem: Optimal error bound analysis and regularization method. Math Meth Appl Sci, 2020, |
| 30 | Yang F , Fu C L , Li X X . A mollification regularization method for unknown source in time-fractional diffusion equation. Int J Comput Math, 2006, 91, 1516- 1534 |
| 31 |
Xiong X T , Fu C L , Li H F . Fourier regularization method of a sideways heat equation for determining surface heat flux. Math Anal Appl, 2006, 317, 331- 348
doi: 10.1016/j.jmaa.2005.12.010 |
| 32 |
Li X X , Lei J L , Yang F . An a posteriori Fourier regularization method for identifying the unknown source of the space-fractional diffusion equation. Inequal Appl, 2004, 2014, 1- 13
doi: 10.1186/1029-242X-2014-434 |
| 33 | Yang F , Fu C L , Li X X , et al. The Fourier regularization method for identifying the unknown source for the modified Helmholtz equation. Acta Math Sci, 2014, 34, 1040- 1047 |
| 34 |
Yang F , Ren Y P , Li X X . Landweber iteration regularization method for identifying unknown source on a columnar symmetric domain. Inverse Probl Sci Eng, 2018, 26, 1109- 1129
doi: 10.1080/17415977.2017.1384825 |
| 35 |
Yang F , Liu X , Li X X . Landweber iteration regularization method for identifying unknown source of the modified Helmholtz equation. Bound Value Probl, 2017, 2017, 1- 16
doi: 10.1186/s13661-016-0733-1 |
| 36 |
Yang F , Zhang Y , Li X X . Landweber iterative method for identifying the initial value problem of the time-space fractional diffusion-wave equation. Numer Algor, 2020, 83, 1509- 1530
doi: 10.1007/s11075-019-00734-6 |
| 37 | Yang F , Wang N , Li X X . Landweber iterative method for an inverse source problem of time-fractional diffusion-wave equation onspherically symmetric domain. J Appl Ana Comput, 2020, 10, 514- 529 |
| 38 |
Yang F , Zhang Y , Li X X , Ma C Y . Landweber iteration regularization method for identifying the initial value problem of the time-space fractional diffusion-wave equation. Advances in Difference Equations, 2017,
doi: 10.1007/s11075-019-00734-6 |
| 39 |
Yang F , Pu Q , Li X X . The fractional Landweber method for identifying the space source term problem for time-space fractional diffusion equation. Numer Algor, 2020,
doi: 10.1007/s11075-020-01006-4 |
| 40 |
Klann E , Maass P , Ramlau R . Two-step regularization methods for linear inverse problems. Inverse Ill-posed Probl, 2006, 14, 583- 607
doi: 10.1515/156939406778474523 |
| 41 |
Klann E , Ramlau R . Regularization by fractional filter methods and data smoothing. Inverse Probl, 2008, 24, 025018
doi: 10.1088/0266-5611/24/2/025018 |
| 42 |
Bazhlekova E , Jin B , Lazarov R , et al. An analysis of the Rayleigh-Stokes problem for a generalized second-grade fluid. Number Math, 2015, 131, 1- 31
doi: 10.1007/s00211-014-0685-2 |
| 43 | Engl H W , Hanke M , Neubauer A . Regularization of Inverse Problem. Boston: MA, Kluwer Academic, 1996 |
| 44 | Dehghan M , Abbaszadeh M . A finite element method for the numerical solution of Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives. Eng Comput-Germany, 2017, 33, 587- 605 |
| 45 |
Yuste S B . Weighted average finite difference methods for fractional diffusion equations. J Comput Phys, 2006, 216, 264- 274
doi: 10.1016/j.jcp.2005.12.006 |
| 46 |
Irene K . A posteriori error analysis for the Crank-Nicolson method for linear Schrödinger equations. Esaim-Math Model Num, 2011, 45, 761- 778
doi: 10.1051/m2an/2010101 |
| [1] | WANG Yu-Ping. Inverse Problem for Diffusion Operators from Interior Spectral Data [J]. Acta mathematica scientia,Series A, 2013, 33(6): 1189-1195. |
| [2] | WANG Yu-Ping. A Uniqueness Theorem for Diffusion Operators on the Finite Interval [J]. Acta mathematica scientia,Series A, 2013, 33(2): 333-339. |
| [3] | Wang-Yu-Hua, WEI Guang-Sheng. The Uniqueness for Inverse Sturm-Liouville Problems with Aftereffect [J]. Acta mathematica scientia,Series A, 2012, 32(6): 1171-1178. |
| [4] | WEI Ying, DAI Hua. Construction of Jacobi Matrix from its Submatrix and Spectrum and |its Expansion [J]. Acta mathematica scientia,Series A, 2012, 32(2): 356-363. |
| [5] | DOU Yi-Xin, HAN Bo. A Nonlinear Multigrid-FEM Inversion Algorithm for Reconstruction of a Mountain Surface [J]. Acta mathematica scientia,Series A, 2011, 31(6): 1479-1489. |
| [6] | WANG Wu-Ping, YANG Chuan-Fu, HUANG Zhen-You. Half Inverse Problem for a Quadratic Pencil of |Schr\"{o}dinger Operators [J]. Acta mathematica scientia,Series A, 2011, 31(6): 1708-1717. |
| [7] | MO Rong-Hua, LI Wen. The Inverse Eigenvalue Problem of Hermitian and Generalized Skew-Hamiltonian |Matrices with a Submatrix Constraint and Its Approximation [J]. Acta mathematica scientia,Series A, 2011, 31(3): 691-701. |
| [8] | YUAN Yong-Xin, DAI Hua. Inverse Problems for Generalized Reflexive Matrices on a Linear Manifold [J]. Acta mathematica scientia,Series A, 2009, 29(6): 1547-1560. |
| [9] | TAO You-Shan, BIAN Bao-Jun. Parameter Identification for a Model of Tumor Growth in the Presence of Inhibitors [J]. Acta mathematica scientia,Series A, 2009, 29(5): 1175-1186. |
| [10] | Gong Lisha; Hu Xiyan; Zhang Lei. The Inverse Problem of Hermitian-Hamiltonian Matrices with a Submatrix Constraint [J]. Acta mathematica scientia,Series A, 2008, 28(4): 694-700. |
| [11] | Hao Xin-sheng. An Inverse |problem of |a Semilinear Wave Equation [J]. Acta mathematica scientia,Series A, 2000, 20(zk): 602-609. |
| [12] | Zhang Yi | Mei Fengxiang. Lie Symmetries and Conserved Quantities of Nonholonomic Mechanical Systems with Unilateral Constraints [J]. Acta mathematica scientia,Series A, 2000, 20(1): 95-100. |
| [13] | Liu Jijun, Wang Yuanming. Appromaxlmation and Convergence of a Class of Hyperbolic Inverse Problem [J]. Acta mathematica scientia,Series A, 1997, 17(2): 134-144. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 114
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 87
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|