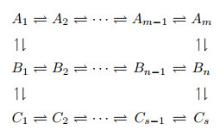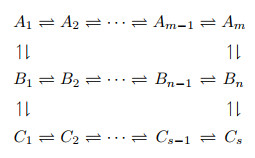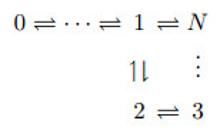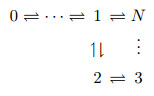有环的可逆马氏链的统计确认

Abstract

Abstract:

The statistical identification of Markov chain explores how to identify the transition rate matrix of the underlying Markov chain by partially observable data. SIMC on reversibly cyclic graphs (containing one cycle at least), as the most important and crucial class, is investigated then in this letter. As the differentials of hitting time distribution for a reversible Markov chain are expressed by taboo rates, the necessary condition is developed to identify the transition rate matrix and a general conclusion about sufficiency is provided. The proposed algorithms to exactly calculate all transition rates are developed. A numerical example is included to demonstrate the correctness of the proposed algorithms.

Key words: Reversible Markov chain, Transition rate matrix, Statistical identification, Cyclic graph, Hitting time

CLC Number:

O211.62

Xuyan Xiang,Haiqin Fu,Jieming Zhou,Yingchun Deng,Xiangqun Yang. Statistical Identification of Reversible Markov Chain on Cyclic Graph[J].Acta mathematica scientia,Series A, 2020, 40(6): 1682-1698.

Trendmd

Figures/Tables 6

References 33

1	Albrecher H , Boxma O . On the discounted penalty function in a Markov-dependent risk model. Insurance:Mathematics and Economics, 2005, 37 (3): 650- 672
2	Amann C , Schmiedl T . Communications:can one identify nonequilibrium in a three-state system by analyzing two-state trajectories?. J Chem Phys, 2010, 132: 041102
3	Ball F , Milne R . Marked continuous-time markov chain modelling of burst behaviour for single ion channels. J Appl Math Deci Sci, 2007, 11: 48138- 48151
4	Chen M. From Markov Chains To Non-Equilibrium Particle Systems. Singapore: World Scientific, 2004
5	Colquhoun D . On the stochastic properties of bursts of single ion channels opening and of clusters of brusts. Philos Trans R Soc Lond Biol Sci, 1982, 300: 1- 59
6	Colquhoun D , Hatton C , Hawkes A . The quality of maximum likelihood estimates of ion channel rate constants. J Physiol, 2003, 547: 699- 728
7	Coolen-Schrijner P . The deviation matrix of a continuous-time Markov chain. Probability in the Engineering and Informational Sciences, 2002, 16: 351- 366
8	De La Pena V , Gzyl H , Mcdonald P . Hitting time and inverse problems for Markov chains. Journal of Applied Probability, 2008, 45 (3): 640- 649
9	Deng Y , Peng S , Qian M , Feng J . Identifying transition rates of ionic channel via observation of a single state. J Phys A Math Gen, 2003, 36: 1195- 1212
10	Elliot R, Aggoun L, Moore J. Hidden Markov Models: Estimation and Control. New York: Springer-Verlag, 1995
11	Flomenbom O , Silbey R . Utilizing the information content in two-state trajectories. Proc Natl Acad Sci, 2006, 103: 10907- 10910
12	Flomenbom O , Silbey R . Toolbox for analyzing finite two-state trajectories. Phys Rev E, 2008, 78: 066105
13	Fredkin D , Rice J . On aggregated Markov processes. Journal of Applied Probability, 1986, 23: 208- 214
14	French R , Wonderlin W . Software for acquisition and analysis of ion channel data:choices, tasks, and strategies. Methods Enzymol, 1992, 207: 711- 728
15	侯振挺. Q过程的唯一性准则. 长沙: 湖南科学技术出版社, 1982
	Hou Z T . Uniqueness Criterion of Q Process. Changsha: Hunan Science and Technology Press, 1982
16	Horn R , Lang K . Estimating kinetic constants from single channel data. Biophys, 1983, 43: 207- 230
17	Jewell N. Mixtures of exponential distributions. Ann Statist 1982, 10: 479-484
18	Jia C , Chen Y . A second perspective on the Amann-Schmiedl-Seifert criterion for nonequilibrium in a three-state system. J Phys A:Math Theor, 2015, 48: 205001
19	Keatinge C . Modelling losses with the mixed exponential distribution. Proceeding of the Causality Actuarial Society, 1999, 86: 654- 698
20	Kelly F. Reversibility and Stochastic Networks. New York: John Wiley, 1979
21	Larget B . A canonical representation for aggregated Markov processes. J Appl Prob, 1998, 35: 313- 324
22	钱敏平, 龚光鲁. 随机过程论(第二版). 北京: 北京大学出版社, 1997
	Qian M P , Gong G L . Stochastic Process Theory (Second Edition). Beijing: Beijing University Press, 1997
23	Sakemann B, Neher E. Single-Channel Recording. New York: Springer, 2009
24	Shelley C , Magleby K . Linking exponential components to kinetic states in markov models for single-channel gating. J Gen Physiol, 2008, 132: 295- 312
25	Wagner M , Michalek S , Timmer J . Estimating transition rates in aggregated Markov models of ion channel gating with loops and with nearly equal dwell times. Proc R Soc Lond B, 1999, 266: 1919- 1926
26	王子坤, 杨向群. 生灭过程及马尔可夫链(第二版). 北京: 科学出版社, 2005
	Wang Z K , Yang X Q . Birth and Death Process and Markov Chain (Second Edition). Beijing: Science Press, 2005
27	Xiang X , Yang X , Deng Y , Feng J . Identifying transition rates of ionic channel of star-graph branch type. J Phys A Math Gen, 2006, 39: 9477- 9491
28	Xiang X , Deng Y , Yang X . Markov chain inversion approach to identify the transition rates of ion channels. Acta Mathematica Scientia, 2012, 32
29	Xiang X , Fu H , Zhou J , et al. Taboo rate and hitting time distribution of continuous-time reversible Markov chains. Statistics & Probability Letters, 2021, 169: 108969
30	向绪言, 杨向群, 邓迎春. 确定一类带环离子通道门控的转移速率. 高校应用数学学报, 2009, 24 (2): 146- 154
	Xiang X , Yang X , Deng Y . Identifying transition rates for a type of gating schemes of ion channels with loops. Appl Math A Journal Chinese Univ, 2009, 24 (2): 146- 154
31	向绪言, 杨向群, 邓迎春. 确定环形Markov链的Q-矩阵. 数学学报, 2013, 56 (5): 735- 749
	Xiang X , Yang X , Deng Y . Identifying Q-matrix of cyclic Markov chain. Acta Mathematica Sinica, 2013, 56 (5): 735- 749
32	Xiang X , Zhang X , Mo X . Statistical identification of Markov chain on trees. Mathematical Problems in Engineering, 2018, (4): 1- 13 doi: 10.1155/2036248
33	杨向群. 可列马尔可夫过程构造论(第二版). 长沙: 湖南科技出版社, 1986
	Yang X Q . On the Construction of Countable Markov Processes (Second Edition). Changsha: Hunan Science and Technology Press, 1986

Statistical Identification of Reversible Markov Chain on Cyclic Graph

RichHTML

PDF (PC)

Abstract

Cite this article

share this article

Figures/Tables 6

References 33

Related Articles 1

Metrics

Comments

Recommended 10