次临界 Choquard 方程的多解

摘要/Abstract

摘要：

该文考虑次临界 Choquard 方程

{\begin{cases} - Δ u + (λ V (x) + 1) u = (\int_{R^{N}} \frac{| u (y) |^{p_{ε}}}{| x - y |^{μ}} d y) | u |^{p_{ε} - 2} u, x \in R^{N}, \\ u \in H^{1} (R^{N}) \end{cases}

$\begin{cases} -{\Delta}{u}+(\lambda V(x)+1)u=\Big(\int_{\mathbb{R}^N} \frac{|u(y)|^{p_{\varepsilon}}}{|x-y|^\mu} {\rm d}y\Big)|u|^{p_{\varepsilon}-2}u,\quad x\in\mathbb{R}^N,\\{u\in{{H}}^{1}{(\mathbb{R}^N)}} \end{cases}$ (0.1)

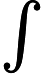
多解的存在性, 其中 $N>3$ , $\lambda$ 是正实参数, $p_{\varepsilon}=2^\ast_{\mu}-\varepsilon$ , $\varepsilon>0$ , $0<\mu<N$ , $2^\ast_{\mu}=\frac{2N-\mu}{N-2}$ 是 Hardy-Littlewood-Sobolev 不等式意义下的临界指数. 假定 $\Omega:={\rm int}\,V^{-1}(0)$ 是 $\mathbb{R}^N$ 中非空带光滑边界的有界区域, 利用 Lusternik-Schnirelman 定理,该文证明了当 $\lambda$ 足够大及 $\varepsilon$ 充分小时, 方程(0.1)至少有 $cat_\Omega(\Omega)$ 个正解.

关键词: 次临界 Choquard 方程, Lusternik-Schnirelman 定理, 解的多重性

Abstract:

In this paper, we are concerned with the multiplicity of solutions for the following subcritical Choquard equation

{\begin{cases} - Δ u + (λ V (x) + 1) u = (\int_{R^{N}} \frac{| u (y) |^{p_{ε}}}{| x - y |^{μ}} d y) | u |^{p_{ε} - 2} u, x \in R^{N}, \\ u \in H^{1} (R^{N}), \end{cases}

$\begin{equation*} \begin{cases} -{\Delta}{u}+(\lambda V(x)+1)u=\Big(\int_{\mathbb{R}^N}\frac{|u(y)|^{p_{\varepsilon}}}{|x-y|^\mu}{\rm d}y\Big)|u|^{p_{\varepsilon}-2}u,\quad x\in\mathbb{R}^N,\\{u\in{{H}}^{1}{(\mathbb{R}^N)}}, \end{cases}\end{equation*}$

where $N>3$ , $\lambda$ is a real parameter, $p_{\varepsilon}=2^\ast_{\mu}-\varepsilon$ , $\varepsilon>0$ , $\mu\in(0,N)$ and $2^\ast_{\mu}=\frac{2N-\mu}{N-2}$ is the critical Hardy-Littlewood-Sobolev exponent. Suppose that $\Omega:={\rm int}\,V^{-1}(0)$ is a nonempty bounded domain in $\mathbb{R}^N$ with smooth boundary, using Lusternik-Schnirelman theory, we prove the problem (0.1) has at least $cat_\Omega(\Omega)$ positive solutions for $\lambda$ large and $\varepsilon$ small enough.

Key words: Subcritical Choquard equation, Lusternik-Schnirelman theory, Multiplicity of solutions

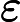
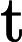
中图分类号:

O175.25

温瑞江, 刘范琴, 徐子怡. 次临界 Choquard 方程的多解[J]. 数学物理学报, 2024, 44(1): 60-79.

Wen Ruijiang, Liu Fanqin, Xu Ziyi. Multiplicity of Positive Solutions to Subcritical Choquard Equation[J]. Acta mathematica scientia,Series A, 2024, 44(1): 60-79.

参考文献 31

[1]	Alves C O, Nóbrega A B, Yang M B. Multi-bump solutions for Choquard equation with deepening potential well. Calc Var Partial Differ Equ, 2016, 55(3): 1-28 doi: 10.1007/s00526-015-0942-y
[2]	Alves C O, Barros L M. Existence and multiplicity of solutions for a class of elliptic problem with critical growth. Monatsh Math, 2018, 187(2): 195-215 doi: 10.1007/s00605-017-1117-z
[3]	Ambrosetti A, Brezis H, Cerami G. Combined effects of concave and convex nonlinearities in some elliptic problems. J Funct Anal, 1994, 122(2): 519-543 doi: 10.1006/jfan.1994.1078
[4]	Alves C O, Ding Y H. Multiplicity of positive solutions to a $p$ -Laplacian equation involving critical nonlinearity. J Math Anal Appl, 2003, 279(2): 508-521 doi: 10.1016/S0022-247X(03)00026-X
[5]	Bahri A, Coron J M. On a nonlinear elliptic equation involving the Sobolev exponent: The effect of the topology of the domain. Comm Pure Appl Math, 1988, 41(3): 253-294 doi: 10.1002/cpa.v41:3
[6]	Bartsch T, Wang Z Q. Multiple positive solutions for a nonlinear Schrödinger equation. Z Angew Math Phys, 2000, 51(3): 366-384 doi: 10.1007/PL00001511
[7]	Benci V, Cerami G. Positive solutions of some nonlinear elliptic problems in exterior domains. Arch Rational Mech Anal, 1987, 99(4): 283-300 doi: 10.1007/BF00282048
[8]	Benci V, Cerami G. The effect of the domain topology on the number of positive solutions of nonlinear elliptic problems. Arch Rational Mech Anal, 1991, 114(1): 79-93 doi: 10.1007/BF00375686
[9]	Benci V, Cerami G. Multiple positive solutions of some elliptic problems via the Morse theorem and the domain topology. Calc Var Partial Differ Equ, 1994, 2: 29-48 doi: 10.1007/BF01234314
[10]	Cingolani S, Clapp M, Secchi S. Multiple solutions to a magnetic nonlinear Choquard equation. Z Angew Math Phys, 2012, 63: 233-248 doi: 10.1007/s00033-011-0166-8
[11]	Clapp M, Ding Y H. Positive solutions for a Schrödinger equation with critical nonlinearity. Z Angew Math Phys, 2004, 55(4): 592-605 doi: 10.1007/s00033-004-1084-9
[12]	Gao F S, Da Silva E D, Yang M B, Zhou J Z. Existence of solutions for critical Choquard equations via the concentration compactness method. Proc R Soc Edinb Sect A Math, 2020, 150(2): 921-954 doi: 10.1017/prm.2018.131
[13]	Gao F S, Yang M B. On the Brezis-Nirenberg type critical problem for nonlinear Choquard equation. Sci China Math, 2018, 61(7): 1219-1242 doi: 10.1007/s11425-016-9067-5
[14]	Ghimenti M, Pagliardini D. Multiple positive solutions for a slightly subcritical Choquard problem on bounded domains. Calc Var Partial Differ Equ, 2019, 58(5): 1-21 doi: 10.1007/s00526-018-1462-3
[15]	Goel D. The effect of topology on the number of positive solutions of elliptic equation involving Hardy-Littlewood-Sobolev critical exponent. Topol Methods Nonlinear Anal, 2019, 54(2): 751-771
[16]	Goel D, Rădulescu V D, Sreenadh K. Coron problem for nonlocal equations involving Choquard Nonlinearity. Adv Nonlinear Stud, 2020, 20(1): 141-161 doi: 10.1515/ans-2019-2064
[17]	Goel D, Sreenadh K. Critical growth elliptic problems involving Hardy-Littlewood-Sobolev critical exponent in non-contractible domains. Adv Nonlinear Anal, 2020, 9(1): 803-835
[18]	Lieb E H. Existence and uniqueness of the minimizing solution Choquard's nonlinear equations. Stud Appl Math, 1977, 57: 93-105 doi: 10.1002/sapm.v57.2
[19]	Lieb E H, Loss M. Analysis. Rhode Island: AMS, 2001
[20]	Ma P, Zhang J H. Existence and multiplicity of solutions for fractional Choquard. Nonlinear Anal, 2017, 164: 100-117 doi: 10.1016/j.na.2017.07.011
[21]	Lions P L. The Choquard equation and related questions. Nonlinear Anal, 1980, 4(6): 1063-1072 doi: 10.1016/0362-546X(80)90016-4
[22]	Moroz V, Van Schaftingen J. A guide to the Choquard equation. J Fixed Point Theory Appl, 2017, 19(1): 773-813 doi: 10.1007/s11784-016-0373-1
[23]	Moroz V, Van Schaftingen J. Ground states of nonlinear Choquard equations: Existence, qualitative properties and decay asymptotics. J Funct Anal, 2013, 265: 153-184 doi: 10.1016/j.jfa.2013.04.007
[24]	Moroz V, Van Schaftingen J. Existence of groundstates for a class of nonlinear Choquard equations. Trans Am Math Soc, 2015, 367(9): 6557-6579 doi: 10.1090/tran/2015-367-09
[25]	Moroz V, Van Schaftingen J. Semi-classical states for the Choquard equation. Calc Var Partial Differ Equ, 2015, 52(1/2): 199-235 doi: 10.1007/s00526-014-0709-x
[26]	Palatucci G, Pisante A. Improved Sobolev embeddings, profile decomposition and concentration compactness fractional Sobolev space. Calc Var Partial Differ Equ, 2014, 50(3/4): 799-829 doi: 10.1007/s00526-013-0656-y
[27]	Pekar S. Untersuchung über die Elektronentheorie der Kristalle. Berlin: Akademie Berlag, 1954
[28]	Shen Z F, Gao F S, Yang M B. On critical Choquard equation with potential well. Discrete Contin Dyn Syst, 2018, 38(7): 3567-3593 doi: 10.3934/dcds.2018151
[29]	Willem M. Minimax Theorems, Progress in Nonlinear Differential Equations and Their Applications. Boston: Birkhäuser, 1996, 24
[30]	Xu Z Y, Yang J F. Multiple solutions to multi-critical Schrödinger equations. Adv Nonlinear Stud, 2022, 22(1): 273-288 doi: 10.1515/ans-2022-0014
[31]	Yang J F, Zhu L P. Multiple solutions to Choquard equation in exterior domain. J Math Anal Appl, 2022, 507(1): 125726 doi: 10.1016/j.jmaa.2021.125726

Metrics

Viewed

Full text

184

HTML			PDF

Just accepted	Online first	Issue	Just accepted	Online first	Issue
0	0	3	0	0	181

	From	local

	Times	184
	Rate	100%

Abstract

Just accepted	Online first	Issue

0	0	92

	From	Others

	Times	92
	Rate	100%

Cited

Web of Science	Crossref	ScienceDirect	Search for Citations in Google Scholar >>


This page requires you have already subscribed to WoS.

Shared

Discussed