数学物理学报 ›› 2023, Vol. 43 ›› Issue (4): 1197-1120.
大振幅浅水波模型的柯西问题研究
- 重庆师范大学数学科学学院 重庆市 401331
-
收稿日期:2022-07-08修回日期:2023-02-11出版日期:2023-08-26发布日期:2023-07-03 -
通讯作者:周寿明 E-mail:137306468@qq.com;zhoushouming76@163.com -
作者简介:蔡森林, E-mail:137306468@qq.com -
基金资助:国家自然科学基金(11971082);重庆市自然科学基金项目(csts2020jcyj-jqX0022);重庆英才青年拔尖人才(cstc2021ycjh-bgzxm0130);重庆市教育委员会科学技术研究项目(KJZD-M202200501);重庆市教育委员会科学技术研究项目(KJZD-M201900501);重庆市教育委员会科学技术研究项目(KJQN202000518);重庆市留学人员回国创业创新支持计划(cx2022029)
On the Cauchy Problem for a Shallow Water Regime of Waves with Large Amplitude
Cai Senlin( ),Zhou Shouming*(
),Zhou Shouming*( ),Chen Rong
),Chen Rong
- College of Mathematics Science, Chongqing Normal University, Chongqing 401331
-
Received:2022-07-08Revised:2023-02-11Online:2023-08-26Published:2023-07-03 -
Contact:Shouming Zhou E-mail:137306468@qq.com;zhoushouming76@163.com -
Supported by:National Natural Science Foundation of China(11971082);Natural Science Foundation of Chongqing(csts2020jcyj-jqX0022);Chongqing's Youth Talent Support Program(cstc2021ycjh-bgzxm0130);Science and Technology Research Program of Chongqing Municipal Educational Commission(KJZD-M202200501);Science and Technology Research Program of Chongqing Municipal Educational Commission(KJZD-M201900501);Science and Technology Research Program of Chongqing Municipal Educational Commission(KJQN202000518);Entrepreneurship and Innovation Support Plan of Chongqing for Returned Overseas Scholars(cx2022029)
摘要:
该文考虑单参数族浅水波方程的柯西问题, 该模型是在参数








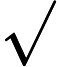

















 <
<



















中图分类号:
- O175.29
引用本文
蔡森林,周寿明,陈容. 大振幅浅水波模型的柯西问题研究[J]. 数学物理学报, 2023, 43(4): 1197-1120.
Cai Senlin,Zhou Shouming,Chen Rong. On the Cauchy Problem for a Shallow Water Regime of Waves with Large Amplitude[J]. Acta mathematica scientia,Series A, 2023, 43(4): 1197-1120.
使用本文
| [1] |
Aldroubi A, Gröchenig K. Nonuniform sampling and reconstruction in shift-invariant spaces. SIAM Rev, 2001, 43: 585-620
doi: 10.1137/S0036144501386986 |
| [2] |
Basu B, Haziot S V, Staino A. Wave breaking for periodic solutions of a nonlinear shallow water equation. Applicable Analysis, 2022, 101(2): 519-526
doi: 10.1080/00036811.2020.1750603 |
| [3] | Benjamin T B, Bona J L, Mahony J J. Model equations for long waves in nonlinear dispersive systems. Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 1972, 272(1220): 47-78 |
| [4] | Brandolese L. Breakdown for the Camassa-Holm equation using decay criteria and persistence in weighted spaces. International Mathematics Research Notices, 2012, 22: 5161-5181 |
| [5] |
Camassa R, Holm D D. An integrable shallow water equation with peaked solitons. Physical Review Letters, 1993, 71(11): 1661-1664
doi: 10.1103/PhysRevLett.71.1661 pmid: 10054466 |
| [6] |
Constantin A. Existence of permanent and breaking waves for a shallow water equation: a geometric approach. Annales de l'institut Fourier, 2000, 50(2): 321-362
doi: 10.5802/aif.1757 |
| [7] | Constantin A, Escher J. Global existence and blow-up for a shallow water equation. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze, 1998, 26(2): 303-328 |
| [8] | Constantin A, Escher J. Analyticity of periodic traveling free surface water waves with vorticity. Annals of Mathematics, 2011: 559-568 |
| [9] |
Constantin A, Lannes D. The hydrodynamical relevance of the Camassa-Holm and Degasperis-Procesi equations. Archive for Rational Mechanics and Analysis, 2009, 192(1): 165-186
doi: 10.1007/s00205-008-0128-2 |
| [10] |
Constantin A, Strauss W A. Stability of peakons. Communications on Pure and Applied Mathematics. 2000, 53(5): 603-610
doi: 10.1002/(ISSN)1097-0312 |
| [11] |
Constantin A, Strauss W A. Stability of the Camassa-Holm Solitons. Journal of Nonlinear Science, 2002, 12(4): 415-422
doi: 10.1007/s00332-002-0517-x |
| [12] |
Fan L, Yan W. On the weak solutions and persistence properties for the variable depth KDV general equations. Nonlinear Analysis: Real World Applications, 2018, 44: 223-245
doi: 10.1016/j.nonrwa.2018.05.002 |
| [13] | Escher J, Yin Z. Well-posedness, blow-up phenomena, and global solutions for the b-equation. 2008, 624: 51-80 |
| [14] |
Fan L, Yan W. The Cauchy problem for shallow water waves of large amplitude in Besov space. Journal of Differential Equations, 2019, 267(3): 1705-1730
doi: 10.1016/j.jde.2019.02.019 |
| [15] | Gasull A, Geyer A. Traveling surface waves of moderate amplitude in shallow water. Nonlinear Analysis: Theory, Methods & Applications, 2014, 102: 105-119 |
| [16] | Geyer A. Solitary traveling water waves of moderate amplitude. Journal of Nonlinear Mathematical Physics, 2012, 19(supp01): 1240010 |
| [17] |
Geyer A, Quirchmayr R. Traveling wave solutions of a highly nonlinear shallow water equation. Discrete and Continuous Dynamical Systems, 2018, 38(3): 1567-1604
doi: 10.3934/dcds.2018065 |
| [18] |
Guo Y, Wu Y, Lai S, et al. The global weak solution for the shallow water wave model of moderate amplitude. Applicable Analysis, 2017, 96(4): 663-678
doi: 10.1080/00036811.2016.1151496 |
| [19] |
Himonas A A, Holliman C. On well-posedness of the Degasperis-Procesi equation. Discrete and Continuous Dynamical Systems, 2011, 31(2): 469-488
doi: 10.3934/dcds.2011.31.469 |
| [20] | Himonas A A, Holliman C. The Cauchy problem for a generalized Camassa-Holm equation. Adv Differential Equations, 2014, 19: 161-200 |
| [21] | Himonas A A, Kenig C. Non-uniform dependence on initial data for the CH equation on the line. Differential Integral Equations, 2009, 22: 201-224 |
| [22] |
Himonas A A, Kenig C, Misiolek G. Non-uniform dependence for the periodic CH equation. Communications in Partial Differential Equations, 2010, 35(6): 1145-1162
doi: 10.1080/03605300903436746 |
| [23] |
Himonas A A, Mantzavinos D. Hölder continuity for the Fokas-Olver-Rosenau-Qiao equation. Journal of Nonlinear Science, 2014, 24: 1105-1124
doi: 10.1007/s00332-014-9212-y |
| [24] |
Jiang B, Zhou Y. Cusped solitary wave with algebraic decay governed by the equation for surface waves of moderate amplitude. Journal of Nonlinear Mathematical Physics, 2020, 27(2): 219-226
doi: 10.1080/14029251.2020.1700632 |
| [25] | Kato T. Quasi-linear Equations of Evolution, with Applications to Partial Differential Equations//Everitt W N. Spectral Theory and Differential Equations. Berlin: Springer, 2006: 25-70 |
| [26] |
Korteweg D J, De Vries G X. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1895, 39(240): 422-443
doi: 10.1080/14786449508620739 |
| [27] | Li J, Kou K I. Dynamics of traveling wave solutions to a new highly nonlinear shallow water wave equation. International Journal of Bifurcation and Chaos, 2017, 27(03): 1750044 |
| [28] | Liu X, Liu J. On the low regularity solutions and wave breaking for an equation modeling shallow water waves of moderate amplitude. Nonlinear Analysis: Theory, Methods & Applications, 2014, 107}: 1-11 |
| [29] |
Mi Y, Mu C. On the solutions of a model equation for shallow water waves of moderate amplitude. Journal of Differential Equations, 2013, 255(8): 2101-2129
doi: 10.1016/j.jde.2013.06.008 |
| [30] |
Mutlubaş N D. On the Cauchy problem for a model equation for shallow water waves of moderate amplitude. Nonlinear Analysis: Real World Applications, 2013, 14(5): 2022-2026
doi: 10.1016/j.nonrwa.2013.02.006 |
| [31] | Mutlubaş N D. Local well-posedness and wave breaking results for periodic solutions of a shallow water equation for waves of moderate amplitude. Nonlinear Analysis: Theory, Methods & Applications, 2014, 97: 145-154 |
| [32] |
Mutlubaş N D, Geyer A. Orbital stability of solitary waves of moderate amplitude in shallow water. Journal of Differential Equations, 2013, 255(2): 254-263
doi: 10.1016/j.jde.2013.04.010 |
| [33] | Mutlubaş N D, Geyer A, Matioc B V. Non-uniform continuity of the flow map for an evolution equation modeling shallow water waves of moderate amplitude. Nonlinear Analysis: Real World Applications, 2014, 17}: 322-331 |
| [34] | Mutlubaş N D, Geyer A, Quirchmayr R. Well-posedness of a highly nonlinear shallow water equation on the circle. Nonlinear Analysis, 2020, 197: 11184917: 322-331 |
| [35] |
Quirchmayr R. A new highly nonlinear shallow water wave equation. Journal of Evolution Equations, 2016, 16: 539-567
doi: 10.1007/s00028-015-0312-4 |
| [36] | Wang Y. The existence of global weak solutions to the shallow water wave model with moderate amplitude. Cogent Mathematics, 2016, 3(1): 1155829 |
| [37] |
Yang X, Wu X. Wave breaking and presistent decay of solution to a shallow water wave equation. Discrete Continuous Dynamical Systems-Series S, 2016, 9(6): 2149-2165
doi: 10.3934/dcdss |
| [38] |
Yang S, Xu T. Well-posedness and persistence property for a shallow water wave equation for waves of large amplitude. Applicable Analysis, 2019, 98(5): 981-990
doi: 10.1080/00036811.2017.1408079 |
| [39] | Yin Z. On the Cauchy problem for an integrable equation with peakon solutions. Illinois Journal of Mathematics, 2003, 47(3): 649-666 |
| [40] |
Zhou S. The local well-posedness, existence and uniqueness of weak solutions for a model equation for shallow water waves of moderate amplitude. Journal of Differential Equations, 2015, 258(12): 4103-4126
doi: 10.1016/j.jde.2015.01.014 |
| [41] |
Zhou S. Well-posedness and wave breaking for a shallow water wave model with large amplitude. Journal of Evolution Equations, 2020, 20(1): 141-163
doi: 10.1007/s00028-019-00518-4 |
| [42] |
Zhou S, Mu C. Global conservative solutions for a model equation for shallow water waves of moderate amplitude. Journal of Differential Equations, 2014, 256(5): 1793-1816
doi: 10.1016/j.jde.2013.11.011 |
| [43] |
Zhou S, Qiao Z, Mu C, et al. Continuity and asymptotic behaviors for a shallow water wave model with moderate amplitude. Journal of Differential Equations, 2017, 263(2): 910-933
doi: 10.1016/j.jde.2017.03.002 |
| [44] | Zhou S, Wang B, Chen R. Non-uniform dependence on initial data for the periodic Constantin-Lannes equation. Journal of Mathematical Physics, 2018, 59(3): 031502 |
| [1] | 建芒芒, 郑素佩, 封建湖, 翟梦情. 浅水波方程熵稳定格式的保平衡性[J]. 数学物理学报, 2023, 43(2): 491-504. |
| [2] | 欧阳柏平. 非线性记忆项的Euler-Poisson-Darboux-Tricomi方程解的爆破[J]. 数学物理学报, 2023, 43(1): 169-180. |
| [3] | 冯美强, 张学梅. Monge-Ampère方程边界爆破解的最优估计和不存在性[J]. 数学物理学报, 2023, 43(1): 181-202. |
| [4] | 胡振祥,聂麟飞. 具有水平传播和环境传播的反应扩散传染病模型研究[J]. 数学物理学报, 2022, 42(6): 1849-1860. |
| [5] | 鲁呵倩,张正策. 带非线性梯度项的p-Laplacian抛物方程的临界指标[J]. 数学物理学报, 2022, 42(5): 1381-1397. |
| [6] | 万雅琪,陈晓莉. 压力项属于Triebel-Lizorkin空间的三维不可压Navier-Stokes方程的正则性准则[J]. 数学物理学报, 2022, 42(5): 1473-1481. |
| [7] | 邱臻,王光武. 量子Navier-Stokes-Landau-Lifshitz方程光滑解的爆破问题[J]. 数学物理学报, 2022, 42(4): 1074-1088. |
| [8] | 何春蕾,刘子慧. 一类双曲平均曲率流的对称与整体解[J]. 数学物理学报, 2022, 42(4): 1089-1102. |
| [9] | 杨连峰,曾小雨. 拟相对论薛定谔方程基态解的存在性与爆破行为[J]. 数学物理学报, 2022, 42(1): 165-175. |
| [10] | 孙丹丹,李盈科,滕志东,张太雷. 具有年龄结构的麻疹传染病模型的稳定性分析[J]. 数学物理学报, 2021, 41(6): 1950-1968. |
| [11] | 杜玉阁,田书英. 一类带对数非线性项的抛物方程解的存在性和爆破[J]. 数学物理学报, 2021, 41(6): 1816-1829. |
| [12] | 合敬然,郭合林,王文清. 一类带强制位势的p-Laplace特征值问题[J]. 数学物理学报, 2021, 41(5): 1323-1332. |
| [13] | 杨慧,韩玉柱. 一类抛物型Kirchhoff方程解的爆破性质[J]. 数学物理学报, 2021, 41(5): 1333-1346. |
| [14] | 欧阳柏平,肖胜中. 具有非线性记忆项的半线性双波动方程解的全局非存在性[J]. 数学物理学报, 2021, 41(5): 1372-1381. |
| [15] | 陈明涛,苏文火,臧爱彬. 带真空无磁扩散不可压磁流体方程柯西问题的局部适定性[J]. 数学物理学报, 2021, 41(1): 100-125. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 112
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 90
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|