数学物理学报 ›› 2022, Vol. 42 ›› Issue (2): 502-519.
一类描述肿瘤入侵与具有信号依赖机制的趋化模型有界性与稳定性分析
- 1 深圳技术大学大数据与互联网学院 广东 深圳 518118
2 华南理工大学数学学院 广州 510640
-
收稿日期:2020-12-03出版日期:2022-04-26发布日期:2022-04-18 -
通讯作者:赵晖 E-mail:shishijie@sztu.edu.cn -
基金资助:国家自然科学基金(62172164);国家自然科学基金(12026608);国家自然科学基金(11971176);国家自然科学基金(11901400)
Boundedness and Stabilization of a Chemotaxis Model Describing Tumor Invasion with Signal-Dependent Motility
Shijie Shi1,Zhengrong Liu2,Hui Zhao2,*( )
)
- 1 College of Big Data and Internet, Shenzhen Technology University, Guangdong Shenzhen 518118
2 School of Mathematics, South China University of Technology, Guangzhou 510640
-
Received:2020-12-03Online:2022-04-26Published:2022-04-18 -
Contact:Hui Zhao E-mail:shishijie@sztu.edu.cn -
Supported by:the NSFC(62172164);the NSFC(12026608);the NSFC(11971176);the NSFC(11901400)
摘要:
该文将研究如下问题 

























































































































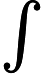













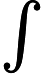













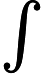





中图分类号:
- O175.2
引用本文
史诗洁,刘正荣,赵晖. 一类描述肿瘤入侵与具有信号依赖机制的趋化模型有界性与稳定性分析[J]. 数学物理学报, 2022, 42(2): 502-519.
Shijie Shi,Zhengrong Liu,Hui Zhao. Boundedness and Stabilization of a Chemotaxis Model Describing Tumor Invasion with Signal-Dependent Motility[J]. Acta mathematica scientia,Series A, 2022, 42(2): 502-519.
使用本文
| 1 |
Ahn J , Yoon C . Global well-posedness and stability of constant equilibria in parabolicelliptic chemotaxis systems without gradinet sensing. Nonlinearity, 2019, 32 (4): 1327- 1351
doi: 10.1088/1361-6544/aaf513 |
| 2 | Amann H . Dynamic theory of quasilinear parabolic equations. Ⅱ: Reaction-diffusion systems. Differ Integral Equ, 1990, 3: 13- 75 |
| 3 | Amann H. Nonhomogeneous linear and quasilinear elliptic and parabolic boundary value problems// Schmeisser H, Triebel H. Function Spaces, Differential Operators and Nonlinear Analysis. Wiesbaden: Vieweg+Teubner Verlag, 1993, 133: 9-126 |
| 4 |
Bellomo N , Bellouquid A , Tao Y S , Winkler M . Towards a mathematical theory of Keller-Segel models of pattern formation in biological tissues. Math Models Methods Appl Sci, 2015, 25: 1663- 1763
doi: 10.1142/S021820251550044X |
| 5 | Chaplain M, Anderson A. Mathematical modelling of tissue invasion//Preziosi L. Cancer Modelling and Simulation. Boca Raton, FL: Chapman Hall/CRC, 2003: 269-297 |
| 6 |
Cie'slak T , Stinner C . Finite-time blowup and global-in-time unbounded solutions to a parabolic-parabolic quasilinear Keller-Segel system in higher dimensions. J Diff Equ, 2012, 252: 5832- 5851
doi: 10.1016/j.jde.2012.01.045 |
| 7 |
Cie'slak T , Stinner C . New critical exponents in a fully parabolic quasilinear Keller-Segel system and applications to volume filling models. J Diff Equ, 2015, 258: 2080- 2113
doi: 10.1016/j.jde.2014.12.004 |
| 8 |
Cie'slak T , Winkler M . Finite-time blow-up in a quasilinear system of chemotaxis. Nonlinearity, 2008, 21: 1057- 1076
doi: 10.1088/0951-7715/21/5/009 |
| 9 |
Cie'slak T , Winkler M . Stabilization in a higher-dimensional quasilinear Keller-Segel system with exponentially decaying diffusivity and subcritical sensitivity. Nolinear Anal, 2017, 159: 129- 144
doi: 10.1016/j.na.2016.04.013 |
| 10 |
Cie'slak T , Winkler M . Global bounded solutions in a two-dimensional quasilinear Keller-Segel system with exponentially decaying diffusivity and subcritical sensitivity. Nonlinear Anal Real World Appl, 2017, 35: 1- 19
doi: 10.1016/j.nonrwa.2016.10.002 |
| 11 |
Fu X , Tang L , Liu C , et al. Stripe formation in bacterial system with density-suppressed motility. Phys Rev Lett, 2012, 108: 198102
doi: 10.1103/PhysRevLett.108.198102 |
| 12 | Fujie K , Ito A , Yokota T . Existence and uniqueness of local classical solutions to modified tumor invasion models of Chaplain-Anderson type. Adv Math Sci Appl, 2014, 24: 67- 84 |
| 13 | Fujie K , Ito A , Winkler M , Yokota T . Stabilization in a chemotaxis model for tumor invasion. Discrete Contin Dyn Syst, 2016, 36: 151- 169 |
| 14 | Herrero M A , Vel'azquez J L . A blow-up mechanism for a chemotaxis model. Ann Scuola Norm Sup Pisa Cl Sci, 1997, 24: 633- 683 |
| 15 |
Hillen T , Potapov A . The one-dimensional chemotaxis model: global existence and asymptotic profile. Math Methods Appl Sci, 2004, 27: 1783- 1801
doi: 10.1002/mma.569 |
| 16 |
Horstmann D , Winkler M . Boundedness vs blow-up in a chemotaxis system. J Diff Equ, 2005, 215: 52- 107
doi: 10.1016/j.jde.2004.10.022 |
| 17 |
Hu B , Tao Y S . To the exclusion of blow-up in a three-dimensional chemotaxis-growth model with indirect attractant production. Math Models Methods Appl Sci, 2016, 26: 2111- 2128
doi: 10.1142/S0218202516400091 |
| 18 |
Ishida S , Seki K , Yokota T . Boundedness in quasilinear Keller-Segel systems of parabolic-parabolic type on non-convex bounded domains. J Diff Equ, 2014, 256: 2993- 3010
doi: 10.1016/j.jde.2014.01.028 |
| 19 |
J  doi: 10.1090/S0002-9947-1992-1046835-6 |
| 20 |
Jin H Y , Kim Y J , Wang Z A . Boundedness, stabilization, and pattern formation driven by density-suppressed motility. SIAM J Appl Math, 2018, 78: 1632- 1657
doi: 10.1137/17M1144647 |
| 21 |
Jin H Y , Liu Z , Shi S . Global dynamics of a quasilinear chemotaxis model arising from tumor invasion. Nonlinear Anal Real World Appl, 2018, 44: 18- 39
doi: 10.1016/j.nonrwa.2018.04.006 |
| 22 |
Jin H Y , Liu Z , Shi S , Xu J . Boundedness and stabilization in two-species chemotaxiscompetition system with signal-dependent diffusion and sensitivity. J Diff Equ, 2019, 267: 494- 524
doi: 10.1016/j.jde.2019.01.019 |
| 23 | Jin H Y , Wang Z A . Global dynamics and spatio-temporal patterns of predator-prey systems with density-dependent motion. European J of Appl Math, 2020, 32 (4): 1- 31 |
| 24 |
Jin H Y , Xiang T . Boundedness and exponential convergence in a chemotaxis model for tumor invasion. Nonlinearity, 2016, 29: 3579- 3596
doi: 10.1088/0951-7715/29/12/3579 |
| 25 | Ladyzhenskaya O A, Solonnikov V A, Uralceva N N. Linear and Quasilinear Equations of Parabolic Type. Providence, RI: Amer Math Soc, 1968 |
| 26 |
Liu C . Sequential establishment of stripe patterns in an expanding cell population. Sci, 2011, 334: 238- 241
doi: 10.1126/science.1209042 |
| 27 |
Lou Y , Winkler M . Global existence and uniform boundedness of smooth solutions to a cross-diffusion system with equal diffusion rates. Comm Part Diff Equ, 2015, 40 (10): 1905- 1941
doi: 10.1080/03605302.2015.1052882 |
| 28 |
Mizoguchi N , Souplet P . Nondegeneracy of blow-up points for the parabolic Keller-Segel system. Ann Inst H Poincar'e Anal Non Lin'eaire, 2014, 31: 851- 875
doi: 10.1016/j.anihpc.2013.07.007 |
| 29 | Nagai T . Blow-up of radially symmetric solutions to a chemotaxis system. Adv Math Sci Appl, 1995, 5: 581- 601 |
| 30 | Senba T , Yoshida K . Application of the Trudinger-Moser inequality to a parabolic system of chemotaxis. Funkcial Ekvac, 1997, 40: 411- 433 |
| 31 | Osaki K , Yagi A . Finite dimensional attractor for one-dimensional Keller-Segel equations. Funkcial Ekvac, 2001, 44: 441- 469 |
| 32 |
Porzio M , Vespri V . H  doi: 10.1006/jdeq.1993.1045 |
| 33 |
Senba T , Suzuki T . Parabolic system of chemotaxis: blowup in a finite and the infinite time. Methods Appl Anal, 2001, 8: 349- 367
doi: 10.4310/MAA.2001.v8.n2.a9 |
| 34 | Souplet P, Quittner P. Superlinear Parabolic Problems: Blow-up, Global Existence and Steady States. Boston: Birkauser, 2007 |
| 35 |
Stinner C , Surulescu C , Winkler M . Global weak solutions in a PDE-ODE system modeling multiscale cancer cell invasion. SIAM J Math Anal, 2014, 46: 1969- 2007
doi: 10.1137/13094058X |
| 36 |
Tao Y S , Winkler M . Boundedness in a quasilinear parabolic-parabolic Keller-Segel system with subcritical sensitivity. J Diff Equ, 2012, 252: 692- 715
doi: 10.1016/j.jde.2011.08.019 |
| 37 |
Tao Y S , Winkler M . Large time behavior in a multidimensional chemotaxis haptotaxis model with slow signal diffusion. SIAM J Math Anal, 2015, 47: 4229- 4250
doi: 10.1137/15M1014115 |
| 38 |
Tao Y S , Winkler M . Critical mass for infinite-time aggregation in a chemotaxis model with indirect signal production. J Eur Math Soc(JEMS), 2017, 19: 3641- 3678
doi: 10.4171/JEMS/749 |
| 39 | Tao Y S , Winkler M . Effects of signal-dependent motilities in a Keller-Segel-type reaction-diffusion system. Math Models Meth Appl Sci, 2017, 27 (19): 1645- 1683 |
| 40 |
Wang Z A , Hillen T . Classical solutions and pattern formation for a volume filling chemotaxis model. Chaos, 2007, 17: 037108
doi: 10.1063/1.2766864 |
| 41 |
Winkler M . Aggregation vs global diffusive behavior in the higher-dimensional Keller-Segel model. J Diff Equ, 2010, 248: 2889- 2905
doi: 10.1016/j.jde.2010.02.008 |
| 42 |
Winkler M . Does a "volume-filling effect" always prevent chemotactic collapse?. Math Methods Appl Sci, 2010, 33: 12- 24
doi: 10.1002/mma.1146 |
| 43 |
Winkler M . Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller-Segel system. J Math Pures Appl, 2013, 100: 748- 767
doi: 10.1016/j.matpur.2013.01.020 |
| 44 |
Winkler M . Aggregation vs global diffusive behavior in the higher-dimensional Keller-Segel model. J Diff Equ, 2010, 248: 2889- 2905
doi: 10.1016/j.jde.2010.02.008 |
| [1] | 张再云,刘振海,邓又军. 具有时变时滞和速度相关材料密度的非线性粘弹性方程的整体存在性和一般衰减性[J]. 数学物理学报, 2021, 41(6): 1684-1704. |
| [2] | 贾哲,杨作东. 带非线性扩散项和信号产生项的趋化-趋触模型解的整体有界性[J]. 数学物理学报, 2021, 41(5): 1382-1395. |
| [3] | 王娟,原子霞. 具有对数敏感度和混合边界的一维趋化模型解的整体存在性和收敛性[J]. 数学物理学报, 2020, 40(6): 1646-1669. |
| [4] | 邱华, 张颖姝, 房少梅. 不可压粘弹性流体的Leray-α-Oldroyd模型整体解的存在性[J]. 数学物理学报, 2017, 37(1): 102-112. |
| [5] | 张宏伟, 刘功伟, 呼青英. 一类具对数源项波动方程的初边值问题[J]. 数学物理学报, 2016, 36(6): 1124-1136. |
| [6] | 刘洋. 位势井及其对具临界初始能量的非牛顿渗流方程的应用[J]. 数学物理学报, 2016, 36(6): 1211-1220. |
| [7] | 狄华斐, 尚亚东. 一类带有非线性阻尼项和源项的四阶波动方程整体解的存在性与不存在性[J]. 数学物理学报, 2015, 35(3): 618-633. |
| [8] | 沈继红, 张明有, 杨延冰, 刘博为, 徐润章. 具阻尼的高维广义Boussinesq 方程的Cauchy 问题的整体适定性[J]. 数学物理学报, 2014, 34(5): 1173-1187. |
| [9] | 米永生, 穆春来, 吴云龙. 具有多重非线性的非牛顿多方渗流方程的整体存在性与非存在性[J]. 数学物理学报, 2014, 34(3): 626-637. |
| [10] | 凌征球, 周泽文. 非局部边界条件的退化抛物方程组解的爆破和整体存在性[J]. 数学物理学报, 2014, 34(2): 338-346. |
| [11] | 曲风龙, 王玉泉. 一类带有趋化性扩散的细菌模型一致有界解的整体存在性[J]. 数学物理学报, 2014, 34(2): 409-418. |
| [12] | 毛剑峰, 黎野平. 三维双极Euler-Poisson方程初值问题光滑解的整体存在性和渐近性[J]. 数学物理学报, 2013, 33(3): 510-522. |
| [13] | 王术, 冯跃红, 李新. 双极可压缩等熵Euler-Maxwell系统光滑周期解的整体存在性[J]. 数学物理学报, 2012, 32(6): 1041-1049. |
| [14] | 凌征球, 卢伟明, 周泽文. 带非局部边界条件的半线性抛物系统的一致爆破模式[J]. 数学物理学报, 2012, 32(2): 433-440. |
| [15] | 杨志坚, 程建玲. Kirchhoff型方程解的渐近行为[J]. 数学物理学报, 2011, 31(4): 1008-1021. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 128
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 99
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||||||
|