临界Schrödinger映射非齐次初边值问题的有限差分格式

数学物理学报 ›› 2021, Vol. 41 ›› Issue (5): 1311-1322.

临界Schrödinger映射非齐次初边值问题的有限差分格式

邓海云¹(),刘辉^2,*(),宋文静³()

¹ 南京审计大学应用数学系南京 211815
² 曲阜师范大学数学科学学院山东曲阜 273165
³ 西安工程大学理学院西安 710048

收稿日期:2020-08-13 出版日期:2021-10-26 发布日期:2021-10-08
通讯作者: 刘辉 E-mail:haiyundengmath1989@njust.edu.cn;liuhuinanshi@qfnu.edu.cn;wenjingsong1@163.com
作者简介:邓海云, E-mail: haiyundengmath1989@njust.edu.cn|宋文静, E-mail: wenjingsong1@163.com
基金资助:
国家自然科学基金(12001276);国家自然科学基金(12001275);国家自然科学基金(12071219);国家自然科学基金(11901342);国家自然科学基金(12001415);山东省自然科学基金(ZR2018QA002);中国博士后科学基金(2019M652350)

Finite Difference Scheme for the Nonhomogeneous Initial Boundary Value Problem of Critical Schrödinger Map

Haiyun Deng¹(),Hui Liu^2,*(),Wenjing Song³()

¹ Department of Applied Mathematics, Nanjing Audit University, Nanjing 211815
² School of Mathematical Sciences, Qufu Normal University, Shandong Qufu 273165
³ College of Science, Xi'an Polytechnic University, Xi'an 710048

Received:2020-08-13 Online:2021-10-26 Published:2021-10-08
Contact: Hui Liu E-mail:haiyundengmath1989@njust.edu.cn;liuhuinanshi@qfnu.edu.cn;wenjingsong1@163.com
Supported by:
the NSFC(12001276);the NSFC(12001275);the NSFC(12071219);the NSFC(11901342);the NSFC(12001415);the NSF of Shandong Province(ZR2018QA002);the China Postdoctoral Science Foundation(2019M652350)

摘要/Abstract

摘要：

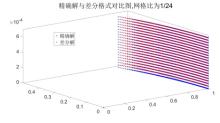
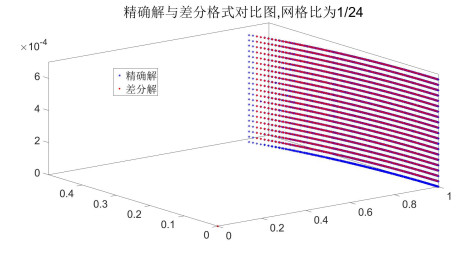
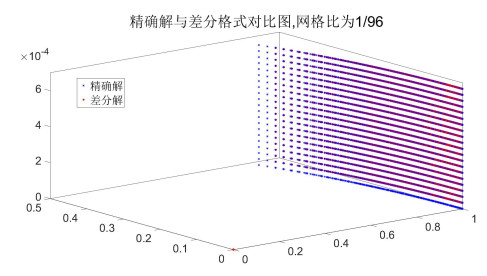
利用有限差分格式考虑了具有非齐次初边值条件的临界Schrödinger映射的数值解，证明了其收敛性及稳定性，并通过数值实验表明，格式具有较好的有效性和稳定性.

关键词: Schrödinger映射, 差分格式, 收敛性, 稳定性

Abstract:

In this paper, we study finite difference scheme for the nonhomgeneous initial boundary value problem of critical Schrödinger map in two-dimensional space. We get the convergence and stability of the difference scheme. At the same time, we prove that this difference scheme has good effectiveness and stability by numerical experiments.

Key words: Schrödinger map, Difference scheme, Convergence, Stability

中图分类号:

O241.82

邓海云,刘辉,宋文静. 临界Schrödinger映射非齐次初边值问题的有限差分格式[J]. 数学物理学报, 2021, 41(5): 1311-1322.

Haiyun Deng,Hui Liu,Wenjing Song. Finite Difference Scheme for the Nonhomogeneous Initial Boundary Value Problem of Critical Schrödinger Map[J]. Acta mathematica scientia,Series A, 2021, 41(5): 1311-1322.

图/表 3

图 1

图 2

表 1

参考文献 28

1	Angenent S B , Hulshof J , Matano H . The radius of vanishing bubbles in equivariant harmonic map flow from D² to S². SIAM J Math Anal, 2009, 41 (3): 1121- 1137 doi: 10.1137/070706732
2	Bejenaru I , Ionescu A D , Kenig C E , Tataru D . Global Schrödinger maps in dimensions d ≥ 2:small data in the critical Sobolev spaces. Ann of Math, 2011, 173 (2): 1443- 1506
3	Cimrák I . Convergence result for the constraint preserving mid-point scheme for micromagnetism. J Comput Appl Math, 2009, 228 (1): 238- 246 doi: 10.1016/j.cam.2008.09.017
4	Dodson B , Smith P . A controlling norm for energy-critical Schrödinger maps. Trans Amer Math Soc, 2015, 367 (10): 7193- 7220 doi: 10.1090/S0002-9947-2015-06417-4
5	E W N , Wang X P . Numerical methods for the Landau-Lifshitz equation. SIAM J Numer Anal, 2000, 38 (5): 1647- 1665 doi: 10.1137/S0036142999352199
6	Gilbarg D , Trudinger N S . Elliptic Partial Differential Equations of Second Order. New York: Springer-Verlag, 1983
7	Guo B L , Han Y Q . Global smooth solution of hydrodynamical equation for the Heisenberg paramagnet. Math Methods Appl Sci, 2004, 27 (2): 181- 191 doi: 10.1002/mma.450
8	Gustafson S , Kang K , Tsai T P . Schrödinger flow near harmonic maps. Comm Pure Appl Math, 2007, 60 (4): 463- 499 doi: 10.1002/cpa.20143
9	Gustafson S , Kang K , Tsai T P . Asymptotic stability of harmonic maps under the Schrödinger flow. Duke Math J, 2008, 145 (3): 537- 583
10	Gustafson S , Kang K , Tsai T P . Asymptotic stability, concentration, and oscillation in harmonic map heat-flow, Landau-Lifshitz, and Schrödinger maps on $\mathbb{R}.2$. Comm Math Phys, 2010, 300 (1): 205- 242 doi: 10.1007/s00220-010-1116-6
11	Jendrej J . Construction of two-bubble solutions for the energy-critical NLS. Anal PDE, 2017, 10 (8): 1923- 1959 doi: 10.2140/apde.2017.10.1923
12	Kim E , Lipnikov K . The mimetic finite difference method for the Landau-Lifshitz equation. J Comput Phys, 2017, 328, 109- 130 doi: 10.1016/j.jcp.2016.10.016
13	Kim E. Numerical Methods for the Landau-Lifshitz Equation in Micromagnetics: The Mimetic Finite Difference Method and the Mass-Lumped Finite Element Method[D]. Berkeley: University of California, 2017
14	Krieger J , Miao S . On the stability of blowup solutions for the critical corotational wave-map problem. Duke Math J, 2020, 169 (3): 435- 532
15	Li Z , Zhao L F . Convergence to harmonic maps for the Landau-Lifshitz flows between two dimensional hyperbolic spaces. Discrete Contin Dyn Syst, 2019, 39 (1): 607- 638 doi: 10.3934/dcds.2019025
16	Li P C , Xie C J , Du R , et al. Two improved Gauss-Seidel projection methods for Landau-Lifshitz-Gilbert equation. J Comput Phys, 2020, 401, 109046 doi: 10.1016/j.jcp.2019.109046
17	陆金甫, 关治. 偏微分方程数值解法. 北京: 清华大学出版社, 2004
	Lu J F , Guan Z . Numerical Solution of Partial Differential Equations. Beijing: Tsinghua University Press, 2004
18	吕永强. Landau-Lifshitz方程的有限差分格式与整体正则解[D]. 北京: 中国工程物理研究院, 2004
	Lv Y Q. Finite Difference Format and the Overall Regular Solutions of Landau-Lifshitz Equations[D]. Beijing: Chinese Research Institute of Engineering Physics, 2004
19	Merle F , Raphaël P , Rodnianski I . Blowup dynamics for smooth data equivariant solutions to the critical Schrödinger map problem. Invent Math, 2013, 193 (2): 249- 365 doi: 10.1007/s00222-012-0427-y
20	Mu C L , Liu L M , Wu Y H , Yan L . Some new results for the multidimensional Landau-Lifshitz equations. Phys Lett A, 2008, 372 (43): 6469- 6474 doi: 10.1016/j.physleta.2008.09.006
21	Perelman G . Blow up dynamics for equivariant critical Schrödinger maps. Comm Math Phys, 2014, 330 (1): 69- 105 doi: 10.1007/s00220-014-1916-1
22	Sanchez D . Numerical study of long waves in ferromagnetic media. Numer Methods Partial Differential Equations, 2006, 22 (5): 1127- 1148 doi: 10.1002/num.20142
23	van den Berg J B , Hulshof J , King J R . Formal asymptotics of bubbling in the harmonic map heat flow. SIAM J Appl Math, 2003, 63 (5): 1682- 1717 doi: 10.1137/S0036139902408874
24	杨干山, 刘宪高. Landau-Lifshitz方程派生的球面锥对称族及其演化. 中国科学: 数学, 2011, 41 (2): 181- 196
	Yang G S , Liu X G . Spherical cone symmetric families generated by Landau-Lifshitz equation and their evolution. Sci Sin Math, 2011, 41 (2): 181- 196
25	Yang G S . The difference between Schrödinger equation derived from Schrödinger map and Landau-Lifshitz equation. Phys Lett A, 2012, 376 (4): 231- 235 doi: 10.1016/j.physleta.2011.11.003
26	杨干山, 吴继晖, 郭柏灵. 具有二阶逼近效应场多维Landau-Lifshitz方程解的极限行为. 中国科学: 数学, 2013, 43, 445- 476
	Yang G S , Wu J H , Guo B L . Limiting behavior of solutions to multidimensional Landau-Lifshitz equations with second approximation of effective field. Sci Sin Math, 2013, 43, 445- 476
27	Yang W , Wang D L , Yang L . A stable numerical method for space fractional Landau-Lifshitz equations. Appl Math Lett, 2016, 61, 149- 155 doi: 10.1016/j.aml.2016.05.014
28	Zhou Y L , Guo B L , Tan S B . Existence and uniqueness of smooth solution for system of ferro-magnetic chain. Sci China Ser A, 1991, 34 (3): 257- 266

时间层	精确解	差分格式解	误差值	所需时间(s)
1	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.017160
2	1.00+e00	1.00-3.33067e-16	3.33067e-16	0.012998
3	1.00+e00	1.00-3.33067e-16	3.33067e-16	0.011783
4	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011667
5	1.00+e00	1.00-6.66134e-16	6.66134e-16	0.011951
6	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011711
7	1.00+e00	1.00-3.33067e-16	3.33067e-16	0.011630
8	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011647
9	1.00+e00	1.00-5.55112e-16	5.55112e-16	0.011787
10	1.00+e00	1.00-5.55112e-16	5.55112e-16	0.011690
11	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011579
12	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011576
13	1.00+e00	1.00-3.33067e-16	3.33067e-16	0.011611
14	1.00+e00	1.00-3.33067e-16	3.33067e-16	0.011501
15	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011609
16	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011973
17	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011524
18	1.00+e00	1.00-3.33067e-16	3.33067e-16	0.012638
19	1.00+e00	1.00-4.44089e-16	4.44089e-16	0.011606
20	1.00+e00	1.00-3.33067e-16	3.33067e-16	0.011690

[1]	陈华鑫, 贾文生. 群体博弈的逼近定理及通有收敛性[J]. 数学物理学报, 2021, 41(5): 1566-1573.
[2]	张丽红, 杨泽栋, 王国涛, Baleanu Dumitru. 一类$\bm{k}$-Hessian方程解的存在性和渐近稳定性[J]. 数学物理学报, 2021, 41(5): 1357-1371.
[3]	冯再勇, 陈宁, 台永鹏, 向峥嵘. 分数阶广义线性系统观测器设计[J]. 数学物理学报, 2021, 41(5): 1529-1544.
[4]	范东霞,赵东霞,史娜,王婷婷. 一类扩散波方程的PDP反馈控制和稳定性分析[J]. 数学物理学报, 2021, 41(4): 1088-1096.
[5]	谢亚君. 一类基于Halley-Newton型的有效修正算法[J]. 数学物理学报, 2021, 41(4): 1066-1078.
[6]	丰利香,王德芬. 具有隔离和不完全治疗的传染病模型的全局稳定性[J]. 数学物理学报, 2021, 41(4): 1235-1248.
[7]	吴斌,陈群. 一类耦合Korteweg-de Vries方程组输运系数反演问题的Lipschitz稳定性[J]. 数学物理学报, 2021, 41(3): 740-761.
[8]	刘永建,黄秋健. Rabinovich系统的Jacobi分析[J]. 数学物理学报, 2021, 41(3): 783-796.
[9]	马国栋. 强Wolfe线搜索下的修正PRP和HS共轭梯度法[J]. 数学物理学报, 2021, 41(3): 837-847.
[10]	李喜玲,高飞,李文琴. 具有免疫时滞的分数阶HBV感染模型稳定性分析[J]. 数学物理学报, 2021, 41(2): 562-576.
[11]	郭改慧,刘晓慧. 一类自催化可逆生化反应模型的Hopf分支及其稳定性[J]. 数学物理学报, 2021, 41(1): 166-177.
[12]	万升联. 解变分不等式的一种二次投影算法[J]. 数学物理学报, 2021, 41(1): 237-244.
[13]	杜丹丹,朱玉灿. K-框架和紧K-框架的算子扰动的稳定性[J]. 数学物理学报, 2021, 41(1): 29-38.
[14]	王娟,原子霞. 具有对数敏感度和混合边界的一维趋化模型解的整体存在性和收敛性[J]. 数学物理学报, 2020, 40(6): 1646-1669.
[15]	葛志昊,李瑞华. Bogoliubov-Tolmachev-Shirkov模型临界温度和能隙解的数值方法[J]. 数学物理学报, 2020, 40(6): 1699-1711.