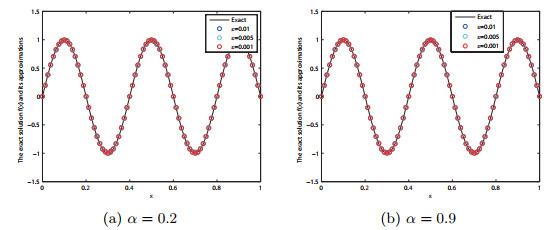
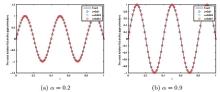
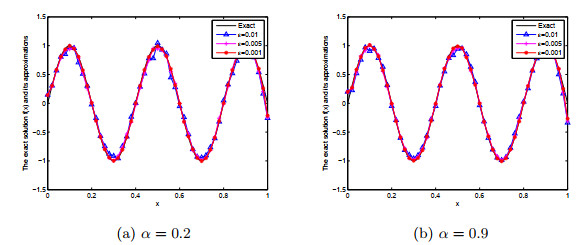
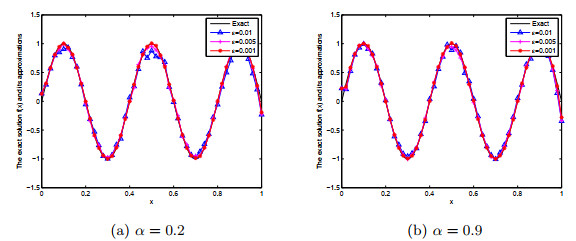
数学物理学报 ›› 2021, Vol. 41 ›› Issue (2): 427-450.
识别Rayleigh-Stokes方程源项的分数阶Landweber迭代正则化方法
- 兰州理工大学理学院 兰州 730050
-
收稿日期:2020-03-03出版日期:2021-04-26发布日期:2021-04-29 -
通讯作者:杨帆 E-mail:yfggd114@163.com;wqcfaf@163.com -
作者简介:王乾朝, E-mail:wqcfaf@163.com -
基金资助:国家自然科学基金(11961044);兰州理工大学博士基金
Fractional Landweber Iterative Regularization Method to Identify Source Term for the Rayleigh-Stokes Equation
Fan Yang*( ),Qianchao Wang(
),Qianchao Wang( ),Xiaoxiao Li
),Xiaoxiao Li
- School of Science, Lanzhou University of Technology, Lanzhou 730050
-
Received:2020-03-03Online:2021-04-26Published:2021-04-29 -
Contact:Fan Yang E-mail:yfggd114@163.com;wqcfaf@163.com -
Supported by:the NSFC(11961044);the Dr Fund of Lanzhou University of Science and Technology
摘要:
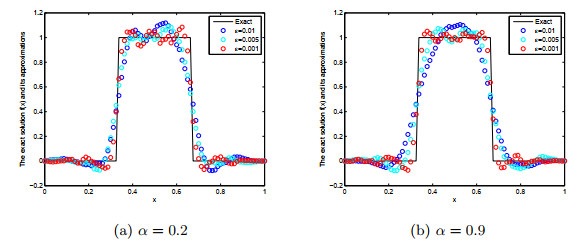
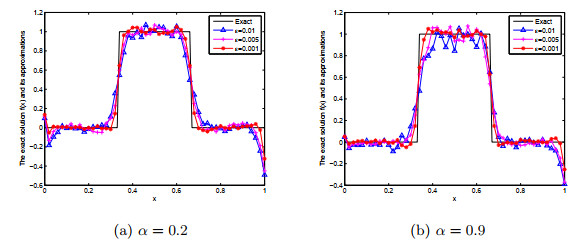
该文研究具有Riemann-Liouville时间分数阶导数的Rayleigh-Stokes方程未知源识别问题.首先证明这个问题是不适定的,并应用分数阶Landweber正则化方法求解此反问题.基于条件稳定性结果,在先验和后验正则化参数选取规则下,分别给出精确解与正则解之间的误差估计.最后通过数值例子说明此方法求解此类反问题的有效性和可行性.
中图分类号:
- O175
引用本文
杨帆,王乾朝,李晓晓. 识别Rayleigh-Stokes方程源项的分数阶Landweber迭代正则化方法[J]. 数学物理学报, 2021, 41(2): 427-450.
Fan Yang,Qianchao Wang,Xiaoxiao Li. Fractional Landweber Iterative Regularization Method to Identify Source Term for the Rayleigh-Stokes Equation[J]. Acta mathematica scientia,Series A, 2021, 41(2): 427-450.
使用本文
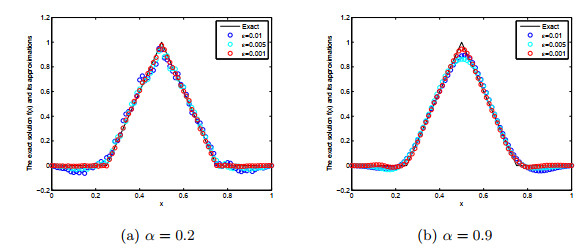
表 1
对于不同的α和ε, 例1的精确解与正则解之间的相对均方根误差"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| η(f) | ε=0.01 | Landweber | BD | 0.0099 | 0.0083 | 0.0075 |
| C-N | 0.0072 | 0.0052 | 0.0041 | |||
| 分数阶Landweber | BD | 0.0088 | 0.0076 | 0.0061 | ||
| C-N | 0.0063 | 0.0048 | 0.0039 | |||
| ε=0.005 | Landweber | BD | 0.0042 | 0.0039 | 0.0034 | |
| C-N | 0.0041 | 0.0035 | 0.0025 | |||
| 分数阶Landweber | BD | 0.0038 | 0.0035 | 0.0021 | ||
| C-N | 0.0031 | 0.0028 | 0.0011 | |||
| ε= 0.001 | Landweber | BD | 0.0025 | 0.0019 | 7.9678e-04 | |
| C-N | 0.0020 | 0.0011 | 5.5690e-04 | |||
| 分数阶Landweber | BD | 0.0018 | 0.0010 | 7.1943e-04 | ||
| C-N | 0.0011 | 8.7631e-04 | 4.6982e-04 | |||
表 2
对于不同的α和ε, 例1的精确解与正则解之间的迭代次数"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| 迭代步数(m) | ε = 0.01 | Landweber | BD | 24027 | 9658 | 30 |
| C-N | 25556 | 31634 | 37652 | |||
| 分数阶Landweber | BD | 19683 | 6514 | 21 | ||
| C-N | 21423 | 23963 | 29685 | |||
| ε = 0.005 | Landweber | BD | 46820 | 21349 | 34 | |
| C-N | 27941 | 30652 | 39541 | |||
| 分数阶Landweber | BD | 39870 | 12981 | 29 | ||
| C-N | 19685 | 23916 | 33921 | |||
| ε = 0.001 | Landweber | BD | 79686 | 38679 | 44 | |
| C-N | 35719 | 42387 | 52802 | |||
| 分数阶Landweber | BD | 68765 | 27695 | 38 | ||
| C-N | 26985 | 34796 | 44348 | |||
表 3
对于不同的α和ε, 例1的精确解与正则解之间的CPU时间"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| CPU时间(unit: s) | ε = 0.01 | Landweber | BD | 480.54 | 193.16 | 0.60 |
| C-N | 511.12 | 632.68 | 753.04 | |||
| 分数阶Landweber | BD | 393.66 | 130.28 | 0.42 | ||
| C-N | 428.46 | 479.26 | 593.70 | |||
| ε = 0.005 | Landweber | BD | 936.40 | 426.98 | 0.68 | |
| C-N | 558.82 | 613.04 | 790.82 | |||
| 分数阶Landweber | BD | 797.40 | 259.62 | 0.58 | ||
| C-N | 393.70 | 478.32 | 678.42 | |||
| ε = 0.001 | Landweber | BD | 1593.72 | 773.58 | 0.88 | |
| C-N | 714.38 | 847.74 | 1056.04 | |||
| 分数阶Landweber | BD | 1375.30 | 553.90 | 0.76 | ||
| C-N | 539.70 | 695.92 | 886.96 | |||
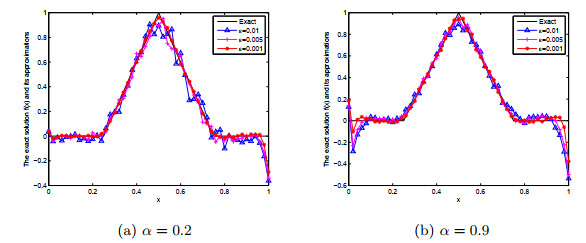
表 4
对于不同的α和ε, 例2的精确解与正则解之间的相对均方根误差"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| η(f) | ε = 0.01 | Landweber | BD | 0.0243 | 0.0128 | 0.0088 |
| C-N | 0.1039 | 0.0864 | 0.0747 | |||
| 分数阶Landweber | BD | 0.0208 | 0.0106 | 0.0075 | ||
| C-N | 0.0931 | 0.0705 | 0.0628 | |||
| ε = 0.005 | Landweber | BD | 0.0155 | 0.0116 | 0.0076 | |
| C-N | 0.0838 | 0.0725 | 0.0634 | |||
| 分数阶Landweber | BD | 0.0191 | 0.0103 | 0.0063 | ||
| C-N | 0.0786 | 0.0596 | 0.0413 | |||
| ε = 0.001 | Landweber | BD | 0.0033 | 0.0019 | 8.6476e-04 | |
| C-N | 0.0589 | 0.0362 | 0.0295 | |||
| 分数阶Landweber | BD | 0.0021 | 0.0011 | 6.5483e-04 | ||
| C-N | 0.0412 | 0.0268 | 0.0105 | |||
表 5
对于不同的α和ε, 例2的精确解与正则解之间的迭代次数"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| 迭代步数(m) | ε = 0.01 | Landweber | BD | 22348 | 6987 | 29 |
| C-N | 3717 | 5816 | 7425 | |||
| 分数阶Landweber | BD | 16534 | 3768 | 19 | ||
| C-N | 2674 | 4168 | 6123 | |||
| ε = 0.005 | Landweber | BD | 34258 | 12368 | 33 | |
| C-N | 6670 | 8126 | 11198 | |||
| 分数阶Landweber | BD | 22369 | 6879 | 26 | ||
| C-N | 4396 | 6021 | 8934 | |||
| ε = 0.001 | Landweber | BD | 79463 | 39654 | 41 | |
| C-N | 15285 | 86956 | 131965 | |||
| 分数阶Landweber | BD | 54986 | 21685 | 33 | ||
| C-N | 13210 | 69663 | 113824 | |||
表 6
对于不同的α和ε, 例2的精确解与正则解之间的CPU时间"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| CPU时间(unit: s) | ε = 0.01 | Landweber | BD | 446.96 | 139.74 | 0.58 |
| C-N | 74.34 | 116.32 | 148.50 | |||
| 分数阶Landweber | BD | 330.68 | 75.36 | 0.38 | ||
| C-N | 53.48 | 83.36 | 122.46 | |||
| ε = 0.005 | Landweber | BD | 685.16 | 247.36 | 0.66 | |
| C-N | 133.4 | 162.52 | 223.96 | |||
| 分数阶Landweber | BD | 447.38 | 137.58 | 0.52 | ||
| C-N | 87.92 | 120.42 | 178.68 | |||
| ε = 0.001 | Landweber | BD | 1589.26 | 793.08 | 0.82 | |
| C-N | 305.70 | 1739.12 | 2639.3 | |||
| 分数阶Landweber | BD | 1099.72 | 433.70 | 0.66 | ||
| C-N | 264.20 | 1393.26 | 2276.48 | |||
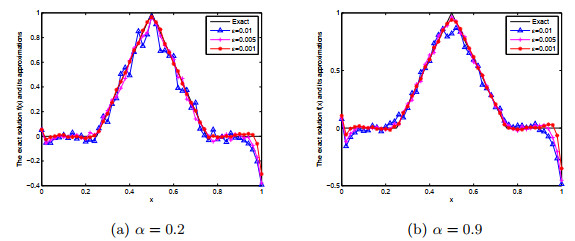
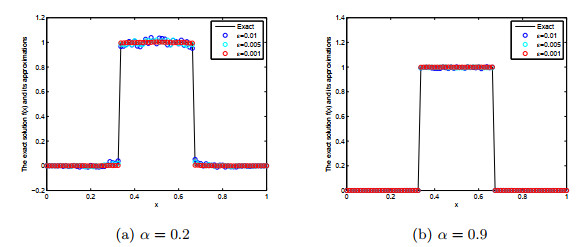
表 7
对于不同的α和ε, 例3的精确解与正则解之间的相对均方根误差"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| η(f) | ε = 0.01 | Landweber | BD | 0.0287 | 0.0196 | 0.0100 |
| C-N | 0.1867 | 0.2375 | 0.2735 | |||
| 分数阶Landweber | BD | 0.0234 | 0.0165 | 0.0008 | ||
| C-N | 0.1529 | 0.2143 | 0.2568 | |||
| ε = 0.005 | Landweber | BD | 0.0176 | 0.0102 | 0.0050 | |
| C-N | 0.1679 | 0.2139 | 0.2228 | |||
| 分数阶Landweber | BD | 0.0153 | 0.0088 | 0.0016 | ||
| C-N | 0.1428 | 0.1796 | 0.1928 | |||
| ε = 0.001 | Landweber | BD | 0.0068 | 0.0036 | 0.0010 | |
| C-N | 0.0924 | 0.1428 | 0.1522 | |||
| 分数阶Landweber | BD | 0.0053 | 0.0018 | 2.5638e-04 | ||
| C-N | 0.0723 | 0.1256 | 0.1347 | |||
表 8
对于不同的α和ε, 例3的精确解与正则解之间的迭代次数"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| 迭代步数(m) | ε = 0.01 | Landweber | BD | 47906 | 21398 | 29 |
| C-N | 4837 | 8878 | 19844 | |||
| 分数阶Landweber | BD | 31695 | 10321 | 18 | ||
| C-N | 2968 | 5367 | 16482 | |||
| ε = 0.005 | Landweber | BD | 74840 | 46709 | 33 | |
| C-N | 10244 | 168704 | 52632 | |||
| 分数阶Landweber | BD | 62390 | 30987 | 28 | ||
| C-N | 7688 | 11326 | 40986 | |||
| ε = 0.001 | Landweber | BD | 121803 | 76895 | 42 | |
| C-N | 238323 | 638825 | 788528 | |||
| 分数阶Landweber | BD | 98465 | 54326 | 37 | ||
| C-N | 196524 | 419168 | 568238 | |||
表 9
对于不同的α和ε, 例3的精确解与正则解之间的CPU时间"
| α | α = 0.2 | α = 0.5 | α = 0.9 | |||
| CPU时间(unit: s) | ε = 0.01 | Landweber | BD | 958.12 | 427.96 | 0.58 |
| C-N | 96.74 | 177.56 | 396.88 | |||
| 分数阶Landweber | BD | 639.30 | 206.42 | 0.36 | ||
| C-N | 59.36 | 107.34 | 329.64 | |||
| ε = 0.005 | Landweber | BD | 1496.80 | 934.18 | 0.66 | |
| C-N | 204.88 | 3374.08 | 1052.64 | |||
| 分数阶Landweber | BD | 1247.80 | 619.74 | 0.56 | ||
| C-N | 153.76 | 226.52 | 819.72 | |||
| ε = 0.001 | Landweber | BD | 2436.06 | 1537.90 | 0.84 | |
| C-N | 4766.46 | 12776.50 | 15770.56 | |||
| 分数阶Landweber | BD | 1969.30 | 1086.52 | 0.74 | ||
| C-N | 3930.48 | 8383.36 | 11364.76 | |||
| 1 |
Fetecau C . The Rayleigh-Stokes problem for heated second grade fluids. Int J Nonlin Mech, 2002, 37, 1011- 1015
doi: 10.1016/S0020-7462(00)00118-9 |
| 2 |
Shen F , Tan W , Zhao Y , et al. The Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative model. Nonlinear Anal Real World Appl, 2006, 7, 1072- 1080
doi: 10.1016/j.nonrwa.2005.09.007 |
| 3 |
Khan M , Anjum A , Qi H , et al. On exact solutions for some oscillating motions of a generalized Oldroyd-B fluid. Z Angew Math Phys, 2010, 61, 133- 145
doi: 10.1007/s00033-009-0004-4 |
| 4 |
Khan M . The Rayleigh-Stokes problem for an edge in a viscoelastic fluid with a fractional derivative model. Nonlinear Anal Real Word Appl, 2009, 10, 3190- 3195
doi: 10.1016/j.nonrwa.2008.10.002 |
| 5 | Chen C M , Liu F , Burrage K , et al. Numerical methods of the variable-order Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivative. J Appl Math, 2013, 204, 340- 351 |
| 6 |
Yu B , Jiang X Y , Qi H T . An inverse problem to estimate an unknown order of a Riemann-Liouville fractional derivative for a fractional Stokes' first problem for a heated generalized second grade fluid. Acta Mechanica Sinica, 2015, 31, 153- 161
doi: 10.1007/s10409-015-0408-7 |
| 7 | Zhuang P H , Liu Q X . Numerical method of Rayleigh-Stokes problem for heated generalized second grade fluid with fractional derivative. Appl Math Model, 2009, 30, 1533- 1546 |
| 8 |
Chen C M , Liu F , Burrage K , et al. Numerical methods with fourth-order spatial accuracy for variable-order nonlinear Stokes' first problem for a heated generalized second grade fluid. Comput Math Appl, 2011, 62, 971- 986
doi: 10.1016/j.camwa.2011.03.065 |
| 9 |
Wu C . Numerical solution for Stokes' first problem for a heated generalized second grade fluid with fractional derivative. Appl Numer Math, 2009, 59, 2571- 2583
doi: 10.1016/j.apnum.2009.05.009 |
| 10 |
Mohebbi A , Abbaszadeh M , Dehghan M . Compact finite difference scheme and RBF meshless approach for solving 2D Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives. Comput Methods Appl Mech Eng, 2013, 264, 163- 177
doi: 10.1016/j.cma.2013.05.012 |
| 11 |
Dehghan M , Safarpoor M , Abbaszadeh M . Two high-order numerical algorithms for solving the multi-term time fractional diffusion-wave equations. J Comput Appl Math, 2015, 290, 174- 195
doi: 10.1016/j.cam.2015.04.037 |
| 12 |
Dehghan M , Abbaszadeh M , Deng W . Fourth-order numerical method for the space time tempered fractional diffusion-wave equation. Appl Math Lett, 2017, 73, 120- 127
doi: 10.1016/j.aml.2017.04.011 |
| 13 |
Mirzaei D , Dehghan M . New implementation of MLBIE method for heat conduction analysis in functionally graded materials. Eng Anal Bound Elem, 2012, 36, 511- 519
doi: 10.1016/j.enganabound.2011.11.007 |
| 14 |
Mohebbi A , Abbaszadeh M , Dehghan M . Compact finite difference scheme and RBF meshless approach for solving 2D Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives. Comput Methcd Appl M, 2013, 264, 163- 177
doi: 10.1016/j.cma.2013.05.012 |
| 15 | Nguyen H L , Nguyen H T , Mokhtar K . Identifying initial condition of the Rayleigh-Stokes problem with random noise. Math Method Appl Sci, 2019, |
| 16 | Nguyen A L , Hoan Luu V C , Nguyen H L . Identification of source term for the Rayleigh-Stokes problem with Gaussian random noise. Math Method Appl Sci, 2018, |
| 17 |
Dehghan M . An inverse problem of finding a source parameter in a semilinear parabolic equation. Appl Math Model, 2001, 25, 743- 754
doi: 10.1016/S0307-904X(01)00010-5 |
| 18 |
Wang J , Wei T , Zhou Y . Optimal error bound and simplified Tikhonov regularization method for a backward problem for the time-fractional diffusion equation. J Comput Appl Math, 2015, 279, 277- 292
doi: 10.1016/j.cam.2014.11.026 |
| 19 |
Yang F , Li X X , Li D G , et al. The simplified Tikhonov regularization method for solving a Riesz-Feller Space-Fractional backward diffusion problem. Math Comput Sci, 2017, 11, 91- 110
doi: 10.1007/s11786-017-0292-6 |
| 20 |
Wang J G , Wei T , Zhou Y B . Tikhonov regularization method for a backward problem for the time-fractional diffusion equation. Appl Math Model, 2013, 37, 8518- 8532
doi: 10.1016/j.apm.2013.03.071 |
| 21 |
Yang F , Zhang P , Li X X , et al. Tikhonov regularization method for identifying the space-dependent source for time-fractional diffusion equation on a columnar symmetric domain. Adv Differ Equ, 2020,
doi: 10.1186/s13662-020-2542-1 |
| 22 |
Feng L X , Eldén L . Solving a Cauchy problem for a 3D elliptic PDE with variable coefficients by a quasi-boundary-value method. Inverse Probl, 2014, 30, 015005
doi: 10.1088/0266-5611/30/1/015005 |
| 23 |
Wei T , Wang J . A modified quasi-boundary value method for an inverse source problem of the time-fractional diffusion equation. Appl Numer Math, 2014, 78, 95- 111
doi: 10.1016/j.apnum.2013.12.002 |
| 24 |
Yang F , Sun Y R , Li X X , et al. , The quasi-boundary regularization value method for identifying the initial value of heat equation on a columnar symmetric domain. Numer Algor, 2019, 82, 623- 639
doi: 10.1007/s11075-018-0617-9 |
| 25 |
Yang F , Zhang Y , Liu X , Li X X . The quasi-boundary value method for identifying the initial value of the space-time an fractional diffusion equation. Acta Math Sci, 2020, 40, 641- 658
doi: 10.1007/s10473-020-0304-5 |
| 26 |
Qian A , Xiong X T , Wu Y . On a quasi-reversibility regularization method for a Cauchy problem of the Helmholtz equation. J Comput Appl Math, 2010, 233, 1969- 1979
doi: 10.1016/j.cam.2009.09.031 |
| 27 |
Yang F , Fu C L . The quasi-reversibility regularization method for identifying the unknown source for time fractional diffusion equation. Appl Math Model, 2015, 39, 1500- 1512
doi: 10.1016/j.apm.2014.08.010 |
| 28 |
Yang F , Fu J L , Li X X . A potential-free field inverse schrödinger problem: optimal error bound analysis and regularization method. Inverse Probl Sci Engin, 2020, 28, 1209- 1252
doi: 10.1080/17415977.2019.1700243 |
| 29 | Yang F , Fu J L , Li X X . A potential-free field inverse time-fractional Schrödinger problem: Optimal error bound analysis and regularization method. Math Meth Appl Sci, 2020, |
| 30 | Yang F , Fu C L , Li X X . A mollification regularization method for unknown source in time-fractional diffusion equation. Int J Comput Math, 2006, 91, 1516- 1534 |
| 31 |
Xiong X T , Fu C L , Li H F . Fourier regularization method of a sideways heat equation for determining surface heat flux. Math Anal Appl, 2006, 317, 331- 348
doi: 10.1016/j.jmaa.2005.12.010 |
| 32 |
Li X X , Lei J L , Yang F . An a posteriori Fourier regularization method for identifying the unknown source of the space-fractional diffusion equation. Inequal Appl, 2004, 2014, 1- 13
doi: 10.1186/1029-242X-2014-434 |
| 33 | Yang F , Fu C L , Li X X , et al. The Fourier regularization method for identifying the unknown source for the modified Helmholtz equation. Acta Math Sci, 2014, 34, 1040- 1047 |
| 34 |
Yang F , Ren Y P , Li X X . Landweber iteration regularization method for identifying unknown source on a columnar symmetric domain. Inverse Probl Sci Eng, 2018, 26, 1109- 1129
doi: 10.1080/17415977.2017.1384825 |
| 35 |
Yang F , Liu X , Li X X . Landweber iteration regularization method for identifying unknown source of the modified Helmholtz equation. Bound Value Probl, 2017, 2017, 1- 16
doi: 10.1186/s13661-016-0733-1 |
| 36 |
Yang F , Zhang Y , Li X X . Landweber iterative method for identifying the initial value problem of the time-space fractional diffusion-wave equation. Numer Algor, 2020, 83, 1509- 1530
doi: 10.1007/s11075-019-00734-6 |
| 37 | Yang F , Wang N , Li X X . Landweber iterative method for an inverse source problem of time-fractional diffusion-wave equation onspherically symmetric domain. J Appl Ana Comput, 2020, 10, 514- 529 |
| 38 |
Yang F , Zhang Y , Li X X , Ma C Y . Landweber iteration regularization method for identifying the initial value problem of the time-space fractional diffusion-wave equation. Advances in Difference Equations, 2017,
doi: 10.1007/s11075-019-00734-6 |
| 39 |
Yang F , Pu Q , Li X X . The fractional Landweber method for identifying the space source term problem for time-space fractional diffusion equation. Numer Algor, 2020,
doi: 10.1007/s11075-020-01006-4 |
| 40 |
Klann E , Maass P , Ramlau R . Two-step regularization methods for linear inverse problems. Inverse Ill-posed Probl, 2006, 14, 583- 607
doi: 10.1515/156939406778474523 |
| 41 |
Klann E , Ramlau R . Regularization by fractional filter methods and data smoothing. Inverse Probl, 2008, 24, 025018
doi: 10.1088/0266-5611/24/2/025018 |
| 42 |
Bazhlekova E , Jin B , Lazarov R , et al. An analysis of the Rayleigh-Stokes problem for a generalized second-grade fluid. Number Math, 2015, 131, 1- 31
doi: 10.1007/s00211-014-0685-2 |
| 43 | Engl H W , Hanke M , Neubauer A . Regularization of Inverse Problem. Boston: MA, Kluwer Academic, 1996 |
| 44 | Dehghan M , Abbaszadeh M . A finite element method for the numerical solution of Rayleigh-Stokes problem for a heated generalized second grade fluid with fractional derivatives. Eng Comput-Germany, 2017, 33, 587- 605 |
| 45 |
Yuste S B . Weighted average finite difference methods for fractional diffusion equations. J Comput Phys, 2006, 216, 264- 274
doi: 10.1016/j.jcp.2005.12.006 |
| 46 |
Irene K . A posteriori error analysis for the Crank-Nicolson method for linear Schrödinger equations. Esaim-Math Model Num, 2011, 45, 761- 778
doi: 10.1051/m2an/2010101 |
| [1] | 官声玉,吴东杰,MuratSat,杨传富. 环图上Sturm-Liouville算子的部分反谱问题[J]. 数学物理学报, 2021, 41(2): 289-295. |
| [2] | 王於平. 由内部谱数据确定的扩散算子的反问题[J]. 数学物理学报, 2013, 33(6): 1189-1195. |
| [3] | 魏莹, 戴华. 由谱数据和主子矩阵构造Jacobi矩阵及其推广[J]. 数学物理学报, 2012, 32(2): 356-363. |
| [4] | 窦以鑫, 韩波. 重构山体表面的非线性多重网格有限元反演算法[J]. 数学物理学报, 2011, 31(6): 1479-1489. |
| [5] | 莫荣华, 黎稳. 子矩阵约束下的埃尔米特广义反汉密尔顿矩阵特征值反问题及其最佳逼近[J]. 数学物理学报, 2011, 31(3): 691-701. |
| [6] | 袁永新, 戴华. 线性流形上的广义反射矩阵反问题[J]. 数学物理学报, 2009, 29(6): 1547-1560. |
| [7] | 陶有山, 边保军. 抑制剂作用下肿瘤生长模型的参数识别[J]. 数学物理学报, 2009, 29(5): 1175-1186. |
| [8] | 关力, 张忠志, 谢冬秀. 谱约束下反自反矩阵的最佳逼近问题[J]. 数学物理学报, 2009, 29(2): 316-323. |
| [9] | 龚丽莎; 胡锡炎; 张磊. 子矩阵约束下的Hermite-Hamilton矩阵反问题[J]. 数学物理学报, 2008, 28(4): 694-700. |
| [10] | 胡锡炎, 张磊, 周富照. 对称正交反对称矩阵反问题[J]. 数学物理学报, 2004, 4(5): 543-550. |
| [11] | 邱春雨, 傅初黎. 一个抛物型方程不适定问题的小波正则化方法[J]. 数学物理学报, 2002, 22(3): 361-372. |
| [12] | 李功胜, 马逸尘. 半线性热方程的源项反问题[J]. 数学物理学报, 2001, 21(2): 230-234. |
| [13] | 郝新生. 半线性波方程的一个反问题[J]. 数学物理学报, 2000, 20(zk): 602-609. |
| [14] | 郝新生 张青娥 傅初黎. 双曲型积分微分方程的一个反问题[J]. 数学物理学报, 2000, 20(3): 314-320. |
| [15] | 李功胜, 马逸尘. 热传导反问题中非线性热源的存在性[J]. 数学物理学报, 2000, 20(1): 48-57. |
| Viewed | ||||||||||||||||||||||||||||||||||||||||||||||
|
Full text 118
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
Abstract 90
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Cited |
|
|||||||||||||||||||||||||||||||||||||||||||||
| Shared | ||||||||||||||||||||||||||||||||||||||||||||||
| Discussed | ||||||||||||||||||||||||||||||||||||||||||||||
|